Codeforces 982 树边两端点计数偶数连通块 鲨鱼活动最小K最大location 扩展欧几里得方块内光线反射
A

/*Huyyt*/ #include<bits/stdc++.h> #define mem(a,b) memset(a,b,sizeof(a)) #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; const ll LLmaxn = 2e18; const int N = 100005; inline int readint() { char c = getchar(); int ans = 0; while (c < '0' || c > '9') { c = getchar(); } while (c >= '0' && c <= '9') { ans = ans * 10 + c - '0', c = getchar(); } return ans; } int main() { int n; n = readint(); string a; cin >> a; if (a.size() == 1) { if (a[0] == '0') { cout << "No" << endl; } else { cout << "Yes" << endl; } } else { if (a[0] + a[1] != '0' + '1') { cout << "No" << endl; return 0; } if (a[a.size() - 1] + a[a.size() - 2] != '0' + '1') { cout << "No" << endl; return 0; } for (int i = 1; i < a.size() - 1; i++) { if (a[i] == '0') { if (a[i - 1] == '0' && a[i + 1] == '0') { cout << "No" << endl; return 0; } } else { if (a[i - 1] == '1' || a[i + 1] == '1') { cout << "No" << endl; return 0; } } } cout<<"Yes"<<endl; } return 0; }
B

/*Huyyt*/ #include<bits/stdc++.h> #define mem(a,b) memset(a,b,sizeof(a)) #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; const ll LLmaxn = 2e18; const int N = 200005; inline int readint() { char c = getchar(); int ans = 0; while (c < '0' || c > '9') { c = getchar(); } while (c >= '0' && c <= '9') { ans = ans * 10 + c - '0', c = getchar(); } return ans; } priority_queue<pair<int, int>, vector<pair<int, int> >, less<pair<int, int> > > quemax; priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > quemin; int visit[N]; int main() { int now; pair<int, int> cnt; int n; cin >> n; for (int i = 1; i <= n; i++) { now = readint(); quemin.push(make_pair(now, i)); } string a; cin >> a; int value, aim; for (int i = 0; i < a.size(); i++) { if (a[i] == '0') { cnt=quemin.top(); quemin.pop(); cout<<cnt.second<<" "; quemax.push(cnt); } else { cnt=quemax.top(); quemax.pop(); cout<<cnt.second<<" "; } } return 0; }
C. Cut 'em all!
问你有几条边满足这条边两边的子树节点都是偶数个的
解:
当N为奇数时答案明显不存在
因为一个树的节点要不在一条边的左边 要不就在右边 所以从叶子开始往上DP 记录一个节点子树的节点数
如果节点数是偶数 那么因为节点总数是偶数 所以偶数-偶数为偶数(除了当节点数等于节点总数的情况那时候为0)
所以该点的一条边会有一个贡献

/*Huyyt*/ #include<bits/stdc++.h> #define mem(a,b) memset(a,b,sizeof(a)) #define pb push_back using namespace std; typedef long long ll; typedef unsigned long long ull; const ll LLmaxn = 2e18; const int N = 100005; inline int readint() { char c = getchar(); int ans = 0; while (c < '0' || c > '9') { c = getchar(); } while (c >= '0' && c <= '9') { ans = ans * 10 + c - '0', c = getchar(); } return ans; } vector<int> f[N]; int du[N]; int ans[N]; int n; int u, v; int aim; int number = 0; int getans(int x, int pre) { ans[x] = 1; int len = f[x].size(); if (len == 1 && x != aim) { return ans[x]; } for (int i = 0; i < len; i++) { int to = f[x][i]; if (to == pre) { continue; } getans(to, x); ans[x] += ans[to]; } if(ans[x]%2==0&&ans[x]!=n) number++; return ans[x]; } int main() { n = readint(); if (n % 2) { cout << -1 << endl; return 0; } for (int i = 1; i <= n - 1; i++) { u = readint(), v = readint(); f[u].push_back(v); f[v].push_back(u); du[u]++, du[v]++; } for (int i = 1; i <= n; i++) { if (du[i] == 1) { aim = i; getans(i, -1); break; } } cout<<number<<endl; return 0; }
D. Shark
给你N个数字的一个数列 每个数字表示鲨鱼在第i天活动的距离
假设鲨鱼活动的距离小于K则不会移动location 不小于则移动 (移动是单方向的 不会回去)
问你找一个最小的K使得location的数量最大且同时鲨鱼在每个location的天数相同
解:
其实就是用带大小的并查集找一个数 使得比他小的数在原数列中相连的为一块 要求块内数的数量一样且块的数量尽量多
先用一个num数组表示数 另一个数组index表示下标 然后用num给index从小到大排序 再遍历从而保证数的出现是从小到大的
sum[i]表示 以第 i 位置及其旁边不大于它的连续的数的集合大小 而cntsum[i]表示大小为i的集合有几个
每次遍历一个位置如果它两边有比它小的数就用并查集把它俩并起来 同时维护好并查集的大小
如果碰到num[aim+1]!=num[aim]或者到头i==n的情况 同时满足该并查集大小*并查集内元素数目等于现在遍历到的总数目 就是合法的 尝试更新答案

/* Huyyt */ #include <bits/stdc++.h> #define mem(a,b) memset(a,b,sizeof(a)) #define mkp(a,b) make_pair(a,b) #define pb push_back const int dir[8][2] = {{0, 1}, {1, 0}, {0, -1}, { -1, 0}, {1, 1}, {1, -1}, { -1, -1}, { -1, 1}}; using namespace std; typedef long long ll; inline int readint() { char c = getchar(); int ans = 0; while (c < '0' || c > '9') { c = getchar(); } while (c >= '0' && c <= '9') { ans = ans * 10 + c - '0', c = getchar(); } return ans; } const long long mod = 1e9 + 7; const int N = 1e5 + 5; int n; int ansnum = 0; int ans; int num[N]; int index[N]; int father[N]; int sum[N]; int cntsum[N]; bool cmp(int x, int y) { return num[x] < num[y]; } int findfather(int x) { if (father[x] != x) { return findfather(father[x]); } return x; } void merge(int x, int y) { x = findfather(x); y = findfather(y); if (!y) //保证合并的数是不大于num[aim]的数 { return ; } cntsum[sum[x]]--, cntsum[sum[y]]--; sum[x] += sum[y]; father[y] = x; cntsum[sum[x]]++; } int main() { n = readint(); for (int i = 1; i <= n; i++) { num[i] = readint(); index[i] = i; } sort(index + 1, index + 1 + n, cmp); int value, aim; int now = 0; for (int i = 1; i <= n; i++) { aim = index[i]; father[aim] = aim; now++; sum[aim] = 1; cntsum[1]++; merge(aim, aim - 1), merge(aim, aim + 1); //尝试合并旁边的数 if ((i == n || num[aim + 1] != num[aim]) && now == cntsum[sum[findfather(aim)]]*sum[findfather(aim)]) { if (cntsum[sum[findfather(aim)]] > ansnum) { ansnum = cntsum[sum[findfather(aim)]]; ans = num[aim] + 1; } } } cout << ans << endl; return 0; }
E
Exgcd:对于非负的两个整数a,b 一定存在整数 n,m 使得 a*n+b*m=gcd(a,b)
给你一个N*M的方块 一个点 一个方向向量(与边界平行或者成45度) 点碰到方块边界是完全弹性碰撞
问你这个点朝这个方向运动最后会不会落入四个角会的话落入哪个角
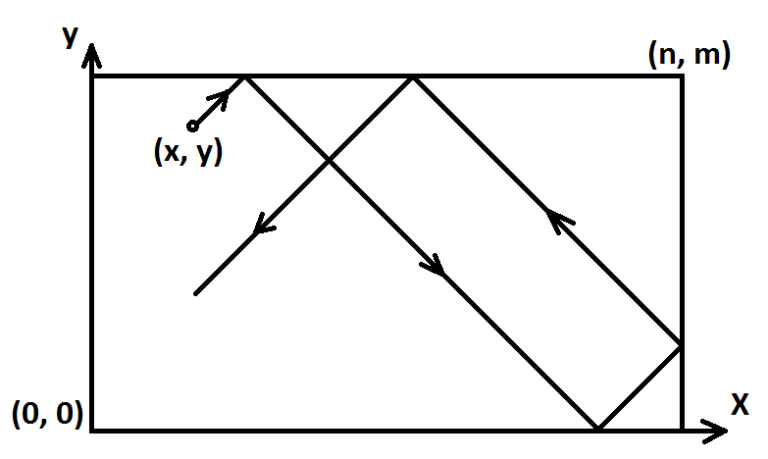
转载自:https://www.cnblogs.com/zhouzhendong/p/9055728.html
解:
画一组数据
5 3 4 0 1 1
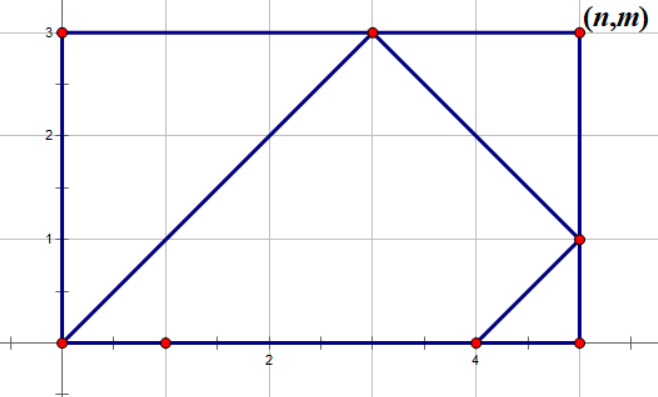
通过对称,画成这样
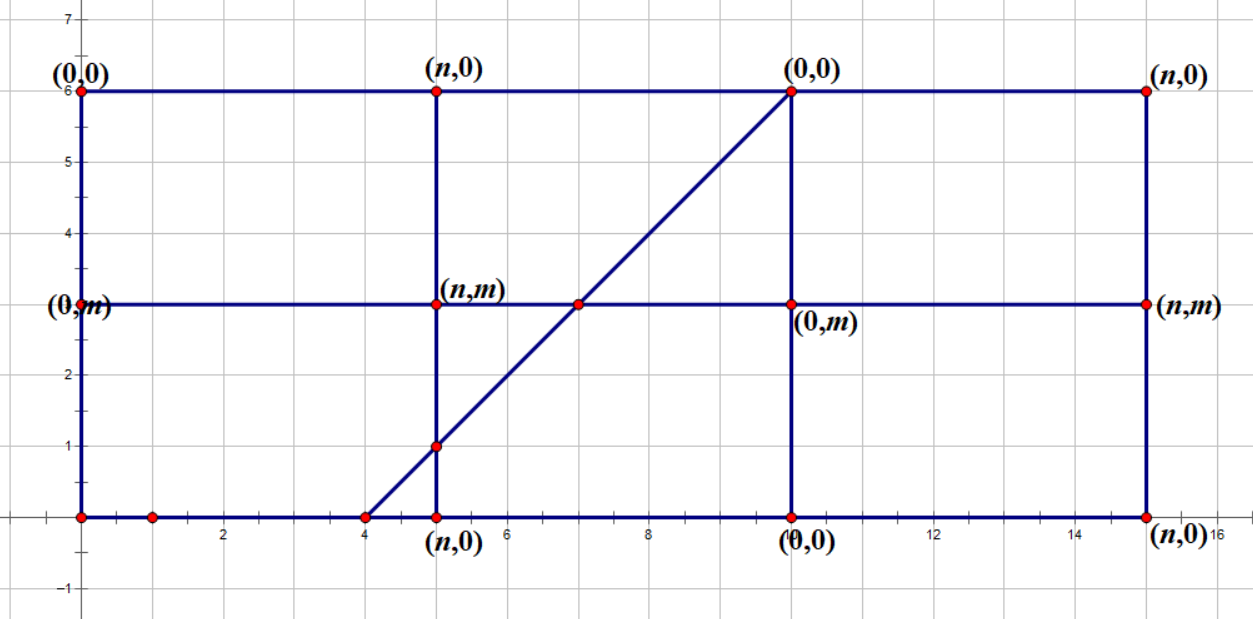
然后问题就大致变成了求直线到达的第一个满足n|Tx m|Ty的点(Tx,Ty)
为了方便,我们再把原图画成这样:
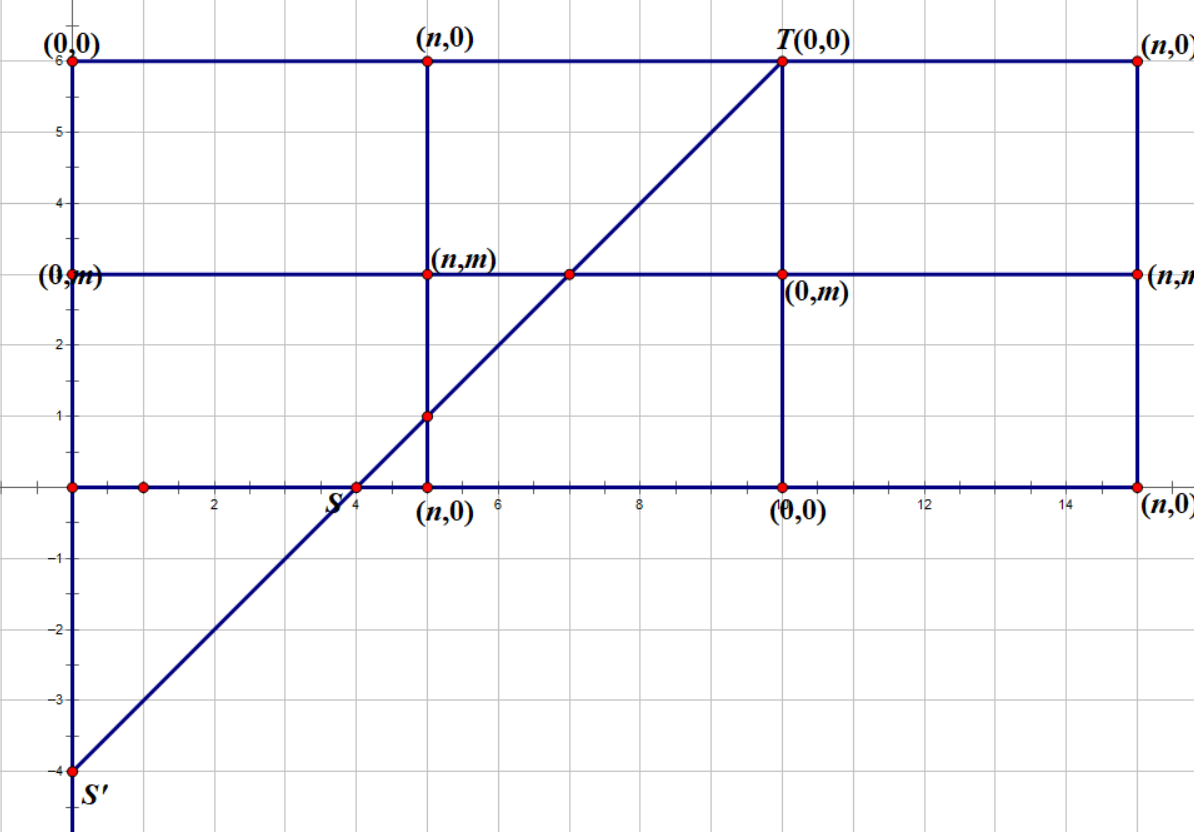



 浙公网安备 33010602011771号
浙公网安备 33010602011771号