欧拉降幂公式 Super A^B mod C

Description

Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).

Input

There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.

Output

For each testcase, output an integer, denotes the result of A^B mod C.

 

降幂公式: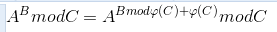

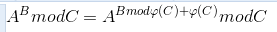
//计算欧拉函数O(sqrt(n))
ll Phi(ll x)
{
        ll i;
        ll re = x;
        for (i = 2; i * i <= x; i++)
                if (x % i == 0)
                {
                        re /= i;
                        re *= i - 1;
                        while (x % i == 0)
                        {
                                x /= i;
                        }
                }
        if (x ^ 1)
        {
                re /= x, re *= x - 1;
        }
        return re;
}
ll Quick_Power(ll x, ll y, ll p)
{
        ll re = 1;
        while (y)
        {
                if (y & 1)
                {
                        (re *= x) %= p;
                }
                (x *= x) %= p;
                y >>= 1;
        }
        return re;
}
int Solve(int p)
{
        if (p == 1)
        {
                return 0;
        }
        int phi_p = Phi(p);
        return Quick_Power(2, Solve(phi_p) + phi_p, p);
}
int T, n, a, c;
string b;
int main()
{
        ios_base::sync_with_stdio(false);
        //    freopen("data.txt","r",stdin);
        while (cin >> a >> b >> c)
        {
                int phi_c = Phi(c);
                ll sum = 0;
                for (int i = 0; i < b.size(); i++)
                {
                        sum = (sum * 10 + b[i] - '0') % (phi_c);
                }
                cout << Quick_Power(a, sum + phi_c, c) << endl;
        }
}