P1361 小M的作物 最小割理解

如果没有组合效益的存在 我们直接每个点两部分的最大值即可

换成网络流模型来看 即把S点看作是A田 把T点看作是B田 每种作物看作一个点 分别连边(S,i,A[i]) (i,T,B[i])

最后图中所有边权和减去最大流即为答案.这个很好理解,因为最小割=最大流,一种作物只能选择A,B里的一个 

所以对于每个点必要删去一条边,删去的边相当于我们不要的选项 剩下的和S,T相连的边相当于我们的选择 此时删去的肯定是最小的边.

接下来我们要处理组合效应的问题.

每个组合效应有三种选择:A/B/无

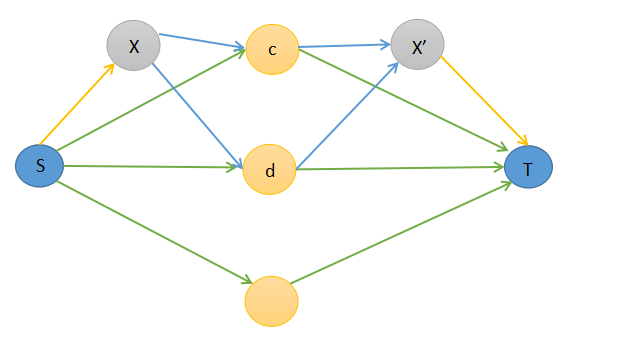
这样对于每个组合只建一个点很难满足要求 则我们把每个组合拆成A,B两个点  A点和S建边(S,A,C1[i])  B点和T建边(B,T,C2[i]) 表示选择A,B能得到的贡献.

再对于组合里的每个数都连边(A,K[i],INF) (K[i],B,INF) 这样图中除边权为INF的边的边权减去跑出来的最大流即为答案.

为什么这样跑出来即是我们选择要删去的选项？

因为最小割不可能会割INF的边

每个组合效应的A点 他旗下的每个点要都选A他才能产生贡献,如果有一个选了B则会产生增广路径,那么就必须要割掉(S,A,C1[i])

每个组合效应的B点 他旗下的每个点要都选B他才能产生贡献,如果有一个选了A则同样会产生增广路径,必须要割掉(B,T,C2[i])

#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N=3010;
const int M=2000100;
const int inf=0x3f3f3f3f;
int head[N],edge[M],to[M],next[M],cnt=1;
void add(int u,int v,int w)
{
    to[++cnt]=v;next[cnt]=head[u];edge[cnt]=w;head[u]=cnt;
    to[++cnt]=u;next[cnt]=head[v];edge[cnt]=0;head[v]=cnt;
}
int dep[N],used[N],pre[N],tot,s[N],ans,m,n,sum;
queue <int > q;
bool bfs()
{
    while(!q.empty()) q.pop();
    q.push(0);
    memset(dep,0,sizeof(dep));
    dep[0]=1;
    while(!q.empty()&&q.front()!=n+1)
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=next[i])
        {
            int v=to[i],w=edge[i];
            if(!dep[v]&&w)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    return !q.empty();
}
int main()
{
    scanf("%d",&n);
    int w,v,k,c1,c2;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&w);
        sum+=w;
        add(0,i,w);
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&w);
        sum+=w;
        add(i,n+1,w);
    }
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&k,&c1,&c2);
        add(0,i+n+1,c1);sum+=c1;
        add(i+n+m+1,n+1,c2);sum+=c2;
        for(int j=1;j<=k;j++)
        {
            scanf("%d",&v);
            add(i+n+1,v,inf);
            add(v,i+n+m+1,inf);
        }
    }
    while(bfs())
    {
        memset(used,0,sizeof(used));
        s[++tot]=0;
        while(tot)
        {
            int u=s[tot];
            if(u==n+1)
            {
                int mi=inf,id;
                for(int i=tot;i>1;i--)
                    if(mi>=edge[pre[s[i]]])
                    {
                        mi=edge[pre[s[i]]];
                        id=i;
                    }
                ans+=mi;
                for(int i=tot;i>1;i--)
                {
                    edge[pre[s[i]]]-=mi;
                    edge[pre[s[i]]^1]+=mi;
                }
                tot=id-1;
                used[n+1]=0;
            }
            else
            {
                for(int i=head[u];i;i=next[i])
                {
                    int v=to[i],w=edge[i];
                    if(!used[v]&&dep[v]==dep[u]+1&&w)
                    {
                        used[v]=1;
                        s[++tot]=v;
                        pre[v]=i;
                        break;
                    }
                }
                if(u==s[tot]) tot--;
            }
        }
    }
    printf("%d\n",sum-ans);
    return 0;
}