BZOJ 1006 完美消除序列&最大势算法&弦图

　　K国是一个热衷三角形的国度,连人的交往也只喜欢三角原则.他们认为三角关系:即AB相互认识,BC相互认识,CA相互认识,是简洁高效的.为了巩固三角关系,K国禁止四边关系,五边关系等等的存在.所谓N边关系,是指N个人 A1A2...An之间仅存在N对认识关系:(A1A2)(A2A3)...(AnA1),而没有其它认识关系.比如四边关系指ABCD四个人 AB,BC,CD,DA相互认识,而AC,BD不认识.全民比赛时,为了防止做弊，规定任意一对相互认识的人不得在一队，国王想知道最少可以分多少支队。

 

子图:V'为V的子集 E'为E的子集

诱导子图:对于V' 只要在G中有边 那么在G'中同样应该有边

 

最大独立集:最大的一个点的子集使任何两个点不相邻——最大独立集数

最大团:点数最多的团——团数

最小染色:用最少的颜色给点染色使相邻点颜色不同——色数

最小团覆盖:用最少个数的团覆盖所有的点——最小团覆盖数

结论:  团数<=色数  最大独立集数<=最小团覆盖数 

 

弦(Chord):连接环中不相邻的两个点的边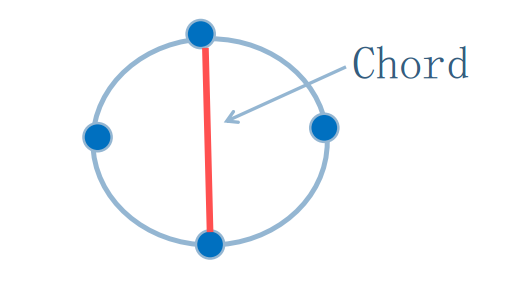

弦图:一个无向图称为弦图，当图中任意长度大于3的环都至少有一个弦

弦图的每一个诱导子图一定是弦图

弦图的判断:

ZJU1015

给定一个无向图，判定它是否为弦图

单纯点:设N(v)为与点v相邻的点的点集 一个点是单纯点当且仅当{v}+N(v)的诱导子图为一个团

引理:任何一个弦图都至少有一个单纯点  不是完全图的弦图至少有两个不相邻的单纯点

完美消除序列:

一个点的序列(每个点出现且恰好出现一次)V1,V2....Vn满足Vi在{Vi,Vi+1,Vn}的诱导子图中为一个单纯点

定理:一个无向图是弦图当且仅当它有一个完美消除序列

MCS算法O(n+m):

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <queue>
  4 #include <cstdlib>
  5 #define N 10000 + 10
  6 #define M 2000000 + 10
  7  
  8 using namespace std;
  9  
 10 struct edge
 11 {
 12     int to, next;
 13 }e[M];
 14 int n, m, num, ans, maxs;
 15 int p[N], seq[N], col[N], lab[N], flag[N];
 16 struct node
 17 {
 18     int now;
 19     node *next;
 20 }f[N];//链表
 21 void add(int x, int y)
 22 {
 23     e[++num].to = y;
 24     e[num].next = p[x];
 25     p[x] = num;
 26 }
 27 void put(int x)
 28 {
 29     node *po = (struct node *)malloc(sizeof(struct node));
 30     po->next = f[lab[x]].next;
 31     po->now = x;
 32     f[lab[x]].next = po;
 33 }//链表的插入
 34 void read(int &x)
 35 {
 36     x = 0;
 37     char c = getchar();
 38     while(c < '0' || c > '9') c = getchar();
 39     while(c >= '0' && c <= '9')
 40     {
 41         x = (x << 1) + (x << 3) + c - '0';
 42         c = getchar();
 43     }
 44 }
 45 void init()
 46 {
 47     int x, y;
 48     read(n), read(m);
 49     for (int i = 1; i <= m; ++i)
 50     {
 51         read(x), read(y);
 52         if (x == y) continue;
 53         add(x, y);
 54         add(y, x);
 55     }
 56 }
 57 void create()
 58 {
 59     for (int i = 1; i <= n; ++i)
 60     f[i].next = NULL;//
 61     for (int i = 1; i <= n; ++i) put(i);
 62     maxs = 0;//初始化
 63     for (int i = n; i; i--)//用逆序求
 64     {
 65         node *po = f[maxs].next;//找到当前最大
 66         while(flag[po->now])
 67         {
 68             f[maxs].next = po = po->next;//及时删除没有用的点（漏掉的话会超时）
 69             while(po == NULL)
 70             {
 71                 maxs--;
 72                 po = f[maxs].next;
 73             }
 74         }
 75         f[maxs].next = po->next;//更新
 76         while(f[maxs].next == NULL) maxs--;
 77         int x = po->now;
 78         flag[x] = 1, seq[i] = x;
 79         for (int j = p[x]; j; j = e[j].next)
 80         if (!flag[e[j].to])
 81         {
 82             ++lab[e[j].to];//加势
 83             if (lab[e[j].to] > maxs) maxs = lab[e[j].to];
 84             put(e[j].to);
 85         }
 86     }
 87 }
 88 void paint()
 89 {
 90     for (int i = 1; i <= n; ++i)
 91     flag[i] = -1;
 92     for (int i = n; i; i--)
 93     {
 94         int x = seq[i];
 95         for (int j = p[x]; j; j = e[j].next)
 96         flag[col[e[j].to]] = i;
 97         for (int j = 1; j <= n; ++j)
 98         if (flag[j] != i)
 99         {
100             col[x] = j;
101             break;
102         }
103         if (ans < col[x]) ans = col[x];
104     }
105 }
106 void deal()
107 {
108     create();
109     paint();
110     printf("%d\n", ans);
111 }
112 int main()
113 {
114     //freopen("kingdom.in", "r", stdin);
115     //freopen("kingdom.out", "w", stdout);
116     init();
117     deal();
118     return 0;
119 }
BZOJ 1006

 

 

 

posted @ 2018-12-02 16:18  Aragaki  阅读(504)  评论(0)  编辑  收藏  举报