力扣 题目72- 编辑距离

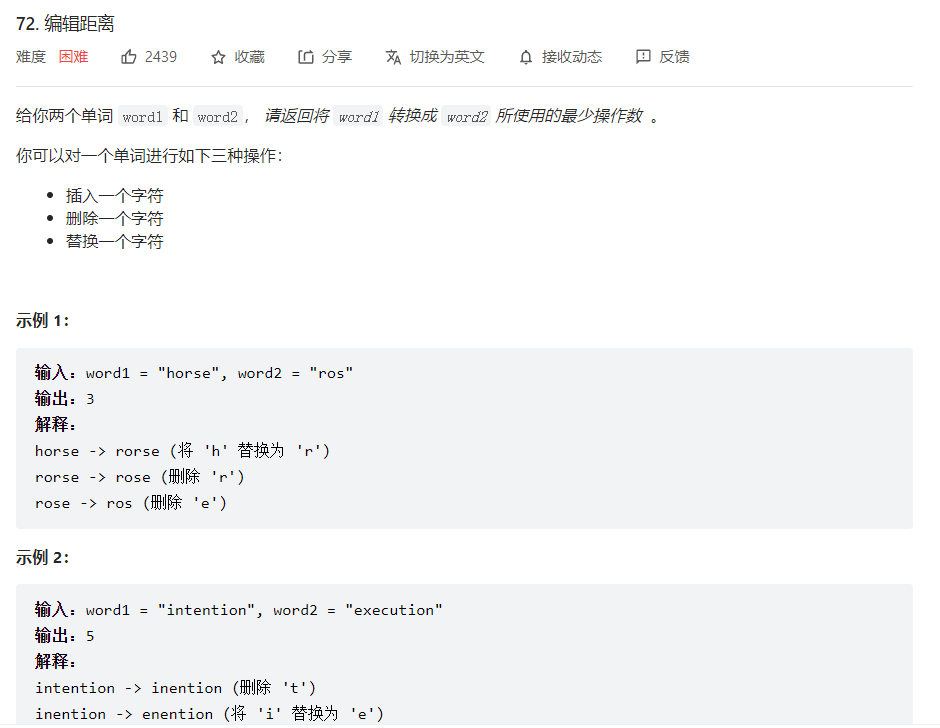
题目

题解(评论区大佬解法)

首先很明显这题需要使用动态规划法 关键在于 在word1遍历到当前字符时如何利用前面的已经遍历过字符的最少操作数 成为了难题

题目这样 写到

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

 那么我们按照这样划分为4种情况(这里的i 与 j 是相等数值的 指双方遍历到同样位置  与代码中的i/j加以区分)

需要插入

     假如 word1[0..i] 到 word2[0..j-1] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换就是k+1 只要在k步后word1插入word2[i]即可

 

需要删除

    假如 word1[0..i-1] 到 word2[0..j] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换就是k+1 只要在k步后word1删除word1[i]即可

需要替换

    假如 word1[0..i-1] 到 word2[0..j-1] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换就是k+1 word1[i]和word2[i]不相等 只要在k步后word1[i]替换word2[i]即可

不变

    假如 word1[0..i-1] 到 word2[0..j-1] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换就是k word1[i]和word2[i]相等 

可以看出我们可以同时遍历双方字符串 然后根据上面四种情况找到最小值 这样每一轮的最小就是整体的最小 由于不变肯定是最小步骤操作 所以如果可以word1[i]和word2[i]相等 直接使用k

题目

#include<iostream>
#include<string>
#include<vector>
using namespace std;

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.length();
        int n = word2.length();

        vector<vector<int>> cost(m + 1, vector<int>(n + 1));
        //双方有一个为长度0 结果肯定为 有长度的字符串的长度(只要不断添加/删除即可)
        for (int i = 0; i <= m; ++i) {
            cost[i][0] = i;
        }
        for (int j = 0; j <= n; ++j) {
            cost[0][j] = j;
        }
        //从word1的第一个字符开始遍历
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                //相等
                if (word1[i - 1] == word2[j - 1]) {
                    cost[i][j] = cost[i - 1][j - 1];
                }
                else {
                    //1+k(cost[i - 1][j - 1]->替换 cost[i][j - 1]->添加 cost[i - 1][j]->删除)
                    cost[i][j] = 1 + min(cost[i - 1][j - 1], min(cost[i][j - 1], cost[i - 1][j]));
                }
            }
        }
        return cost[m][n];
    }
};

int main() {
    Solution sol;
    string word1 = "horse";
    string word2 = "ros";
    int result=sol.minDistance(word1, word2);
    cout << result << endl;
}