力扣 题目42--接雨水

题目

---

题解

1.题目的思路

看见这个题 有点和力扣 题目11- 盛最多水的容器 有点相似 那么我们能不能也用左右指针的方法去做呢？

但是题目要求都不一样 那么左右指针应该代表比较合适呢？

我们可以发现 如下图 

当left指向mid的左边最大值

当right指向mid的右边最大值 时

 无论是横向计算还是纵向计算都比较有利 但是由于横向计算要考虑重复的情况

所以我们使用纵向 即计算mid位置上有多少格子符合 然后加和

如上图 现在是1 即height[left]-height[mid]=2-1;

如上图 现在是2 即height[left]-height[mid]=2-0;

 

如上图 现在是1 即height[left]-height[mid]=2-1;

那么反过来呢？

如上图 现在是1 即height[right]-height[mid]=2-1;

也就是说min(height[left],height[right])-height[mid]

2.最大值的思路

我们可以直接遍历左边然后再遍历右边 然后if什么的找到最大值 但是这样显示有点麻烦

那么记录一下之前的最大值情况

//找到position位置的左边最大

 

即 左边的最大值变成left[position] = max(left[position - 1], height[position - 1]);

//找到n- position-1位置的右边最大

右边的最大值变成right[n- position-1] = max(right[n - position], height[n - position]);

也就是说我们只需要将新加的数height[position - 1]与position-1的左边最大值left[position - 1]比较 就能知道 position的左边最大值了

右边虽然同理 但是需要反向循环即从右到左 才能和左边一样比较

3.递归

这里我采用了递归方法 而力扣评论区的老哥使用了普通的方法 如果不理解递归的话可以去看看

代码

#include<iostream>
#include<vector>
#include <algorithm>
using namespace std;
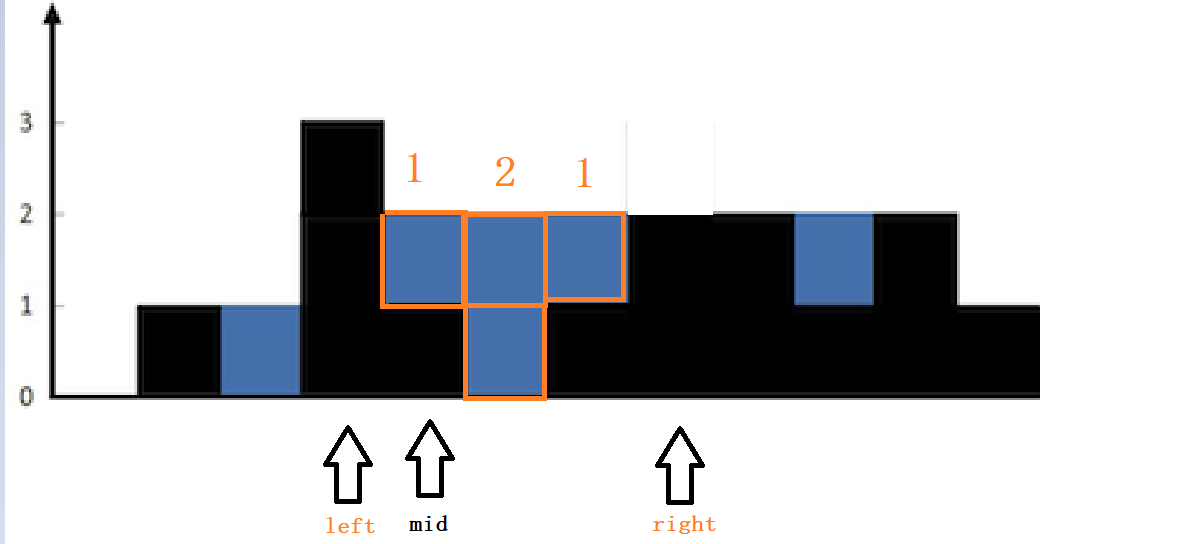
int looktrap(vector<int>& height,int position,int &add, vector<int> &left, vector<int>& right,int n) {
    //当n==1 即只有一个数字时或者position == n - 1 说明已经到头 开始读取
    if (n==1||position == n - 1) {
        //循环
        for (int i = 0; i < n; i++) {
            //比较左边最大和右边最大哪个小
            int level = min(left[i], right[i]);
            add += max(0, level - height[i]);
        }
        return add;
    }
    //找到position位置的左边最大
    left[position] = max(left[position - 1], height[position - 1]);
    //找到n- position-1位置的右边最大
    right[n- position-1] = max(right[n - position], height[n - position]);
    //递归
    add=looktrap(height, position+1, add,left,right,n);
    return add;
}

class Solution {
public:
    int trap(vector<int>& height) {
        //add一开始为0
        int add = 0;
        ////n是height的长度
        int n = height.size();
        //存放左边与右边的最大值
        vector<int> left(n), right(n);
        //调用递归
        looktrap(height, 1, add, left, right,n);
        return add;
    }
};

int main() {
    Solution sol;
    vector<int> height = { 1 };
    int num=sol.trap(height);
    cout << num << endl;;
}