POJ 1067 取石子游戏
题意:有两堆个数分别为a和b的石子,两个人轮流取石子,一次可以取一堆中任意个数的石子,或者在两堆中取相同个数的石子,最先没有石子可以取的人输,你先取,赢为1输为0。
解法:威佐夫博弈。看完题先找规律,能推理出前几个必败态有1 2, 3 5, 4 7, 6 10……从必败态可以一步达到的状态一定是必胜态,所以在找规律中发现,在必败态的a或b上加若干数,或a和b同时加若干数,就会转化为必胜态,所以下一个必败态不可能会有一个数量和之前的必败态相同,所以下一个必败态的a就是在之前的必败态内没出现过的第一个整数,而对于必败态a和b同时加若干数就转化为必胜态的情况,前一个必败态的a和b的差设为k,那么下一个必败态的差为k + 1时就不会转化为必胜态了,所以得出an和bn的求法,但这题的数据范围太大,不能将所有必败态求出,在这里用到了贝亚蒂定理:
在数论中,贝亚蒂定理(英文:Beatty sequence)指:若
使得
。定义集(贝亚蒂列)
,则P 和 Q 构成正整数集的一个分划:
,
。
即是说:若两个正无理数的倒数之和是1,则任何正整数都可刚好以一种形式表示为不大于其中一个无理数的正整数倍的最大整数。
此定理由Sam Beatty在1926年发现。
——维基百科
通过之前的描述,数列an和bn符合贝亚蒂数列,即两者没有交集,且并集为正整数集。
由贝亚蒂定理可知,an = [np], bn = [nq], 且bn = an + n, 所以bn = np + n = n(p + 1),即q = p + 1,解方程1 / p + 1 / (p + 1) = 1得p = (1 + sqrt(5)) / 2。
所以当给出a和b(a < b)时, n = b - a,若(1 + sqrt(5)) / 2 × n等于a,则说明为必败态。
代码:
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string>
#include<string.h>
#include<math.h>
#include<limits.h>
#include<time.h>
#include<stdlib.h>
#include<map>
#include<queue>
#include<set>
#include<stack>
#include<vector>
#define LL long long
using namespace std;
int main()
{
int a, b;
while(~scanf("%d%d", &a, &b))
{
if(a > b)
{
int tmp = a;
a = b;
b = tmp;
}
int n = b - a;
if((int)((1 + sqrt(5.0)) * 0.5 * n) == a)
{
puts("0");
}
else
puts("1");
}
return 0;
}



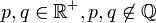 使得
使得 。定义集(贝亚蒂列)
。定义集(贝亚蒂列)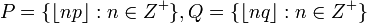 ,则P 和 Q 构成正整数集的一个分划:
,则P 和 Q 构成正整数集的一个分划: ,
, 。
。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号