思维/人类智慧题乱做
GYM102154C Quick sort
一眼看起来相当不可做,但是思考一下,直接排序是 \(O(n)\) 的,要做的实际上只是把某个数移动到某个位置。
从前往后把数字 \(i\) 移动到位置 \(i\),但是题目给的排序方式是向后移动的,怎么办呢?时间倒流,逆变换即将第 \(k+1\) 个数移动到第 \(1\) 个。
感性上这样非常优,分析一下可知期望复杂度是 \(\sum \log n-\log (n-len)=O(n)\)。
然而这是期望复杂度,还是会被出题人卡掉,怎么办呢?我们发现题目的排序方式相当的随机,所以在输入时先对 \(p\) 胡乱做几次排序,就达到了随机打乱(Random Shuffle)的目的了。
ABC238F Cubic? (2300)
先把 \(\leq \sqrt n\) 的判掉,剩下的都是 \(1\) 或者质数,只需要判断区间内每个质数是否出现次数都整除 \(3\) 即可。
用三进制不进位加法(三进制异或),好像会被卡但是没被卡。
时间复杂度 \(O(n+q)\)。
ARC122E Increasing LCMs (2500)
从全局入手,考虑 \(A_k\) 能被放在最后的必要条件为:
于是可以 \(O(n^2 \log A_i)\) 找出所有这样的 \(k\)。
结论:若有解,则在所有这样的 \(k\) 中,任意一个放在最后都有解。
证明:考虑证明对于任意 \(x \neq y\),若 \(A_y\) 填在最后有解,则 \(A_x\) 填在最后也有解。具体而言,将 \(A_x\) 移到倒数第二个位置,再与 \(A_y\) 互换。那么前面的位置仍然合法(限制变松了),而 \(A_x,A_y\) 也仍然合法(因为它们在全局都合法)。
故不断确定最后一位,时间复杂度 \(O(n^3 \log A_i)\)。
PTZ Winter 2020 Day 5 F The Halfwitters
显然要么不 \(\text{rand}\),只要 \(\text{rand}\) 一次无论初始情况如何都变成一样了。
设 \(f_P\) 表示状态 \(P\) 只使用前两种操作的最小代价。显然第二种操作至多使用 \(1\) 次(否则删掉两次情况不变),于是若 \(P\) 的逆序对数量为 \(t\),则:
设 \(g\) 为 \(\text{rand}\) 一次后最优策略的期望时间,则:
注意到 \(f_P\) 只有 \(O(n^2)\) 种取值,排序后枚举 \(f_i \neq g \neq f_{i+1}\) 可以解出 \(g\)。
解出 \(g\) 后原问题的答案即为 \(\min\{f_P,C+g\}\)。
逆序对数量可以预处理,总时间复杂度 \(O(n^4+qn^2)\)。
ARC118C Coprime Set (1200)
注意到全部 \(\gcd\) 不为 \(1\) 的限制,故不能直接将所有数定为 \(2t(t \in [1,5000])\)。
考虑将所有数分为三组,使得任意两组内 \(\gcd\) 均不为 \(1\)。第一组形如 \(6t(t \in [1,1666])\),第二组形如 \(10t(t \in [1,1000] \wedge 3 \nmid t)\),第三组形如 \(15t(t \in [1,666] \wedge 2 \nmid t)\)。
可以构造出 \(n=1666+1000+666-2 \times 333=2666 \geq 2500\)。
ARC131D AtArcher (2300)
注意到一定存在最优解满足任意相邻两支箭的距离为 \(D\),否则经调整不劣。
将数轴从原点分成左右两半,两边箭的数量绝对值之差不超过 \(1\)。不妨只考虑右半边并设箭的数量为 \(\lfloor \dfrac{n}{2} \rfloor\),只要对所有 \(t\) 算出第一支箭在 \(t \in (0,D]\) 时的分数即可 \(O(D)\) 组合出答案。
枚举每一段 \([l,r)\)(注意 \(\lfloor \dfrac{n}{2} \rfloor\) 支箭的限制)对 \(t\) 的贡献,发现贡献只有 \(3\) 段,差分优化区间加即可。
总时间复杂度 \(O(M+D)\)。
CF1685D1/2 Permutation Weight (2800/3500)
令 \(mp=p^{-1}\),即 \(mp_{p_i}=i\),则原式改写为:
可以理解为将 \(n\) 个二元组 \((i,mp_i)\) 排成一个环,代价即在二元组间跳转的距离之和。
将 \(p\)(或 \(mp\))视为一个置换,将每个循环节染上一种颜色,感性理解应该尽可能在同种颜色间跳转(即尽可能使 \(mp_{q_i}=q_{i+1}\))。设共有 \(k\) 种颜色。
考虑在连边 \((mp_{q_i},q_{i+1})\),则每个点恰有一条入边与一条出边,故形成一些环。注意到大小为 \(m\) 的环的贡献至少为 \(2(m-1)\),取等当且仅当环的点编号连续且可以被拆分为单增及单减的两条链。
为了能遍历到整张图,还要求若将每种颜色的点分别缩起来并将边看作无向边,则所有颜色必须联通。
大小为 \(m\) 的环至多能减少 \(m-1\) 个颜色联通块,而总共减少了 \(k-1\) 个颜色联通块,说明 \(\sum\limits_i (m_i-1) \geq k-1\),故答案有下界 \(2(k-1)\)。
事实上这个下界可以达到,当且仅当:
-
每个点恰有一条入边与一条出边。(合法性)
-
所有环使得所有颜色相互联通。(合法性)
-
每个环的点编号连续且可以被拆分为单增及单减的两条链。(最优性)
-
每个环不会重复合并某两种颜色。(最优性)
对于 Easy Version,只需考虑每个 \(i \in [1,n)\),若 \(col_i \neq col_{i+1}\) 且这两种颜色未被合并就将这两个点合并,最后将所有合并出的区间变成环即可。
对于 Hard Version,按字典序尝试加入每条边,只需要判断目前加入的边是否能够构造出合法解即可。
注意到已经连出的边只可能是环,单增链或单减链,故可以这样判断:
-
不存在两条单增链相交,不存在两条单减链相交(自环同时算作单增链及单减链)。
-
不存在未连边的点同时被单增链及单减链覆盖。
-
目前连的边没有重复合并某两种颜色。具体而言,对所有若 \(col_i \neq col_{i+1}\) 且 \((i,i+1)\) 被某条边覆盖的 \(i\) 连边 \((col_i,col_{i+1})\),判断是否成环即可。
-
剩下的边可能使所有颜色联通。具体而言,对所有 \(i\) 不为某个环的右端点且 \(i+1\) 不为某个环的左端点的 \(i\) 连边 \((col_i,col_{i+1})\),判断是否联通即可。
总时间复杂度 \(O(n^3)\)。
CF1672I PermutationForces (3000)
PermutationForces /fn
把排列看作 \(n\) 个二维平面上的点 \((i,p_i)\),那么每次操作相当于删去一个点,将它左上方,右下方及左上方的的点分别向下方,左方,左下方平移。
假设答案为 \(m\)。注意到操作不会改变点的相对位置:
-
对于一个 \(|x_i-y_i| \leq m\) 的点,无论如何操作其始终保持 \(|x_i-y_i| \leq m\)。
-
对于一个 \(|x_i-y_i| > m\) 的点,无论如何操作其 \(|x_i-y_i|\) 不会增加。
这意味着操作顺序不会影响合法性,直接每次贪心取最小的 \(|x_i-y_i|\) 删去是正确的。
直接去优化需要支持矩形减及单点查,大概可以用数据结构(如树套树)做到 \(O(n \log^2 n)\)。
瓶颈在于矩形修改,考虑让点具有单调性,这样就可以让矩形修改变为区间修改。
首先将绝对值拆开,注意到直线 \(y=x\) 两侧的点不会跨越,将这两侧的点分开维护。下面以 \(y>x\) 的点为例。
注意到对于 \((x_i,y_i)\),若存在 \(j\) 使 \(x_j>x_i,y_j<y_i\),那么 \((x_j,y_j)\) 始终比 \((x_i,y_i)\) 更优。
于是暂时不考虑 \((x_i,y_i)\),只维护按 \(x\) 排序后 \(y\) 的后缀最小值,称这些点为关键点。
于是关键点的 \(y\) 单调递减,矩形修改就变为了区间修改。每次修改只会修改另一侧的点(因为左上角没有关键点),需要线段树二分出修改范围。
在每次删除点后还需要找出新产生的关键点,可以用 set 维护关键点集合以找到被删除的点的后继 \(u\),再不断在线段树上二分出最后一个 \(y_i<y_u\) 的 \(i\) 作为关键点。总点数为 \(n\),故该部分总复杂度为 \(O(n \log n)\)。
最后还需要计算新产生的关键点现在的权值,即计算在其右下方的已经被删除的点数量。由于已经被删除的点都在其下方,可以用 在其下方的已经被删除的点数量 减去 在其左方的已经被删除的点数量。容易用树状数组维护。
于是只需要维护六棵线段树(一棵维护非关键点,两棵维护关键点,其中一棵用于二分修改范围),两个树状数组和两个 set 即可。总时间复杂度 \(O(n \log n)\)。
ARC135D Add to Square (2800)
考虑矩阵 \(A\) 能变换到什么样的矩阵 \(B\)。
结论:\(A\) 能变换到 \(B\) 当且仅当 \(\forall i \in [1,n],\sum\limits_{j=1}^m (-1)^{i+j} a_{i,j}=\sum\limits_{j=1}^m (-1)^{i+j} b_{i,j}\) 且 \(\forall j \in [1,m],\sum\limits_{i=1}^n (-1)^{i+j} a_{i,j}=\sum\limits_{i=1}^n (-1)^{i+j} b_{i,j}\)。
证明: 必要性:显然每次操作不会改变每行及每列的交替和。
充分性:可以用至多 \((n-1)(m-1)\) 次操作使 \(a_{1,1},a_{1,2},\cdots,a_{n-1,m-1}\) 和 \(b_{1,1},b_{1,2},\cdots,b_{n-1,m-1}\) 相等。由于每行每列的交替和相等,故剩下的值也是相等的。
记 \(x_i=\sum\limits_{j=1}^m (-1)^{i+j} a_{i,j},y_j=\sum\limits_{i=1}^n (-1)^{i+j} a_{i,j}\),于是问题变为构造矩阵 \(B\) 使得每行和为 \(x_i\),每列和为 \(y_j\) 且所有数绝对值之和最小。
考虑向全零矩阵内依次填数来到达目标状态。那么令 \(b_{i,j} \leftarrow b_{i,j}+x\) 等价于令 \(x_i \leftarrow x_i+k,y_j \leftarrow y_j+k\),并花费 \(|k|\) 的代价。
称这样一次操作为 \((i,j,x)\),那么问题变为用最小的代价通过操作得到目标的 \(x,y\) 数组。又由于操作可逆,问题也等价于用最小的代价通过操作将 \(x,y\) 数组变为全零数组。
结论:代价最小值为 \(\max(\sum\limits_{i=1}^n |x_i|,\sum\limits_{j=1}^m |y_j|)\)。
显然这是下界,下面给出一种构造方式。
-
若存在 \(x_i<0,y_j<0\),进行操作 \((i,j,1)\)。归纳可知代价是正确的。
-
若存在 \(x_i>0,y_j>0\),进行操作 \((i,j,-1)\)。归纳可知代价是正确的。
若以上两个条件都不满足,说明当前的 \(x,y\) 中至少有一个为全零(注意 \(x,y\) 数组和是相同的,故不存在全正与全负的情况)。不妨设 \(x\) 为全零,对 \(y\) 进行操作:
- 若存在 \(y_i<0,y_j>0\),进行操作 \((1,i,1),(1,j,-1)\)。归纳可知代价是正确的。
操作次数不超过 \(O(nm)\) 次。粗略实现容易做到 \(O((n+m)nm)\),足以通过。精细实现可以做到 \(O(nm)\)。
ARC141F Well-defined Abbreviation (4100)
数竞证明题 + AC 自动机好题
(思路)
脑洞一下为了使终止状态唯一,需要什么条件。
考虑两种操作 \(T_A,T_B\),设删去的字符串分别为 \(S_i,S_j\):
-
若它们删去的字符串不重叠,那么相当于是同一种操作,不需要处理。
-
若它们删去的字符串重叠,说明 \(S_i\) 的某段后缀等于 \(S_j\) 的某段前缀。那么我们希望删去后结果一样,即 \(S_i=A+B,S_j=B+A\)。
违背第二种情况的反例即存在 \(S_i,S_j\) 使 \(S_i=A+B,S_j=B+C\) 且 \(A \neq C\)。我们希望这种反例下一定存在坏串。
考虑串 \(A+B+C\) 可以删成 \(A\) 和 \(C\),那么只要 \(A\) 和 \(C\) 的终止状态不一样,\(A+B+C\) 就是坏串了。
接下来构造更强的一个条件:\(A\) 和 \(C\) 不能被操作,也即对于任意 \(i \neq j\),\(S_i\) 不包含 \(S_j\)。
对于每个 \(S_i\),不断删去 \(S_j(j \neq i)\),得到某一个终止状态:
-
若该终止状态是空串,说明 \(S_i\) 可以被其它 \(S_j\) 所代替。直接将 \(S_i\) 删去。
-
若该终止状态不是空串,而另一个终止状态是空串(直接删掉 \(S_i\)),那么 \(S_i\) 就是一个坏串。
这样处理后,要么已经找到了坏串,要么剩下的串满足 对于任意 \(i \neq j\),\(S_i\) 不包含 \(S_j\)。
结论:不存在坏串当且仅当不存在 \(S_i,S_j\) 使 \(S_i=A+B,S_j=B+C\) 且 \(A \neq C\)。
证明:
必要性:由于不存在 \(t \neq i\) 使 \(S_i\) 包含 \(S_t\),也不存在 \(t \neq i\) 使 \(A\) 包含 \(S_t\),故 \(A\) 无法被操作;同理 \(C\) 也无法被操作。故 \(A\) 和 \(C\) 已经是两个不同的终止状态,故 \(A+B+C\) 是坏串。
充分性:反证。设最短的坏串为 \(S\),那么 \(S\) 能到达的状态的终止状态唯一(否则与 \(S\) 是最短矛盾)。设操作 \(T_A \neq T_B\) 使 \(T_AS\) 的终止状态 \(X\) 与 \(T_BS\) 的终止状态 \(Y\) 不一样。讨论两类情况均可得到矛盾:
-
若 \(T_A\) 与 \(T_B\) 删去的字符串不重叠,那么 \(T_AT_BS=T_BT_AS\);而前者的终止状态为 \(X\),后者的终止状态为 \(Y\)。故 \(T_AT_BS\) 是更短的坏串,矛盾。
-
若 \(T_A\) 与 \(T_B\) 删去的字符串重叠,设 \(T_A=A+B\),\(T_B=B+C\),那么由假设 \(A=C\)。故 \(T_A=T_B\),与前提矛盾。
于是,只需要实现:
-
对于每个 \(S_i\),不断从其中删去 \(S_j(j \neq i)\),判断是否能删空。
-
判断是否存在 \(S_i,S_j\) 使 \(S_i=A+B,S_j=B+C\) 且 \(A \neq C\)。
对于第一部分,对所有串建出 AC 自动机,对每个点处理出其 fail 树祖先上的某一个终止节点。
对每个串 \(S_i\) 依次加入每个字符,如果跑到某个终止节点 fail 树的子树内,那么就与某个 \(S_j\) 匹配上了,回退 \(len_j\) 步继续做即可。
对于第二部分,仍然对所有串建出 AC 自动机,对每个点处理出其 fail 树子树内的某一个终止节点。
先处理出 \(f_{i,t}(t \leq len_i)\) 表示若 \(B\) 为 \(S_i\) 长为 \(t\) 的后缀,可以匹配到的某一个 \(j\)。
对每个串 \(S_i\),先把整个串放到自动机上跑一遍跑到 \(x\) 节点,再从 \(x\) 不断跳 fail 指针统计即可。这是因为 fail 指针的意义即 树上存在的节点中该串的最长后缀。
最后对于每个 \(j=f_{i,t}\),若不满足 \(len_j=len_i\) 且 \(f_{j,len_i-t}=i\),那么就找到了一个坏串。(容易发现若存在坏串,那么 \(f_{i,t}\) 只记录一个 \(j\) 一定足以找到坏串)
总时间复杂度 \(O(|\sum| \cdot \sum |S_i|)\),常数略大。
ARC145E Adjacent XOR (3600)
差分不好处理。时间倒流,改为从 \(B\) 变成 \(A\),每次操作是作前缀和。
考虑 \(B\) 能通过操作变到怎样的 \(A\)。
结论:\(B\) 能变成 \(A\) 当且仅当对所有 \(i \in[1,n]\),存在 \(S_i \in \{1,2,\cdots,i-1\}\) 使 \(a_i=b_i \oplus (\oplus_{t \in S_i} b_t)\)。
证明:
必要性:显然 \(a_i\) 不可能被 \(b_j(j>i)\) 贡献到,而 \(b_i\) 对 \(a_i\) 的贡献必然是 \(1\)。
充分性:对 \(n\) 归纳构造。当 \(n=1\) 时显然成立。若 \(n-1\) 成立:
-
若 \(n-1 \in S_n\),那么由归纳假设令 \(S_j=\varnothing(j<n-1),S_{n-1}=\{1,2,\cdots,n-1\} \setminus S_n\)(前缀和操作不改变线性基,所以这是可以做到的),再对 \(n\) 做一次操作即可。
-
若 \(n-1 \notin S_n\),那么由归纳假设令 \(S_j=\varnothing(j<n-1),S_{n-1}=S_n\),对 \(n\) 做一次操作;再令 \(S_j=\varnothing(j<n)\),对 \(n\) 做一次操作即可。
这样 \(b_n=a_n\)。最后由归纳假设,前 \(n-1\) 个数也可以复原,故对 \(n\) 也成立。
下面给出一种在 \(n \log W\) 步内的构造方案。
与证明中不同,从后往前构造(这样就不会影响已经构造好的数)。设 \(b_{i+1},b_{i+2},\cdots,b_n\) 已经构造好,现在需要使 \(b_i=a_i\)。
由于不能影响后面的数,不能对后面的数进行操作。那么最后一步一定是对 \(i\) 进行操作。那么这一步之前需要满足 \(b_1 \oplus b_2 \oplus \cdots \oplus b_i = a_i\)。记 \(s=b_1 \oplus b_2 \oplus \cdots \oplus b_{i-1}\),下面考虑如何操作使 \(s\) 变为 \(b_i \oplus a_i\)。
考虑 \(B_t\) 表示 \(b_1,b_2,\cdots,b_t\) 构成的线性基,若 \(B_{t-1}\) 的秩与 \(B_t\) 的秩不同,称 \(t\) 是特殊点。那么前 \(t\) 个数中的特殊点的值实际上就是 \(B_t\) 的一组基底。注意到操作是不会改变线性基的,故特殊点也不会改变。
设 \(t\) 是特殊点,注意到若对 \(t+1\) 操作,则对 \(s\) 的贡献是 \(b_t\) 及某些 \(t\) 前面的特殊点的值(\(t\) 后面的特殊点没有贡献)。
那么就可以利用 \(B_i\) 来凑出 \(s\) 了。倒序遍历 \(i\) 前面的所有特殊点 \(t\),设 \(s\) 还需要异或上 \(\Delta=s \oplus b_i \oplus a_i\),那么若 \(\Delta\) 在 \(B_i\) 中含有 \(b_t\) 这一维,就对 \(t+1\) 操作。
那么对于每个 \(i\) 至多需要 \(\log W\) 次操作,总操作次数不超过 \(n\log W\),时间复杂度 \(O(n \log^2 W)\)。
ARC130F Replace by Average (3200)
发现如果没有下取整,那么所求就是 \(n\) 个点所构成的下凸壳。可以用单调队列求出。
然而下取整会让某些点降低,从而让更多的点降低。
会发现最后的形态形如两根斜率均为整数的线段(如图红色部分):
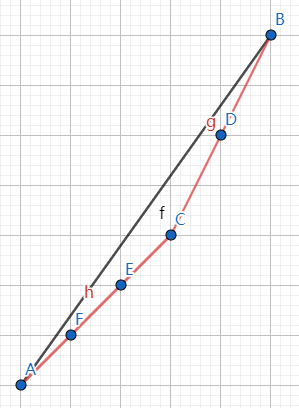
显然其不能再操作了。
同时设原线段的斜率为 \(k\),这两根线段的斜率为 \(k_1<k_2\),有 \(k_2=k_1+1\) 且 \(k_1 \leq k \leq k_2\)。
但这样仍然不够,原因是 \(k_1\) 相同的线段间可能还可以继续操作(如图蓝色部分):
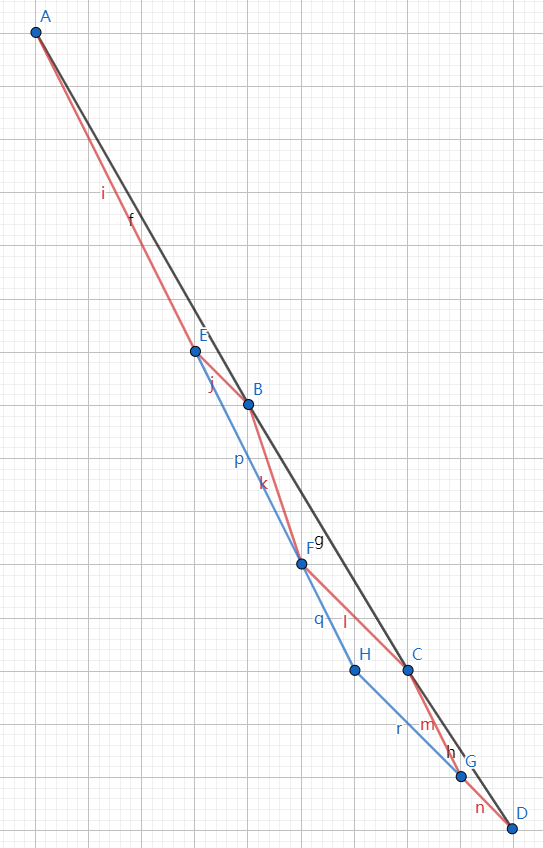
那么将 \(k_1\) 相同的线段连续段合并即可。
时间复杂度 \(O(n)\)。
ARC034F SS (3400)
这题和 P7525 Shelter 什么关系
记 \(S\) 的最长 Border 为 \(B(S)\)。
设字符串 \(S\) 长度不超过一半的 Border 为 \(T\),则 \(f(S)=(S-T)^2\)。
由于 \(S\) 都是平方串,设 \(S'\) 表示 \(S\) 的前一半,那么 \(T=B(S')\),且 \(f(S)=(S'+S'-T)^2\)。
记 \(g(S)=S+S-B(S)\)。接下来考虑 \(f_0=S'-B(S'),f_1=S'\),\(f_k=g(f_{k-1})(k>1)\)。手玩一下就会发现:
结论:当 \(S'\) 为整循环串时,设其最小循环节为 \(P\) 且 \(S=X^t\),则 \(f_k=X^{t+k-1}(k \geq 1)\);否则,当 \(k \geq 2\) 时有 \(f_k=f_{k-1}+f_{k-2}(*)\) 且 \(f_{k-2}=B(f_{k})(**)\)。
证明:前者显然(一定有 \(f_k-B(f_k)=X\),否则 \(X\) 不是最小的循环节)。后者归纳证明:
-
当 \(k=2\) 时,\(f_2=S'+S'-B(S')=f_1+f_0\),故 \((*)\) 对 \(k=2\) 成立。
-
若 \((**)\) 对 \(k\) 成立,那么 \(f_{k-2}=B(f_k)\),故 \(f_{k+1}=f_k+f_k-B(f_k)=f_k+f_{k-1}\),\((*)\) 对 \(k+1\) 成立。
-
若 \((*)\) 对 \(\leq k+1\) 成立,那么 \(f_{k+1}=f_k+f_{k-1}=f_{k-1}+f_{k-2}+f_{k-1}\),\(f_{k-1}\) 是 \(f_{k+1}\) 的 Border。假设 \(f_{k+1}\) 有更长的 Border \(P\):
-
若 \(|P| > |f_k|\),说明 \(f_{k+1}\) 有短于 \(f_{k-1}\) 的周期,那么 \(f_{k}\) 也有短于 \(f_{k-1}\) 的周期,即 \(f_k\) 有长于 \(f_{k-2}\) 的 Border。但由归纳假设 \(f_{k-2}\) 是 \(f_k\) 的最长 Border,矛盾。
-
若 \(|P| \leq |f_k|\),则设 \(d=|P|-|f_{k-1}|\),\(P=f_{k-1}+A=B+f_{k-1}\),其中 \(A,B\) 分别为 \(f_{k-2}\) 长为 \(d\) 的前缀和后缀。由于 \(f_{k-2}\) 是 \(f_{k-1}\) 的前缀,故 \(A\) 也是 \(f_{k-1}\) 的前缀,即 \(A\) 是 \(P\) 的长为 \(d\) 的 Border;又 \(f_{k-1}\) 也是 \(P\) 的 Border,由弱周期引理得 \(P\) 有长为 \(\gcd(d,|f_{k-1}|)\) 的周期。
由于 \(d \leq |f_{k-2}| < |f_{k-1}|\),故 \(f_{k-1}\) 是整循环串。设 \(f_{k-1}\) 的最小循环节是 \(X\) 且 \(f_{k-1}=X^t(t>1)\),则 \(f_k=X^{t+1}\),\(f_{k+1}=X^{t+2}\)。
如果 \(k=1\),已经与前提矛盾;否则,与归纳假设 \(f_{k+1}=f_{k}+f_{k-1}\) 矛盾。
-
-
故 \((**)\) 对 \(k+1\) 成立。
得到结论后就简单了。
当 \(S'\) 是整循环串时,所求串 \(f^{\infty}(S)=X^{\infty}\)。
当 \(S'\) 不是整循环串时,串长 \(|f_k|\) 呈指数级增长。暴力处理出前 \(\log r\) 个 \(f_k\) 及所含字母数量,将 \(f^{\infty}(S)\) 的前缀拆成若干 \(f_k\) 之和,统计即可。
时间复杂度 \(O(|\sum| \log r)\)。
ARC123F Insert Addition (3400)
吐槽:这题的错解是真的离谱,网上搜了三篇全叉掉了,AT 里一页 AC 代码只有三分之一没被叉,而且似乎大部分人写的代码都是 \(O(n \sqrt n \log n)\) 的。
将每个数表示成 \(bx+ay\) 的形式。那么初始为 \((0,1),(1,0)\),每次操作即在相邻两个二元组间插入它们的和。
容易发现这就是 Stern-Brocot 树,因此考虑到的每个二元组都可看作一个最简分数。
题意要求的是 Stern-Brocot 树的第 \(n\) 层,其一定含有分子分母都小于等于 \(n\) 的所有最简分数;还可能含有其它分数,但题意限制了 \(bx+ay \leq n\),故所有分子或分母大于 \(n\) 的分数都不需要考虑。
那么问题变为求在 \(bx+ay \leq n\) 的范围内,将所有 \(x,y\) 互质的整点按 \(y/x\) 升序排序后第 \(L \sim R\) 个整点。
先考虑求出第 \(L\) 大的整点,需要二分斜率,那么可以考虑:
-
直接二分实数。暴力可以这样写,但如果要用类欧需要转换成分数,容易炸精度。
-
在 Stern-Brocot 树上二分,复杂度多一个 \(\log\) 但是可以保证值域在 \(n\) 以内。注意直接跑复杂度是错的,深度可能达到 \(n\),需要每次倍增向下跳的度数。
考虑怎么求出 \(y \leq cx\) 且 \(bx+ay \leq n\) 的所有 \(x,y\) 互质的整点个数 \(f(n)\)。记 \(g(n)\) 为该范围内的整点个数,则有:
由于范围是两条直线与坐标轴围出的,可以用类欧在 \(O(\log n)\) 的时间内算出 \(g(n)\)。
预处理出 \(\lfloor \dfrac{n}{t} \rfloor\) 的莫比乌斯函数前缀和(可以用杜教筛优化)后可以整除分块计算。
该部分总时间复杂度 \(O(n^{2/3}+\sqrt n \log^3 n)\)。
接下来考虑求出了 \(L\) 的答案 \(x\),如何求出剩下的 \(R-L\) 个数。
在 Stern-Brocot 树上类似二叉搜索树上不断找后继即可。即分别 DFS 左子树与右子树,遍历完子树后就往父亲跳,当然还要不断维护与 \(x\) 的大小关系。
容易发现除了 \(x\) 的祖先中父亲在左边的之外,每一次遍历都能获得一个答案。由于深度不超过 \(n\),浪费的步数也不超过 \(n\),那么搜索的复杂度不超过 \(O(n+R-L)\)。
总时间复杂度 \(O(n+\sqrt n \log^3 n)\)。
AGC047E Product Simulation (3000)
若 \(A=B=0\) 则无论怎样操作都只能得到 \(0\),故一定正确。
先把 \(1\) 造出来:\([A+B>0]=1\)。那么就可以造出 \(2^k\)。
考虑 \(A,B \leq 1\) 怎么做:\(A \cdot B=[A=1 \wedge B=1]=[A+B>1]\)。
考虑 \(B \leq 1\) 怎么做:倍增用 \(B\) 凑出 \(A\)。维护一个初始为 \(0\) 的变量 \(s\),从大到小枚举每个 \(2^k\),设 \(p=[s+2^k<A+1]\),令 \(s \leftarrow s+B \cdot p \cdot 2^k\),那么最后 \(s\) 即为答案。
考虑原问题怎么做:还是倍增用 \(B\) 凑出 \(A\)。维护初始为 \(0\) 的变量 \(s,t\),从大到小枚举每个 \(2^k\),设 \(p=[t+2^k<A+1]\),令 \(t \leftarrow t+p \cdot 2^k,s \leftarrow s+B \cdot p \cdot 2^k\),那么最后 \(s\) 即为答案。
操作步数 \(O(\log^3 W)\),实测约 \(36000\) 步。
将 \(A,B\) 拆成二进制位再相乘可以做到 \(O(\log^2 W)\)。
AGC043E Topology (3500)
神仙构造题
容易发现 \(\forall T \subseteq S,a_T \geq a_S\) 是有解的必要条件,下面通过构造说明它也是充分条件。
称满足 \(a_S=0\) 且 \(\forall T \subsetneq S, a_T=1\) 的 \(S\) 为关键状态。只要满足所有关键状态的要求(本身不可行,删去任何一个点后可行),方案就是合法的。
那么先考虑对一个关键状态如何构造,最后全部首尾相连即可。
一个点容易构造,但两个点呢?

对于 \(n\) 更大的情况,考虑不断向左边加入新点类似归纳构造。为了方便构造,将环的最左边开个口:

(上图套住 \(1 \sim n-1\) 的黑环与红环都是归纳构造的)
上图给出了删去 \(1 \sim n-1\) 中某个点的情况。容易验证删去 \(n\) 同样也能完全解开。
例如,\(n=3\) 时构造出的环长这样:

如果所有点是连着的,那么操作步数是 \(T(n)=2T(n-1)+7\),实测 \(n=8\) 时用了 \(1528\) 步,步数限制应该是绰绰有余。
部分图片来自博客 AT5802 [AGC043E] Topology - 约瑟夫用脑玩。
AGC003D Anticube (2600)
记值域 \(V=10^{10}\)。
将所有限制关系连边,即求最大独立集大小。
边集会形成若干完全二分图,这是因为对每个数 \(s_i\) 求出其最大立方因子 \(x\),令 \(t_i=s_i/x\),那么与 \(s_i\) 连边的数 \(s_j\) 对应的 \(t_j\) 与 \(t_i\) 一一对应。于是在每个二分图中贪心选点数较多的一部点即可。
现在问题变成如何对每个数分解质因数。注意到如果 \(s_i\) 有连边,必须满足:
-
没有 \(>\sqrt{V}\) 的质因子 \(p\),否则 \(s_j\) 中至少有 \(p^2>V\)。
-
\(> \sqrt[3]{V}\) 的质因子至多只有一种,否则若有两种 \(p,q\),那么 \(s_j\) 中至少有 \(p^2q^2>V\)。
那么暴力除掉 \(\leq \sqrt[3]{V}\) 的质因子,再判断一下是否是质数或质数的平方即可。
时间复杂度 \(O(n \dfrac{\sqrt[3]{V}}{\log V})\)。
CF1142E Pink Floyd (3200)
先考虑没有粉色边的情况。将所有点加入候选点集(所有可能成为答案的点),重复进行以下步骤直到点集只剩一个点 \(rt\):
- 选择两个点 \(u,v\),询问它们间边的方向。设 \(u \rightarrow v\),则将 \(v\) 从点集中删去。
那么问出的边形成一棵以 \(rt\) 为根的外向树,故 \(rt\) 即为答案。
回到原题,问题在于粉色边相连的点间不能询问。
考虑对所有粉色边求强连通分量并缩点,将所有入度为零的强连通分量加入集合,重复进行以下步骤直到集合只剩一个强连通分量:
- 选择两个强连通分量 \(x,y\),从中任选两个未被删去的点,询问它们间边的方向。设 \(u \rightarrow v\) 且 \(u \in x,v \in y\),则将 \(v\) 删去。若 \(y\) 被删空,则将 \(y\) 从集合中删去并将新产生入度为零的强连通分量加入集合。
最后一个强连通分量里的点一定可以通过绿色边到达未被删除的点,通过粉色边到达剩下的点。
时间复杂度 \(O(n+m)\)。
ABC275Ex Monster (3200)
注意到若对区间 \((l,r)\) 操作且 \(\min(B_{l-1},B_{r+1}) \leq \max\{B_l,B_{l+1},\cdots,B_r\}\),那么将区间扩大一定不劣。
故对 \(\{B_i\}\) 序列建出大根堆笛卡尔树,那么存在最优解使得每一次操作都对笛卡尔树上的一个区间操作,
限制即对于每一个笛卡尔树上的区间 \((l,r,x)\)(\(x\) 为区间内最大值下标),它的祖先的操作次数不少于 \(A_x\)。
直接贪心从上往下尽可能少的操作显然是错的,因为祖先节点额外的操作有可能能减少更多子孙节点的操作。
考虑 DP,设 \(f_{u,x}\) 表示对于节点 \(u\) 的祖先已经操作了 \(x\) 次,其子树中最少的操作次数。转移即:
设 \(F_u(x)=f_{u,x}\),那么每个 \(F_u(x)\) 均为分段一次函数。考虑维护该分段函数的断点及斜率变化量以及 \(F_u(0)\),转移分三步:
- \(F_u(x)=B_u x+\sum\limits_v F_v(x)\)。
- \(F_u(x) \leftarrow \min\limits_{t \geq A_u} \{F_u(t)\}\)。
- \(F_u(x) \leftarrow F_u(x)-B_u x\)。
容易发现叶子处的函数是下凸的(斜率单调不降),而每步转移都不改变函数的凸性。故第二步转移相当于将 \(A_u\) 前的部分以及斜率小于 \(0\) 的部分抬高削平,即删去断点的一段前缀。
用左偏树维护上述信息,时间复杂度 \(O(n \log n)\)。

