CF/其它 计数乱做

CF1515E Phoenix and Computers (2200)

最后一定是若干段全都手动打开的电脑，每一段中间有一台自动开启的电脑。

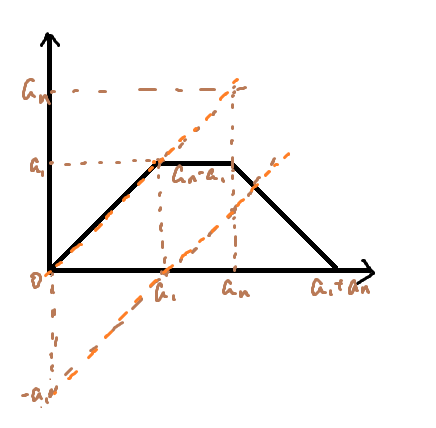
将 一台自动开启-一段手动开启 视作一整段，则长度为 $l$ 的一段方案数是 $2^{n-2}$（先随意开启一台电脑，之后只能选择向左或向右拓展）。

写成生成函数后二项式展开即可，时间复杂度 $O(n^2)$。（式子不见了）

CF1621G Weighted Increasing Subsequences (3200)

考虑对每一个元素 $a_i$ 计算贡献。

设 $x$ 为最后一个大于 $a_i$ 的 $a$ 下标，则符合条件的上升序列可以分为两段：$[1,i]$ 中以 $i$ 为结尾的上升子序列 及 $[i,x)$ 中以 $i$ 为开头的上升子序列。

前者很好算，后者则是 $[i,n]$ 中以 $i$ 为开头的上升子序列个数 减去 $[i,x]$ 中以 $i$ 为开头，$x$ 为结尾的上升子序列个数。

考虑枚举每一个 $x$。符合条件的 $x$ 一定满足其等于后缀 $\max$。那么对应的 $i$ 一定在这个 $x$ 到下一个 $x$ 之间，直接抽取出来做即可。

时间复杂度 $O(n \log n)$。

P6944/LOJ3405 [ICPC2018 WF]Gem Island

洛谷这么有实力的吗

考虑最后每个人拿（增加）的绿宝石数量 $a_i$，其概率为：

$$\dbinom{d}{a_1,a_2,\cdots,a_n}\dfrac{a_1!a_2!\cdots a_n!}{n(n+1)\cdots(d+n-1)}=\dfrac{1}{\dbinom{d+n-1}{n-1}}$$

所以只需要对 $\{a\}$ 统计即可。

考虑一个不知道怎么想到的套路的 DP。设 $f_{i,j}$ 表示将 $i$ 有序拆分成 $j$ 个非负整数的方案数，$g_{i,j}$ 表示将 $i$ 有序拆分成 $j$ 个非负整数的前 $r$ 大和。

枚举有 $k$ 个数为正整数，并将它们减去 $1$。于是有：

$$f_{i,j}=\sum\limits_k \dbinom{j}{k} f_{i-k,k}=\dbinom{i+j-1}{i-1}$$

$$g_{i,j}=\sum\limits_k \dbinom{j}{k}(g_{i-k,k}+\min\{r,k\}f_{i-k,k})$$

时间复杂度 $O(nd^2)$。

---

我们发现根本就不想这么 DP，这种问题应该考虑容斥。

设 $f_{i,j}$ 表示恰好有 $i$ 个数大于等于 $j$，则答案即为 $\sum\limits_{i,j} \min\{i,r\} f_{i,j}$。

设 $g_{i,j}$ 表示钦定有 $i$ 个数大于等于 $j$，则 $g_{i,j}=\dbinom{n}{i}\dbinom{d-ij+n-1}{n-1}$。

$$g_{k,j}=\sum\limits_{i \geq k} \dbinom{i}{k} f_{i,j}$$

$$f_{k,j}=\sum\limits_{i \geq k} (-1)^{i-k} \dbinom{i}{k} g_{i,j}=\sum\limits_{i \geq k} (-1)^{i-k} \dbinom{i}{k} \dbinom{n}{i}\dbinom{d-ij+n-1}{n-1}$$

这里有 $jk \leq d$，$ij \leq d$，可以枚举 $j$ 并 $O(\sum\limits_{i} \dfrac{d^2}{i^2})=O(d^2)$ 计算。

---

我不满意！还可以进行一些优化。

$$ANS=\sum\limits_k \min\{k,r\} \sum\limits_{i} (-1)^{i-k} \dbinom{i}{k} \dbinom{n}{i} \sum\limits_j \dbinom{d+n-ij-1}{n-1}$$

改为枚举 $i$：

$$ANS=\sum\limits_{i} \dbinom{n}{i} \Big[\sum\limits_j \dbinom{d+n-ij-1}{n-1}\Big] \Big[\sum\limits_k (-1)^{i-k} \min\{k,r\} \dbinom{i}{k}\Big]$$

后面两部分分开预处理。

前面部分可以用狄利克雷后缀差分，时间复杂度 $O(n \log\log n)$。

后面部分：

$$\sum\limits_{k=1}^d \min\{k,r\} (-1)^k \dbinom{i}{k}=\sum\limits_{k=1}^{\min\{d,r\}} k (-1)^k \dbinom{i}{k}+r\sum\limits_{k=r+1}^d (-1)^k \dbinom{i}{k}$$

设 $t=\min\{d,r\}$，实际上是要算：

$$f_i=\sum\limits_{k=1}^t (-1)^k \dbinom{i}{k}=(-1)^t \dbinom{i-1}{t}-1$$

$$g_i=\sum\limits_{k=1}^t k(-1)^k \dbinom{i}{k}=-i\Big[f_{i-1}+1-(-1)^t \dbinom{i-1}{t}\Big]$$

$$h_i=\sum\limits_{k=1}^d (-1)^k \dbinom{i}{k}$$

可以和答案一起算，时间复杂度 $O(n)$。

总时间复杂度 $O(n \log \log n)$。

CF1630E Expected Components (2900)

最大的问题是如何去重，直接用带权 Burnside 引理：

$$\sum\limits_x \dfrac{w_x}{|\overline x|}=\dfrac{1}{|G|} \sum\limits_g w_(X_g)$$

设有 $d$ 循环节的权值之和为 $f_d$，则答案为 $\dfrac{1}{n} \sum\limits_{d} f_d \varphi(\dfrac{n}{d})$。

以 $f_n$ 为例，由于要算的是和之和，对每种颜色分开计算。具体而言，将该颜色看作 $1$，其它颜色看作 $0$，最后再乘上其它颜色可重排即可。

枚举 $1$ 恰有 $t$ 段，但若直接插板怎样不重不漏仍然是个问题。

用常见套路，枚举旋转最小角度。注意 $0$ 位置不一定是 $1$，还要算 $0$ 位置是 $0$ 的情况。最后范德蒙德卷积即可做到 $O(1)$。

设共有 $q$ 种颜色，则枚举的 $d$ 数量不超过 $\gcd\{b_i\} \leq \min\{b_i\} \leq \lfloor \dfrac{n}{q} \rfloor$，总时间复杂度是 $O(n)$。

XXI OpenCup Grand Prix of SPb J Justice For Everyone

先考虑没有两个人不能相等的限制怎么做。

设 $d_i=b_i-a_i$，$s=\dfrac{\sum d_i}{2}$。

设 $n$ 元生成函数 $F=\sum\limits_{1 \leq i < j \leq n} x_ix_j=\dfrac{1}{2}[(\sum x_i)^2-(\sum x_i^2)]$，则答案为 $[\prod x_i^{d_i}] F^s$。

大力展开：

$$\begin{aligned} Ans &=[\prod x_i^{d_i}] F^s\\ &=\dfrac{1}{2^s} [\prod x_i^{d_i}] [(\sum x_i)^2-(\sum x_i^2)]^s\\ &=\dfrac{1}{2^s} [\prod x_i^{d_i}] \sum\limits_{j=0}^s \dbinom{s}{j} (-1)^j (\sum x_i^2)^j (\sum x_i)^{2s-2j}\\ &=\dfrac{1}{2^s} \sum\limits_{\{e_i\}} \dbinom{s}{\sum e_i} (-1)^{\sum e_i} \dbinom{\sum e_i}{e_1,e_2,\cdots,e_n} \dbinom{\sum d_i-2\sum e_i}{d_1-2e_1,d_2-2e_2,\cdots,d_n-2e_n}\\ \end{aligned}$$

枚举 $\{e_i\}$ 显然不现实，还是用生成函数做。对 $d$ 设 $G_d=\sum\limits_{i=0}^{\lfloor d/2 \rfloor} \dfrac{1}{i! (d-2i)!}$，则答案为：

$$Ans=\dfrac{1}{2^s} \sum\limits_{t=0}^s \dbinom{s}{t} (-1)^{t} t! (2s-2t)!$$

回到原问题，该限制十分类似 LGV 引理的使用条件。将 $G_{b_j-a_i}$ 填入矩阵，计算行列式即可得到答案。

多项式项数为 $O(V^2)=20000$ 较大，可以代值算行列式再多项式快速插值，总时间复杂度 $O(n^3V^2+V^2 \log^2 V)$。

PTZ Camp2022 C3 Inversions

对每个 $t$ 暴力统计逆序对为 $t$ 的排列数量。设 $F_t(x)=\sum\limits_{i=0}^{t-1} x^i$，$G(x)=\prod\limits_{t=1}^n F_t(x)$，答案即为 $\sum\limits_{x=0}^{n(n-1)/2} i^k g_i$。

需要做 $n$ 次值域为 $n^2$ 和 $n$ 的卷积，时间复杂度 $O(n^3)$。

下面假设计算期望。

如果 $k=1$，就是个人人都会的经典问题：每对位置有 $\dfrac{1}{2}$ 的概率产生一个逆序对，因此期望为 $\dfrac{n(n-1)}{4}$。

因此原问题相当于选出 $k$ 对位置，要求每对位置都是逆序对，显然可以分情况讨论得到对应概率。这些位置至多覆盖 $2k$ 个点，故答案一定为关于 $n$ 的 $2k$ 次多项式。然而由于点可以重复，情况数太多，无法直接计算。

同暴力算出 $n=1 \sim 2k$ 时的答案，直接插值，时间复杂度 $O(k^3)$，仍然无法接受。

考虑把 $k$ 次幂用斯特林数拆成下降幂，要求即 $\sum\limits_i i^{\underline{p}}g_i=G^{(p)}(1)$。

对于每个 $F_t(x)$ 这个东西很好求。$F_t^{(p)}(1)=\sum\limits_{i=p}^t i^{\underline{p}}=\dfrac{(t+1)^{\underline{p}}}{p+1}$。

由莱布尼茨公式，$G$ 的 $p$ 次导可以通过对每个 $F_t$ 写出指数型生成函数 $P_t=\sum\limits_i F_t^{(i)} \dfrac{x^i}{i!}$ 卷积得到。

注意此时只需求 $x^{2k}$ 以内的答案，于是时间复杂度变为 $O(k^3)$。使用 NTT 优化即可做到 $O(k^2 \log k)$。

最后我们算的是期望，还要乘上 $n!$ 得到原来的答案，打个表即可。

PTZ Camp2022 H7 Hundred Thousand Points

随机变量不能当离散变量考虑。

首先由于 $\sum a_i >360$ 一定无解，所以 $N$ 是 $O(M)$ 的。

容易发现 $2 \sim n-1$ 的角一定被完全包含在上半平面或下半平面，可以对 $1$ 及 $n$ 的情况分类讨论，然后背包处理。

考虑如何分配空位计算答案，设上半平面的角共有 $num1$ 个，和为 $val1$；下半平面的角共有 $num2$ 个，和为 $val2$，则分配空位的概率为：

$$\dfrac{(180-val1)^{num1}(180-val2)^{num2}}{num1!num2!}$$

（即先将角紧密排成一排，再在空位中插入 $num$ 个断点分配给每个空隙）

• $1$ 及 $n$ 同样不跨越水平线。此时所有变量都可以一视同仁，直接 DP 记录 $num$ 与 $val$ （本质是卷积）再计算答案即可。

• $1$ 跨越水平线，而 $n$ 不跨越水平线。先对 $2 \sim n$ DP，设 $1$ 在上半平面的角度为 $x$，则答案即为：

$$\dfrac{1}{num1!num2!} \int_{0}^{a_i} (180-val1-x)^{num1} (180-val2-a_1+x)^{num2} dx$$

$n$ 跨越水平线，$1$ 不跨越水平线的情况翻转同理。

• $1$ 及 $2$ 均跨越水平线。类似答案为：

$$\dfrac{1}{num1!num2!} \int_{0}^{a_1} \int_{0}^{a_n} (180-val1-x-y)^{num1} (180-val2-a_1-a_n+x+y)^{num2} dx dy$$

改为对 $z=x+y$ 积分。不妨设 $a_1 \leq a_n$，则 $z$ 的贡献系数长这样：

综上，设 $M=180$，卷积部分 $O(M^3)$，积分统计答案 $O(M^4)$（听说可以 NTT 优化到 $O(M^3 \log M)$）。

细节：积分时需要注意变量的上下界。

CF773E Special Positions (3300)

先把期望拆开，对每个位置算贡献。考虑第 $i$ 个位置，设 $m$ 个关键点到它的距离排序后为 $d_1,\cdots,d_m$，则贡献为 $\sum\limits_{i=1}^m \dfrac{d_i}{2^i}$。

然而由于 $i$ 左右都有关键点，不方便排序，难以处理。

考虑不排序，直接计算 $j$ 到 $i$ 的贡献。设 $p_t$ 表示 $t$ 是否为关键点，$cnt_t=\sum\limits_{i=0}^t p_i$，$pre_t=2^{cnt_t}$。

先考虑 $j<i$ 的情况，贡献为 $\sum\limits_{j<i} p_j(i-j) \dfrac{pre_{j-1}}{pre_{2i-j}}=i\sum\limits_{j<i} p_j \dfrac{pre_{j-1}}{pre_{2i-j}}-\sum\limits_{j<i} jp_j \dfrac{pre_{j-1}}{pre_{2i-j}}$，两边分别做。

如果没有 $j<i$ 的限制就能直接卷积了。用 CDQ 分治（好像就是分治NTT），每次让左区间的点做 NTT 贡献右边即可。

$j>i$ 的情况翻过来同理，注意 $j$ 与 $2i-j$ 都是关键点时会算重，改为计算 $\sum\limits_{j<i} p_j(i-j) \dfrac{pre_{j-1}}{pre_{2i-j-1}}$ 即可。

时间复杂度 $O(n \log^2 n)$。

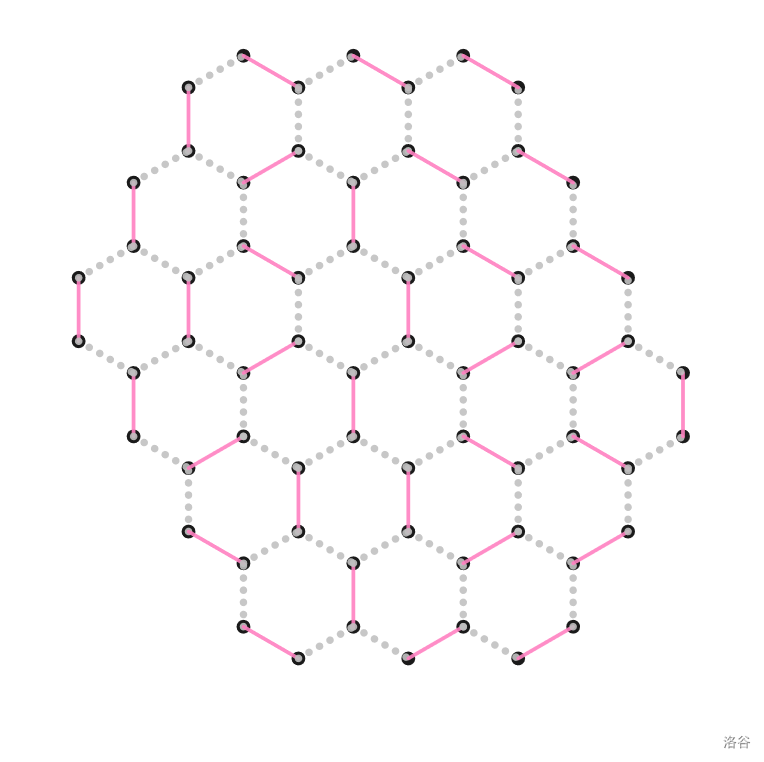
P8114 [Cnoi2021]六边形战士

Part 1

二分图完美匹配看起来难以处理……

一个奇特的想法：将所有灰边（非匹配边）割开，将每条匹配边分离开来，画一画：

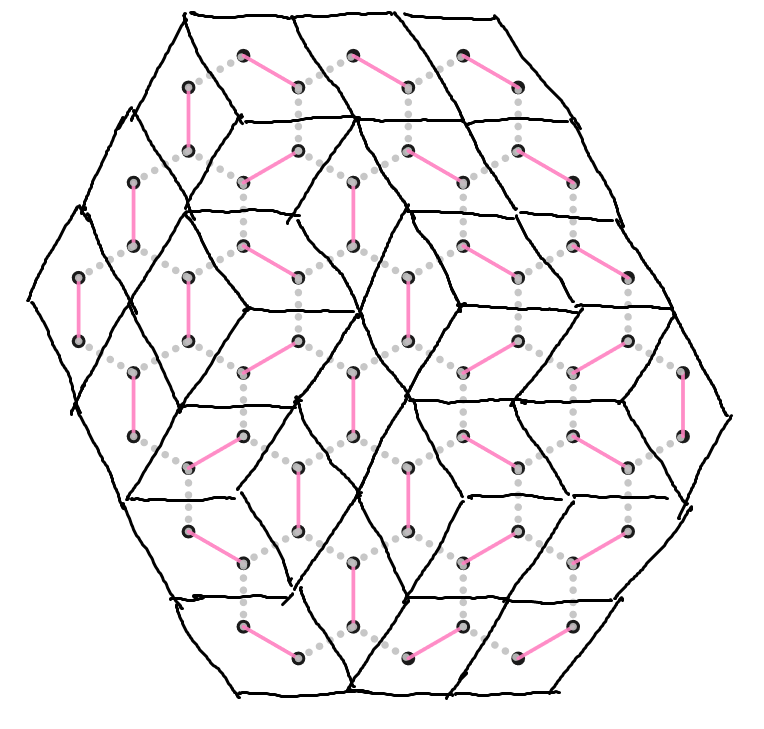
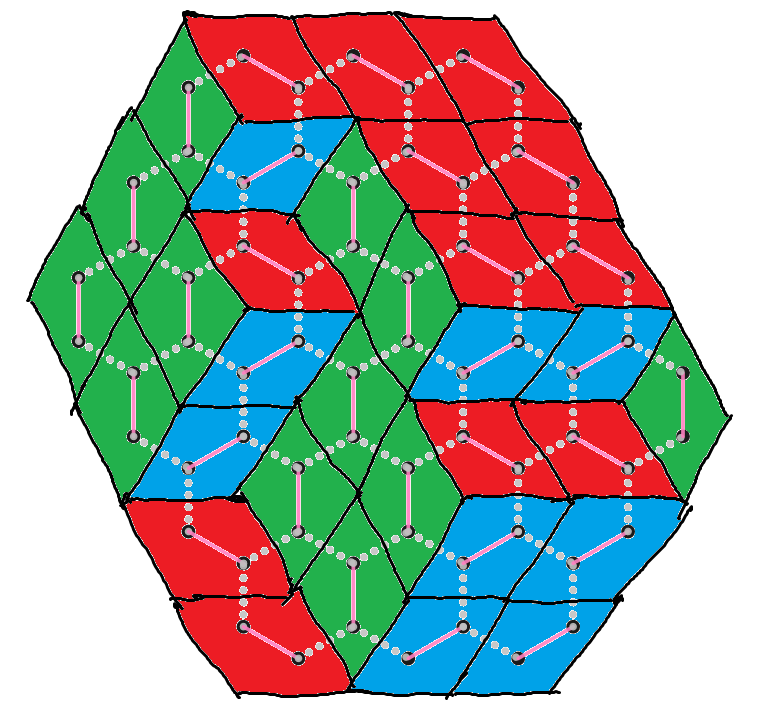
十分的有立体感？不妨再把三种方向的菱形染成不同颜色：

事实上，原图的一种二分图完美匹配对应一种 $a \times b \times c$ 的立方形堆叠。证明见此。

现在题目变成了立方体堆叠计数。这是经典问题，画出 $1 \sim c$ 的轮廓线，限制仅是轮廓线不能互相穿过：

将第 $i$ 条线的起点和终点都向右上平移 $i$ 格，这样就变成了轮廓线不能相交。

考虑 LGV 引理，第 $i$ 个起点到第 $j$ 个终点的方案数为 $\dbinom{a+b}{a+i-j}$。因此答案为：

$$ANS=\det \Big(\dbinom{a+b}{a+i-j} \Big)_{i,j}$$

---

Part 2

把每一行拎出来提系数。第 $i$ 行为 $\dbinom{a+b}{a+i-1},\dbinom{a+b}{a+i-2},\cdots,\dbinom{a+b}{a+i-c}$，提出 $\dfrac{(a+b)!}{(a+i-1)!(b+c-1)!}$ 就得到 $\dfrac{(a+i-1)!}{(a+i-j)!} \dfrac{(b+c-i)!}{(b+j-j)!}=\prod\limits_{k=1}^{j-1} (a+i-k) \prod\limits_{k=j}^c (b+k-i)$。

$$\begin{aligned} ANS &=\Big(\prod\limits_{i=1}^c \dfrac{(a+b)!}{(a+i-1)!(b+c-i)!}\Big) \det \Big(\prod\limits_{k=1}^{j-1} (a+i-k) \prod\limits_{k=j}^c (b+k-i) \Big)_{i,j}\\ &=\prod\limits_{i=1}^c (-1)^{c-i} \Big(\prod\limits_{i=1}^c \dfrac{(a+b)!}{(a+i-1)!(b+c-i)!}\Big) \det \Big(\prod\limits_{k=2}^{j} (a+i-k+1) \prod\limits_{k=j}^c (i-b-k) \Big)_{i,j} \end{aligned}$$

套用题目给出的 Krattenthaler’s formula：

$$\det \Big(\prod\limits_{k=2}^{j} (x_i+a_k) \prod\limits_{k=j+1}^n (x_i+b_k) \Big)_{i,j}=\prod\limits_{1 \leq i<j \leq n} (x_i-x_j) \prod\limits_{2 \leq i \leq j \leq n} (a_i-b_j)$$

$$ANS=(-1)^{c(c-1)/2} \Big(\prod\limits_{i=1}^c \dfrac{(a+b)!}{(a+i-1)!(b+c-i)!}\Big) \prod\limits_{1 \leq i<j \leq c} (i-j) \prod\limits_{2 \leq i \leq j \leq c} (a-i+b+j+1)$$

枚举 $i-j$：

$$\begin{aligned} \prod\limits_{1 \leq i<j \leq c} (i-j)&=(-1)^{c(c-1)/2} \prod\limits_{1 \leq i<j \leq n} (j-i)\\ &=(-1)^{c(c-1)/2} \prod\limits_{t=1}^{c-1} t^{c-t}\\ &=(-1)^{c(c-1)/2} \prod\limits_{t=1}^{c-1} t!\\ \end{aligned}$$

$$\begin{aligned} \prod\limits_{2 \leq i \leq j \leq c} (a-i+b+j+1)&=\prod\limits_{t=0}^{c-2} (a+b+1+t)^{c-1-t}\\ &=\prod\limits_{t=1}^{c-1} (a+b+t)^{c-t}\\ &=\prod\limits_{t=1}^{c-1} (a+b+t)^{\underline{t}}\\ \end{aligned}$$

到这里已经可以 $O(n)$ 计算了。

我不满意！

$$\begin{aligned} ANS&=\Big(\prod\limits_{i=1}^c \dfrac{(a+b)!}{(a+i-1)!(b+c-i)!}\Big) \prod\limits_{t=1}^{c-1} t! \prod\limits_{t=1}^{c-1} (a+b+t)^{\underline{t}}\\ &=\prod\limits_{i=1}^c \dfrac{1}{(a+i-1)!(b+c-i)!} \prod\limits_{t=1}^{c-1} t! \prod\limits_{t=1}^{c-1} (a+b+t)!\\ \end{aligned}$$

记 $H(n)=\prod\limits_{i=0}^{n-1} i!$，就有：

$$ANS=\dfrac{H(a)H(b)H(c)}{H(a+b)H(b+c)H(c+a)H(a+b+c)}$$

总时间复杂度 $O(n)$。

LOJ6215「美团 CodeM 决赛」bt

首先不得不考虑 $u=v$ 的情况，即为二叉树叶子个数之和。简单推一推可得 $\dbinom{2(n-1)}{n-1}$。

$k$ 次幂难做，套路拆成下降幂及组合数：

$$l^k=\sum\limits_{i=0}^k i! S2(k,i) \dbinom{l}{i}$$

转而数其组合意义。相当于在 $u$ 到 $v$ 的路径上特殊标记了 $k$ 个点，再数方案数。

考虑大力设出生成函数，多加一维 $y$ 表示标记个数。设 $F_0,F_1,F_2$ 分别表示子树内包含 $u,v$ 中 $0,1,2$ 个点的生成函数（为了方便，这里不计算 $u,v,lca$ 的贡献，最后乘上 $x^3(1+y)^3$ 即可）。有：

$$F_0=1+xF_0^2$$

$$F_1=1+2x(y+1)F_0F_1$$

$$F_2=F_1^2+2xF_0F_2$$

大力解得：

$$F_0=\dfrac{1-\sqrt{1-4x}}{2x}$$

$$F_1=\dfrac{-1}{y-(y+1)\sqrt{1-4x}}$$

$$F_2=\dfrac{1}{\sqrt{1-4x}(y-(y+1)\sqrt{1-4x})^2}$$

令 $t=\sqrt{1-4x}$，则 $F_2=t^{-3}[1-(t^{-1}-1)y]^{-2}$。

先将 $F_2$ 暴力展开成关于 $y$ 与 $t^{-1}$ 的二元多项式，再考虑 $[x^n]t^{-k}=[x^n](1-4x)^{-k/2}=[x^n] \sum\limits_i \dbinom{-k/2}{i} (-4)^i=\dbinom{-k/2}{n} (-4)^n$。

至于一半组合数，暴力展开或者参考 $x^{\underline k} (x-1/2)^{\underline k}=\dfrac{(2x)^{\underline {2k}} }{2^{2x}}$，同样 $O(1)$ 计算。

总时间复杂度 $O(n+m^2)$。

LOJ3626「2021 集训队互测」愚蠢的在线法官

显然若有重复的 $A_i$，则有两列完全相同，行列式为 $0$。

否则，由于交换 $A_i$ 及 $A_j$ 对行列式无影响，我们不关心 $\{A_i\}$ 的顺序。为了方便，假设 $A_i$ 是按 dfs 序排列的。

树的结构十分适合递归，考虑递归划分矩阵。

下面记两个子树对应的子矩阵中元素分别记为 $A$，$B$，减去 $w_u$ 后的元素分别记为 $A'$，$B'$。

若 $u$ 在 $A$ 中出现了，则矩阵大概长成这样：

$$\left [ \begin{matrix} w_u & w_u & \cdots & w_u & w_u & \cdots & w_u\\ w_u & A & \cdots & A & w_u & \cdots & w_u\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ w_u & A & \cdots & A & w_u & \cdots & w_u\\ w_u & w_u & \cdots & w_u & B & \cdots & B\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ w_u & w_u & \cdots & w_u & B & \cdots & B\\ \end{matrix} \right ]$$

用第一行消元，变为：

$$\left [ \begin{matrix} w_u & w_u & \cdots & w_u & w_u & \cdots & w_u\\ 0 & A' & \cdots & A' & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ 0 & A' & \cdots & A' & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 & B' & \cdots & B'\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 0 & B' & \cdots & B'\\ \end{matrix} \right ]$$

注意到该矩阵的行列式即为 $w_u$ 乘上 $\{1\}$ 的主子行列式。

若 $u$ 没有出现，手动将矩阵内每个元素减去 $w_u$ 可以得到相同的形式。

问题变为如何快速计算某矩阵 $M$ 内每个元素同时加上 $x$ 后的行列式。有结论：设其为关于 $x$ 的函数 $f(x)$，则 $f(x)=ax+b$。其中 $b=\det(M)$，$a$ 为 $M$ 的所有代数余子式之和。

详细推导如下：

$$\begin{aligned} \det(M') &= \sum\limits_{P} (-1)^{\sigma(P)} \prod\limits_i (M_{i,P_i}+x)\\ &=\sum\limits_{S \subseteq [n]} x^{|S|} \sum\limits_{P} (-1)^{\sigma(P)} \prod\limits_{i \notin S} M_{i,P_i}\\ \end{aligned}$$

当 $|S| \geq 2$ 时，交换 $P$ 中不在 $S$ 中的两个元素，贡献会抵消。只考虑 $|S|=0 / 1$ 的情况。

$$\det(M')=det(M)+x\sum\limits_{t=1}^n \sum\limits_{P} (-1)^{\sigma(P)} \prod\limits_{i \neq t} M_{i,P_i}$$

后面的系数即为 $M$ 的所有代数余子式之和。

因此 DP 记录 $f_u=a$ 及 $g_u=b$。具体过程为：设递归到该层时所有元素已减去 $del$，先将子矩阵中的元素减去 $w_u-del$ 递归得到 DP 值，再合并，最后加回减去的 $w_u-del$。

转移时行列式直接相乘。考虑代数余子式，若选在两个子矩形以外的位置，则贡献为 $0$。否则为其中一个子矩阵的行列式乘上另一个子矩阵的代数余子式。

即 $g_u \leftarrow f_ug_v+f_vg_u$，$f_u \leftarrow f_uf_v$。

总时间复杂度 $O(n)$。叶节点需要特判，有些细节。

LOJ3395「2020-2021 集训队作业」Yet Another Permutation Problem

与 ARC134F 也太像了吧

考虑如何判断一个排列能否在 $k$ 次操作内得到。显然充要条件为 存在连续 $n-k$ 个单调递增的数。

容斥，计算所有极长单调递增连续段长度都小于 $p=n-k-1$ 的排列个数。

后面的限制是简单的，可以直接对段长设生成函数 $F=\sum\limits_{i=0}^p x^i=\dfrac{1-x^{p+1}}{1-x}$ 并卷积；然而极长连续段的限制难以处理（直接卷会算重）。

使用同 ARC134F Flipping Coins 的方法，给每个长度赋一个新的权组成生成函数 $A$，并使 $A$ 任意组合后正好为 $F$：

$$\dfrac{1}{1-A}=F$$

$$A=1-\dfrac{1}{F}$$

于是答案就是 $n![x^n] \dfrac{1}{1-\hat A}$。暴力实现 $O(n^3)$。

注意到 $\dfrac{1}{F}=\dfrac{1-x}{1-x^{p+1}}=\sum\limits_d (1-x)x^{d(p+1)}$ 只有 $O(\lfloor \dfrac{n}{p} \rfloor)$ 项，因而对 $F$ 求逆的复杂度为 $O(n \lfloor \dfrac{n}{p} \rfloor)$。可以接受。

总时间复杂度 $O(n^2 \ln n)$。

2021ICPC 上海站 (GYM103446) B Strange Permutations

将 $i$ 向 $P_i$ 连边，合法的 $Q$ 即不存在相邻的两个数 $Q_i$ 与 $Q_{i+1}$ 相连。

大力对边容斥，若钦定了 $k$ 条边必须在 $Q$ 中相邻，则对应方案数为 $(n-k)!$（每一条边相当于把两个位置合并）。

接下来只需要对每个 $k$ 算出钦定 $k$ 条边的方案数。对每个环，设其长为 $l$，则写出生成函数 $F=(1+x)^l-x^l$，将所有 $F$ 卷起来即可得到答案。

使用分治乘，时间复杂度 $O(n \log^2 n)$。

2021CCPC 广州站 (GYM103415) K Magus Night

意识到 $\text{lcm} \geq p$ 十分的怪异（因为 $\text{lcm}$ 可以非常大） ，于是考虑容斥，计算 $\gcd \leq q$ 的方案减去 $\gcd \leq q \wedge \text{lcm} < p$ 的方案。

第一个问题非常好算。设 $f_d$ 表示 $\gcd =d$ 的方案，$g_d$ 表示钦定每个数都被 $d$ 整除的方案。则：

$$g_d=\sum\limits_{i \mid d} f_i$$

可以莫比乌斯反演得到 $f_d=\sum\limits_{i \mid d} \mu(\dfrac{d}{i}) g_i$。

第二个问题用同样的方法，现在需要对每个 $d$ 求出每个数都被 $d$ 整除且 $\text{lcm} < p$ 的方案，即任意选数 $\text{lcm} \leq \lfloor \dfrac{p-1}{d} \rfloor$ 的方案。

再套容斥，设 $p_d$ 表示 $\text{lcm}=d$ 的方案，$q_d$ 为钦定每个数都整除 $d$ 的方案（可以通过算约数和处理）。则：

$$q_d=\sum\limits_{d \mid i} p_i$$

可以用倍数莫比乌斯反演得到 $p_d=\sum\limits_{d \mid i} \mu(\dfrac{i}{d}) q_i$。

总时间复杂度 $O(m (\ln m+\log n))$。

LOJ3393「2020-2021 集训队作业」Game on Tree

记 $u$ 子树内叶子节点集合为 $L_u$，到 $1$ 号点深度为偶数的非叶节点集合为 $A_u$，深度为奇数的非叶节点集合为 $B_u$。

考虑 DP。设 $f_{u,i,j}$ 表示 $u$ 的子树合法，Alice 的最优值为 $i$ 且 Bob 的最优值为 $j$ 的方案数。$x_{u,i}$ 表示 $u$ 的子树中 Alice 的最优值不超过 $i$ 的方案数；$y_{u,i}$ 表示 $u$ 的子树中 Bob 的最优值不超过 $i$ 的方案数。

考虑转移，不妨设 $u \in A$，$l$ 与 $r$ 分别表示左右儿子，考虑 Alice 选择接在哪边，则有：

$$f_{u,i,j}=f_{l,i,j}x_{r,i}+f_{r,i,j}x_{l,i}$$

$$x_{u,i}=2x_{l,i}x_{r,i}$$

$$y_{u,i}=2^{|A_r|+|B_r|}k^{2|L_r|}y_{l,i}+2^{|A_l|+|B_l|}k^{2|L_l|}y_{r,i}$$

注意到 $x$ 与 $y$ 似乎关联性不大。考虑做一些变换使 $x$ 与 $y$ 独立。

朴素的想法是令 $x'_{u,i}=x_{u,i}/(2^{|A_u|+|B_u|}k^{2|L_u|}i)$，$y'_{u,i}=y_{u,i}/(2^{|A_u|+|B_u|}k^{2|L_u|}i)$，然而带入第三个式子后会出现 $/2$（因为 $A_u=A_l+A_r+1$），模数不为质数难以处理。

将 $A$ 和 $B$ 分开在 $x$ 与 $y$。令 $x'_{u,i}=x_{u,i}/(2^{|A_u|}k^{|L_u|}i)$，$y'_{u,i}=y_{u,i}/(2^{|B_u|}k^{|L_u|}i)$，则递推式变为：

$$f_{u,i,j}=2^{|A_r|}k^{2|L_r|}f_{l,i,j}x'_{r,i}+2^{|A_l|}k^{2|L_l|}f_{r,i,j}x'_{l,i}$$

$$x'_{u,i}=ix'_{l,i}x'_{r,i}$$

$$y'_{u,i}=2^{|A_r|}k^{|L_r|}y'_{l,i}+2^{|A_l|}k^{|L_l|}y'_{r,i}$$

这时发现 $f_{u,i,j}=x_{u,i}y_{u,j}$，边界条件为 $x_{leaf,i}=y_{leaf,i}=1$，答案即为 $(\sum x_{u,i})(\sum y_{u,i})$。

视多项式 $F_u(x)$ 满足 $F_u(i)=x_{u,i}$。由于上述转移过程中每次只会使多项式系数 $+1$，所有节点系数的多项式至多为 $n-1$。可以 $O(n^2)$ 处理 $0 \sim n$ 的点值，再用拉格朗日插值得到答案。

具体而言，考虑拉格朗日插值公式：

$$F(x)=\sum\limits_{i=0}^n y_i \prod\limits_{j \neq i} \dfrac{x-x_j}{x_i-x_j}$$

预处理出 $l_i(k)=\prod\limits_{j \neq i} \dfrac{k-x_j}{x_i-x_j}$，每个询问带入求值即可。然而模数不是质数，无法取逆。

注意到拉格朗日基本多项式 $l_i(x)$ 在 $i$ 处为 $1$，在 $[0,n] \setminus \{i\}$ 处为 $0$，故其为整值多项式，一定可以表示为 $\sum\limits_{t=0}^n c_t \dbinom{x}{t} (c_t \in \Z)$ 的形式。

有：

$$y_p=\sum\limits_{t=0}^p c_t \dbinom{p}{t}=[p=i]$$

$$c_p=\sum\limits_{t=0}^p (-1)^{p-t} y_t \dbinom{p}{t}=(-1)^{p-i} \dbinom{p}{i}$$

$$l_i(k)=\sum\limits_{t=i}^n (-1)^{t-i} \dbinom{t}{i} \dbinom{k}{t}$$

只要处理出 $\dbinom{k}{t}$ 即可。

不断将组合数乘上 $k-i+1$，再除掉 $i$，运算过程不会出现分数。故将一个数分成两部分：其含 $p$ 的质因数的指数 及 与 $p$ 互质的部分，即可通过欧拉定理求逆。

时间复杂度 $O(n^2)$。

LOJ3630「2021 集训队互测」Imbalance

记前缀和为 $\{s_i\}$。考虑 $\{s_i-s_{i-k}\}$，其为连续变化的（即差值在 $[-1,1]$ 间），故要么所有 $s_i-s_{i-k}<\dfrac{k}{2}$，要么所有 $s_i-s_{i-k}>\dfrac{k}{2}$。不妨考虑第一种情况，第二种情况反转同理。

将所有第 $i$ 个点画到第 $i \bmod k$ 个位置上，会形成 $\lfloor \dfrac{n}{k} \rfloor$ 条折线。再将第 $t$ 条折线向下平移 $t \cdot \dfrac{k}{2}$（即对应 $(i \bmod k,s_i-\lfloor \dfrac{i}{k} \rfloor \dfrac{k}{2})$），则原条件转化为 $\lfloor \dfrac{n}{k} \rfloor$ 条折线两两不交。

...

CF1654H Three Minimums (3500)

标记记号 $check[i,<]=[i>m \vee s_i='<']$，$check[i,<]=[i>m \vee s_i='>']$。

考虑一个序列是否是好的：

• 若 $1$ 不在两端，设 $p_i=1$，则 $p[1:n]$ 合法当且仅当 $p[1:i]$ 与 $p[i:n]$ 合法；

• 若 $1$ 在两端（不妨设 $p_1=1$）：

  • 若 $2$ 不在另一端，设 $p_j=2$，则 $p[1:n]$ 合法当且仅当 $p[1:j]$ 与 $p[j:n]$ 合法。

  • 否则 $p_n=2$，则 $p[1:n]$ 合法当且仅当 「$p_2=3$，$p[2:n]$ 是好的」 或者 「$p_{n-1}=3$，$p[1:n-1]$ 是好的」。

于是设计一个区间 DP。设 $a_{**}(l,r),a_{1*}(l,r),a_{*1}(l,r),a_{12}(l,r),a_{21}(l,r)$ 分别表示对于区间 $(l,r)$，满足给定条件的「区间两端无限制」，「区间左端点为最小值」，「区间右端点为最小值」，「区间左端点为最小值，右端点为次小值」，「区间左端点为次小值，右端点为最小值」的方案数。于是有：

$$a_{**}(l,r)=\sum\limits_{i=l}^r a_{*1}(l,i) a_{1*}(i,r) \dbinom{r-l}{i-l}$$

$$a_{1*}(t,t)=1,a_{1*}(l,r)=\sum\limits_{i=l+1}^r a_{12}(l,i) a_{1*}(i,r) \dbinom{r-l-1}{i-l-1}$$

$$a_{*1}(t,t)=1,a_{*1}(l,r)=\sum\limits_{i=l}^{r-1} a_{*1}(l,i) a_{21}(i,r) \dbinom{r-l-1}{i-l}$$

$$a_{12}(t,t+1)=check[t,<],a_{12}(t,t+2)=check[t,<]check[t+1,>],a_{12}(l,r)=check[l,<]a_{21}(l+1,r)+check[r-1,>]a_{12}(l,r-1)$$

$$a_{21}(t,t+1)=check[t,>],a_{21}(t,t+2)=check[t,<]check[t+1,>],a_{21}(l,r)=check[l,<]a_{21}(l+1,r)+check[r-1,>]a_{12}(l,r-1)$$

暴力做时间复杂度 $O(n^3)$，无法接受。

---

答案为 $a_{**}(1,n)$，故要对所有 $k \in [k,n]$ 计算出 $a_{*1}(1,k)$ 及 $a_{1*}(k,n)$。

Part 1：$a_{*1}(1,k)$

DP 式为 $a_{*1}(1,1)=1$，$a_{*1}(1,k)=\sum\limits_{i=1}^{k-1} a_{*1}(1,i) a_{21}(i,k) \dbinom{k-2}{i-1}$。

观察到给左右两边的 $a_{*1}$ 同乘阶乘会使形式简化许多。设 $a_{*1}(1,k)=(k-1)!x_{k-1},x_0=1$，则有：

$$(k-1)!x_{k-1}=\sum\limits_{i=1}^{k-1} (i-1)!x_{i-1} a_{21}(i,k) \dfrac{(k-2)!}{(i-1)!(k-i-1)!}$$

$$(k-1)x_{k-1}=\sum\limits_{i=1}^{k-1} x_{i-1} a_{21}(i,k) \dfrac{1}{(k-i-1)!}$$

$$k x_k=\sum\limits_{i=1}^k x_{i-1} a_{21}(i,k+1) \dfrac{1}{(k-i)!}$$

$$k x_k=\sum\limits_{i=0}^{k-1} x_i \dfrac{a_{21}(i+1,k+1)}{(k-i-1)!}$$

这个形式很好看，但是 $a_{21}(i+1,k+1)$ 有两个变量而难以处理。

注意到限制只在前 $m$ 位处，故对于 $l>m$ 的状态，其 DP 值只与长度 $r-l+1$ 有关。设 $b_{??}(k)=a_{??}(m+1,m+k)$。上式就可以改写为：

$$k x_k=\sum\limits_{i=0}^{k-1} x_i \dfrac{b_{21}(k-i+1)}{(k-i-1)!}+\sum\limits_{i=0}^{\min(k-1,m-1)} x_i \dfrac{a_{21}(i+1,k+1)-b_{21}(k-i+1)}{(k-i-1)!}$$

记 $u_i=\dfrac{b_{21}(i+2)}{i!}$，$v_{k-1}=\sum\limits_{i=0}^{\min(k-1,m-1)} x_i \dfrac{a_{21}(i+1,k+1)-b_{21}(k-i+1)}{(k-i-1)!}$。则：

$$k x_k=v_{k-1}+\sum\limits_{i=0}^{k-1} x_i u_{k-i-1}$$

写成生成函数就是 $X'=V+UX$，解这个微分方程得到 $X=\exp(\int U)\Big[1+\int \Big( V \exp(-\int U) \Big) \Big]$。

注意到 $b_{21}(k)=2^{k-2}+[k=1]$，对所有 $l \in [1,m+1]$，$r \in (l,n]$ 暴力 DP 出 $a_{21}(l,r)$ 即可得到 $b_{21}(k)$，再对所有 $t \in [1,m]$ 暴力 DP 得到 $x_t$，即可计算 $U$ 与 $V$。

Part 2：$a_{1*}(k,n)$

注意到 $k>m$ 时 $a_{1*}(k,n)=b_{1*}(n-k+1)$，考虑先求出 $b_{1*}(k)$，求出后可对 $k \in [1,m]$ 暴力 DP 出 $a_{1*}(k,n)$。

DP 式为 $a_{1*}(n,n)=1,a_{1*}(k,n)=\sum\limits_{i=k+1}^n a_{12}(k,i) a_{1*}(i,n) \dbinom{n-k-1}{i-k-1}$，即：

$$b_{1*}(k)=\sum\limits_{i=2}^{k} b_{12}(i) b_{1*}(k-i+1) \dbinom{k-2}{i-2}=\sum\limits_{i=1}^{k-1} b_{1*}(i) b_{12}(k-i+1) \dbinom{k-2}{i-1}$$

令 $b_{1*}(k)=(k-1)!y_{k-1}$，代入：

$$(k-1)! y_{k-1}=\sum\limits_{i=1}^{k-1} (i-1)! y_{i-1} b_{12}(k-i+1) \dfrac{(k-2)!}{(i-1)!(k-i-1)!}$$

$$(k-1) y_{k-1}=\sum\limits_{i=1}^{k-1} y_{i-1} \dfrac{b_{12}(k-i+1)}{(k-i-1)!}$$

$$k y_k=\sum\limits_{i=1}^{k} y_{i-1} \dfrac{b_{12}(k-i+2)}{(k-i)!}$$

$$k y_k=\sum\limits_{i=0}^{k-1} y_{i} \dfrac{b_{12}(k-i+1)}{(k-i-1)!}=\sum\limits_{i=0}^{k-1} y_{i} u_{k-i-1}$$

于是有 $Y'=UY$，解得 $Y=\exp(\int U)$。

总时间复杂度 $O(n(\log n+m))$。

CF1616H Keep XOR Low (3000)

小于等于不好算，改为小于 $x+1$。首先处理出 $x$ 的最高位，显然不能选两个高位不同的 $a_i$，故将所有 $a_i$ 按高位分类。

对所有 $a_i$ 建出字典树，设 $siz_u$ 表示 $u$ 节点子树内的 $a_i$ 个数。下面设 $u_1=ls(u)$，$u_2=rs(u)$。

考虑递推，设 $f_{u,v}$ 表示 选出 $u$ 子树内一些数（不能不选）并选出 $v$ 子树内一些数（不能不选）组成的合法答案数量，则：

$$f_{u,v}=f_{u_1,v_1}+f_{u_2,v_2},x_{dep_u}=0$$

$$f_{u,v}=f_{u_1,v_2}f_{u_2,v_1}+f_{u_2,v_1}(2^{siz_{u_1}}+2^{siz_{v_2}}-1)+f_{u_1,v_2}(2^{siz_{u_2}}+2^{siz_{u_1}}-1)+(2^{siz_{u_1}}-1)(2^{siz_{v_1}}-1)+(2^{siz_{u_2}}-1)(2^{siz_{v_2}}-1),x_{dep_u}=1$$

容易发现一个 $u$ 对应的 $v$ 是唯一的，故状态数量与节点数量同阶。

时间复杂度 $O(n \log a_i)$。

CF1119H Triple (3200)

鸽了好久没写，已经被问过3遍了

$$[x^S]\prod_{t=1}^n \Big(\sum\limits_{i=1}^k p_i x^{a_{t,i}} \Big)$$

暴力即对每一层做 FWT，再点积起来做 IFWT。

考虑到只有 $k$ 种值，故 IFWT 后也只有 $2^k$ 种值。只要算出每个位置上每种值的层数，就能得到答案。

下面定义一种新变换 $\otimes$，$S$ 到 $T$ 的贡献系数为 $S \otimes T=|S \cap T| \bmod 2$。

设 $f_{mask,S}$ 表示 $S$ 中的元素恰好贡献到 $mask$ 的层数，即：

• $$\forall i \in S,a_{t,i} \otimes mask=1$$

• $$\forall i \notin S,a_{t,i} \otimes mask=0$$

再设 $g_{mask,S}$ 表示满足 $(\oplus_{i \in S} a_{t,i}) \otimes mask=1$ 的层数。容易通过 FWT 得到，该部分复杂度 $O(m2^{m+k})$。

考虑 $g_S$ 会被哪些 $f_T$ 统计到。由 $(\oplus_{i \in S} a_{t,i}) \otimes mask=1$：

$$[(\oplus_{i \in S \cap T} a_{t,i}) \otimes mask] \oplus [(\oplus_{i \in S \setminus T} a_{t,i}) \otimes mask]=1$$

$$(\oplus_{i \in S \cap T} a_{t,i}) \otimes mask=1$$

$$|S \cap T| \bmod 2=1$$

$$S \otimes T=1$$

故对 $F$ 作 $\otimes$ 变换即得到 $G$，对 $G$ 作 $\otimes$ 逆变换即得到 $F$。该部分复杂度 $O(k2^{m+k})$。

容易发现 $\otimes$ 变换与 FWTxor 变换是线性关系，故将 $\otimes$ 变换替换为 FWTxor 变换是等价的。

总时间复杂度 $O(n2^k+(m+k)2^{m+k})$。

PTZ Camp2022 B6 Gachapon | PR#3 抽卡

直接 DP。考虑计算 $t$ 的答案，设 $f_{i,j}$ 表示 $i$ 级合法抽卡抽出的卡等级不超过 $j$ 的概率，$g_{i,j}$ 表示 $i$ 级合法抽卡抽出的卡等级不超过 $j$ 的情况中抽到 $t$ 的期望次数。

转移期望时，由于每个子树相同，可以只计算一个子树的贡献，再乘上 $b_i$。

$$f_{i,j} \leftarrow f_{i-1,j}^{b_i}-f_{i-1,i-1}^{b_i}$$

$$g_{i,j} \leftarrow b_i(g_{i-1,j} f_{i-1,j}^{b_i-1}-g_{i-1,i-1} f_{i-1,i-1}^{b_i-1})$$

答案即为 $g_{n,m}$。

枚举 $t$，时间复杂度 $O(nm^2 \log b)$。

注意到对于不同的 $t$，答案状态是相同的。且计算出 $f$ 后 $g$ 的转移是线性的。直接将 $g_{n,m}$ 设为 $1$，倒推即可。

时间复杂度 $O(nm \log b)$。

技巧：动态规划倒推。将转移视为带权边，则产生一张 DAG。定义路径的权为其中所有边权之积。
设初始状态为 $S$，终止状态为 $T$。将 $S$ 的 DP 值设为 $1$，则 $T$ 的 DP 值可视为 $S$ 到 $T$ 的所有路径权值和。
故将所有边反向，权值不变，将 $T$ 的 DP 值设为 $1$，倒着转移可在 $S$ 处得到原先终止状态的 DP 值。

P7519 [省选联考 2021 A/B 卷] 滚榜

显然对每种最终排列计算其对应的最少过题数量，与 $m$ 比较即可判断是否合法。

设排列为 $p_1,p_2,\cdots,p_n$，定义 $p_0$ 为 $a_i$ 最大的中最靠前的 $i$。设 $b_i$ 表示在合法前提下 $p_i$ 的最少过题数量，则有：

• $b_i=b_{i-1},a_{p_i}>a_{p_{i-1}}$

• $b_i=b_{i-1}+a_{p_{i-1}}-a_{p_i}+[p_{i-1}<p_i],a_{p_i} \leq a_{p_{i-1}}$

注意到 $\{b_i\}$ 单调不降，且每次增量与 $b_{i-1}$ 无关。于是在每次加入 $p_i$ 时直接预先给后面所有的 $b_i$ 加上增量，就不必再记录上一个 $b_i$ 的值。

考虑状压 DP，从前到后填 $\{p_i\}$。设 $f_{S,i,j}$ 表示已经填了 $S$ 里的数，最后一个填的数为 $i$，目前 $b_i$ 的和为 $j$ 的方案数，直接转移即可。

时间复杂度 $O(n^2m2^n)$，空间复杂度 $O(nm2^n)$。

PTZ Summer 2021 Day 1 G Generate the Sequences

理解一下题意立即发现题目等价于：

有一变量 $x=0$，每次可以令 $x \leftarrow x+m-2$（$1$ 种方案），$x \leftarrow x$（$1$ 种方案） 或 $x \leftarrow x-1$（$x$ 种方案）。求操作 $n$ 次方案数。

然而 $x$ 的值难以维护，至少要记录 $1,3$ 操作的次数，只能做到 $O(n^3)$。

注意到 $1,3$ 操作与 $2$ 操作是几乎独立的，可以分开考虑，按 $1,3$ 操作 DP 再统计 $2$ 操作的方案数。

考虑类似 ARC112E Cigar Box，对于每次 $2$ 操作不立刻进行，而是将其操作的时间延后。于是每次只需考虑在之后的操作中选出一些做 $2$ 操作。

设 $f_k$ 表示剩下 $k$ 次操作，已经进行的操作的方案数。考虑下一次是 $1$ 操作还是 $3$ 操作，则：

$$f_{k-1} \leftarrow f_k$$

$$f_{k-i-1} \leftarrow \dbinom{k-1}{i} \dbinom{m-2}{i} f_k$$

时间复杂度 $O(n^2)$，显然可以用分治 FFT 优化至 $O(n \log^2 n)$。

PTZ Summer 2021 Day 1 M Multiple Parentheses

设 $C(x)$ 表示卡特兰数的生成函数，则答案为：

$$[x^m][C(x)-c_k x^k]^n$$

常数很小的多项式快速幂能过吗

拆开（或容斥）后只需快速计算 $S(n,k)=[x^n]C^k(x)$ 即可。

结论：

$$[x^n]C^k(x)=\dbinom{k-1+2n}{n}-\dbinom{k-1+2n}{n-1}=\dfrac{k}{k+n} \dbinom{k-1+2n}{n}$$

组合证明：相当于 $k$ 个合法括号拼起来。尝试建立其与由 $(0,k-1)$ 走到 $(2n+k-1,0)$ 的 $\text{Dyck}$ 路径的双射：

• 括号序列组 $\rightarrow$ 路径：依此按照每个括号序列行走，在走完每个括号序列后额外向右下走一步。
• 路径 $\rightarrow$ 括号序列组：取所有前缀 min 作为断点将整条路径分为 $n$ 条路径，从而对应括号序列组。

时间复杂度 $O(n+m)$。

PTZ Winter 2021 Day 8 G Biological Software Utilities

不会组合做法

考虑如何判断一棵树是否为二分图。可以类似拓扑排序不断删掉叶子，看是否能删空。

具体而言，设 $dp_u$ 表示 $u$ 是否与子树内的匹配。则：

$$dp_u= \begin{cases} 1, 子树内全为 0\\ 0, 子树内恰有一个 1 \end{cases}$$

若子树内有多个 $1$ 则整棵树不合法。

上生成函数。设 $F(x),G(x)$ 分别表示根的 DP 值为 $0,1$ 的有标号有根树的指数型生成函数。则：

$$F(x)=xG(x) \exp F(x)$$

$$G(x)=x\exp F(x)$$

于是 $F(x)=G(x)^2$，代入得：

$$\sqrt{F(x)}=x \exp F(x)$$

$$\ln \dfrac{F(x)}{x^2}=2 F(x)$$

注意 $F(x)$ 只在偶数项有值，令 $F(x)=P(x^2)$，则：

$$\ln \dfrac{P(x^2)}{x^2}=2 P(x^2)$$

$$\ln \dfrac{P(x)}{x}=2 P(x)$$

设 $Q(x)$ 为 $P(x)$ 的复合逆。

$$\ln \dfrac{x}{Q(x)}=2 x$$

$$\dfrac{x}{Q(x)}=e^{2x}$$

由拉格朗日反演：

$$\begin{aligned} [x^n]P(x) &=\dfrac{1}{n} [x^{n-1}] (\dfrac{x}{Q(x)} )^n\\ &= \dfrac{1}{n} [x^{n-1}] e^{2nx}\\ &= \dfrac{(2n)^{n-1}}{n!}\\ \end{aligned}$$

故 $f_n=\dfrac{n^{n/2-1}}{(n/2)!}(2 \mid n)$。

答案即为：

$$Ans= \begin{cases} 0, 2 \nmid n\\ \dfrac{(n-1)! n^{n/2-1}}{(n/2)!}, 2 \mid n \end{cases}$$

总时间复杂度 $O(n)$。

LOJ6495 「雅礼集训 2018 Day1」树

为什么网上全是 n^4 | 为啥不出 n=1000

假装没有第一问，不考虑精度问题。

从上往下 DP，设 $f_{i,j}$ 表示子树大小为 $i$，深度为 $j$ 的方案数。考虑根的最前面的儿子，转移即：

$$f_{i+j,\max(p,q+1)} \leftarrow \dbinom{i+j-2}{i-1} f_{i,p} f_{j,q}$$

枚举 $i+j$ 分层转移，朴素转移 $O(n^4)$。

注意到第二维相当于 $\max$ 卷积，前缀和/差分优化即可做到 $O(n^3)$。

注意到第一维相当于多项式卷积，再上个 NTT 即可做到 $O(n^2 \log n)$。

LOJ3120 [CTS2019] 珍珠

记 $c=\min(d,n-2m)$，相当于要求出现奇数次的颜色不超过 $c$ 种。

$$\begin{aligned} Ans&=[x^n] \sum\limits_{i=0}^c \dbinom{d}{i} (\dfrac{e^x-e^{-x}}{2})^i (\dfrac{e^x+e^{-x}}{2})^{d-i}\\ &=2^{-d} [x^n] e^{-d} \sum\limits_{i=0}^c \dbinom{d}{i} (e^{2x}-1)^i (e^{2x}+1)^{d-i} \end{aligned}$$

记 $F(x)=\sum\limits_{i=0}^c \dbinom{d}{i} (x-1)^i (x+1)^{d-i}$，则 $Ans=2^{-d} \sum\limits_{i=0}^d (2i-d)^n$。下面考虑计算 $F(x)$。

$F(x)$ 是 D-finite 的，考虑对其求导：

$$F'(x)=\sum\limits_{i=0}^c \dbinom{d}{i} i(x-1)^{i-1} (x+1)^{d-i}+\sum\limits_{i=0}^c \dbinom{d}{i} (d-i) (x-1)^{i} (x+1)^{d-i-1}$$

$$\begin{aligned} dF(x)&=\sum\limits_{i=0}^c \dbinom{d}{i} i (x-1)^i (x+1)^{d-i}+\sum\limits_{i=0}^c \dbinom{d}{i} (d-i) (x-1)^i (x+1)^{d-i}\\ &=(x-1) \sum\limits_{i=0}^c \dbinom{d}{i} i (x-1)^{i-1} (x+1)^{d-i}+(x+1)\sum\limits_{i=0}^c \dbinom{d}{i} (d-i) (x-1)^{i} (x+1)^{d-i-1}\\ &=xF'(x)+\sum\limits_{i=0}^c \dbinom{d}{i} (d-i) (x-1)^{i} (x+1)^{d-i-1}-\sum\limits_{i=0}^c \dbinom{d}{i} i (x-1)^{i-1} (x+1)^{d-i}\\ &=xF'(x)+\sum\limits_{i=0}^c \dbinom{d}{i} (x-1)^{i-1} (x+1)^{d-i-1}[(d-i)(x-1)-i(x+1)]\\ &=xF'(x)+\sum\limits_{i=0}^c \dbinom{d}{i} (x-1)^{i-1} (x+1)^{d-i-1}[d(x-1)-2ix]\\ &=xF'(x)+d\sum\limits_{i=0}^c \dbinom{d}{i} (x-1)^i (x+1)^{d-i-1}-2dx \sum\limits_{i=0}^c \dbinom{d-1}{i-1} (x-1)^{i-1} (x+1)^{d-i-1}\\ &=xF'(x)+d \{ \sum\limits_{i=0}^c (x-1)^{i-1} (x+1)^{d-i-1}[(x-1)\dbinom{d}{i}-2x\dbinom{d-1}{i-1}] \} \\ &=xF'(x)+d \{ \sum\limits_{i=0}^c (x-1)^{i-1} (x+1)^{d-i-1}[(x-1)\dbinom{d-1}{i}-(x+1)\dbinom{d-1}{i-1}] \} \\ &=xF'(x)+d \{ \sum\limits_{i=0}^c \dbinom{d-1}{i} (x-1)^{i} (x+1)^{d-i-1} - \sum\limits_{i=0}^c \dbinom{d-1}{i-1} (x-1)^{i-1} (x+1)^{d-i} \} \\ &=xF'(x)+d \{ \sum\limits_{i=0}^c \dbinom{d-1}{i} (x-1)^{i} (x+1)^{d-i-1} - \sum\limits_{i=0}^{c-1} \dbinom{d-1}{i} (x-1)^{i} (x+1)^{d-i-1} \} \\ &=xF'(x)+d \dbinom{d-1}{c} (x-1)^{c} (x+1)^{d-c-1} \\ \end{aligned}$$

即 $(d-\vartheta)F(x)=d \dbinom{d-1}{c} (x-1)^{c} (x+1)^{d-c-1}$。设 $a=c,b=d-c-1$，只需快速计算 $G(x)=(x-1)^{a} (x+1)^{b}$ 即可。

$G(x)$ 也是 D-finite 的，对其求导：

$$G'(x)=a(x-1)^{a-1}(x+1)^b+b(x-1)^a(x+1)^{b-1}=G(x)(\dfrac{a}{x+1}+\dfrac{b}{x-1})$$

$$(x^2-1)G'(x)=[(a+b)x+(a-b)]G(x)$$

$$-(i+1)g_{i+1}=(a-b)g_i+(a+b-i+1)g_{i-1}$$

于是可以线性递推。

计算答案时，求 $i^n$ 可以线性筛，复杂度 $O(\dfrac{d \log n}{\ln d})=O(d \log_d n)$。

总时间复杂度 $O(d \log_d n)$。

LOJ2554「CTSC2018」青蕈领主

显然若将每个 $i$ 对应的区间 $[i-a_i+1,i]$ 画出，这些区间一定形成树的结构，否则不合法。

具体而言，区间 $[i-a_i+1,i-1]$ 一定能被分成若干极长连续的子区间（即儿子）。可以将每个子区间看成一个数，故设子区间个数为 $son_u$，只需要求出形如 1 1 ... 1 n+1 问题的答案 $f_n$，答案即为 $\prod\limits_u f_{son_u}$。

利用递归的结构，设 $G(x)=\sum\limits_{i=1}^{+ \infty} i! x^i$，则有：

$$G(x)=xF(G(x))+x$$

$$F(G(x))+1=\dfrac{G(x)}{x}$$

设 $R(x)$ 为 $G(x)$ 的复合逆，代入 $R(x)$ 可得：

$$F(x)=\dfrac{x}{R(x)}-1$$

接下来只需要求 $R(x)$ 即可。注意到 $G(x)$ 是 D-finite 的，可知 $(x-1)G(x)+x^2 G'(x)+x=0$，代入 $R(x)$ 得：

$$x(R(x)-1)+R(x)^2 G'(R(x))+R(x)=0$$

由 $1=G(R(x))'=R'(x) G'(R(x))$，

$$x(R(x)-1)+\dfrac{R(x)^2}{R'(x)}+R(x)=0$$

$$xR(x)R'(x)-xR'(x)+R(x)^2+R(x)R'(x)=0$$

$$\sum\limits_{i=1}^{n-1} ir_ir_{n-i}+\sum\limits_{i=1}^{n-1} r_ir_{n-i}+\sum\limits_{i=1}^{n} ir_ir_{n+1-i}=nr_n$$

$$-r_n=\sum\limits_{i=1}^{n-1} (i+1)r_ir_{n-i}+\sum\limits_{i=2}^{n-1} ir_ir_{n+1-i}$$

分治 FFT 即可。时间复杂度 $O(n \log^2 n)$。

LOJ3726「SDOI / SXOI2022」多边形

对一条边考虑，关注边上的顶点（不含两端）。由于允许这些点不连边，先枚举哪些点连边。

凸 $n$ 边形的三角剖分有 $Catalan(n-2)$ 种，但如果存在原本在同一条边的两个点连边就会不合法。

考虑容斥。记恰跨过一个（选中的）点的边为 关键边，注意到不合法的方案至少包含一条关键边，且不同的关键边方案对应的一定是不同的方案，故可以按关键边数量容斥。

设这条边上有 $a$ 个顶点（不含两端），$f_i$ 表示剩下 $i$ 个顶点（不含两端）的方案数。枚举选中了 $k$ 个点，插板可得：

$$f_i=\sum\limits_{k=i}^a (-1)^{k-i} \dbinom{a}{k} \dbinom{i+1}{k-i}$$

最后只需要将所有 $F_a(x)$ 乘起来再乘上对应的卡特兰数统计答案即可。接下来考虑如何快速计算 $F_a(x)$。

$$f_i=[x^{a-i}] \sum\limits_{k=i}^{a} \dbinom{a}{k} x^{a-k} \dbinom{i+1}{k-i} (-x)^{k-i}$$

$$f_i=[x^{a-i}] (1+x)^a (1-x)^{i+1}$$

记 $G_k(x)=(1+x)^a (1-x)^k$。注意到 $G_k(x)$ 是 D-finite 的，对其求导：

$$G_k'(x)=G_k(x) (\dfrac{a}{1+x}-\dfrac{k}{1-x})$$

$$(1-x^2)G_k'(x)=a(1-x)G_k(x)-k(1+x)G_k(x)=(a-k)G_k(x)-(a+k)xG_k(x)$$

$$(i+1)g_{i+1}=(a-k)g_i-(k+a-i+1)g_{i-1}$$

于是记录相邻两项系数，可以 $O(1)$ 推出前后项。

同时有 $G_{k+1}(x)=(1-x)G_k(x)$，故可以推出 $G_k(x)$ 的三项，再推出 $G_{k+1}(x)$ 的两项。

类似莫队转移，可以 $O(a)$ 计算出 $F_a(x)$。该部分总时间复杂度 $O(\sum a_t)$。

总时间复杂度 $O(\sum a_t \log^2 \sum a_t)$。

LOJ3397「2020-2021 集训队作业」春天，在积雪下结一成形，抽枝发芽

析合树的构成具有以下性质：

• 析点的儿子全为合点。

• 合点的合点儿子必须反向。

设有 $i$ 个叶子节点，根节点为析点的菊花形析合树的数量为 $f_i$，根节点为合点的数量的析合树数量为 $2g_i$（即只统计单调上升），排列的生成函数为 $H(x)$（无常数项）。

由上述性质，对应到生成函数上即为：

$$G(x)=\sum\limits_{i \geq 2} (H(x)-G(x))^i=\dfrac{1}{1-H(x)+G(x)}-1-H(x)+G(x)$$

$$F(H(x))=H(x)-2G(x)-x$$

由第一条式子，

$$(1+H(x))(1-H(x)+G(x))=1$$

$$G(x)=\dfrac{H^2(x)}{1+H(x)}$$

设 $R(x)$ 为 $H(x)$ 的复合逆，代入得 $G(H(x))=\dfrac{x^2}{1+x}$。再代入第二条式子：

$$F(x)=x-\dfrac{x^2}{1+x}-R(x)$$

于是只需计算 $R(x)$ 即可。

同 LOJ2554「CTSC2018」青蕈领主，使用分治 NTT，时间复杂度 $O(n \log^2 n)$。

CF1691F K-Set Tree (2500)

拆贡献，考虑在以 $r$ 为根时 $x$ 没有贡献当且仅当将 $r$ 到 $u$ 的链删掉后，所有选出的点都在剩下的一棵子树内。算出方案数后用总数减掉即为答案。

不换根。若枚举每个 $x$ 难以统计删链后的子树信息，直接考虑每棵子树的贡献。下面设 $fa$ 为 $u$ 的父亲，有两种情况：

• 以 $u$ 为根的子树，则要求链经过 $fa$ 且不经过 $u$。不合法的情况即为 $x$ 和 $r$ 都在以 $fa$ 为根的同一棵子树内（且不在以 $u$ 为根的子树内）。

• 以 $u$ 为根的子树补，则要求链经过 $u$ 且不经过 $fa$。不合法的情况即为 $x$ 和 $r$ 都在以 $u$ 为根的同一棵子树内（且不在以 $u$ 为根的子树补内）。

预处理每个点的子树大小 $siz_u$ 及 $f_u$ 表示删掉 $u$ 后在剩下的某棵子树内选 $k$ 个点的方案数。则容易计算上述方案数，总时间复杂度 $O(n)$。

CF1667E Centroid Probabilities (3000)

设点 $k$ 子树大小超过 $(n-1)/2$ 的方案数为 $f_k$。由于重心是唯一的，故点 $k$ 为重心的方案数为 $(n-1)!-f_k-\sum\limits_{i=k+1}^n \dfrac{1}{i-1} f_i$。只需要快速计算 $f_k$ 即可。

枚举 $f_k$ 的子树大小为 $i$，有：

$$f_k=(k-1)! \sum\limits_{i=(n+1)/2}^{n-k} \dbinom{n-k}{i-1} (i-1)! \dfrac{(n-i-1)!}{(k-2)!}=\dfrac{(n-k)!}{k-2} \sum\limits_{i=(n+1)/2}^{n-k} \dfrac{(n-i-1)!}{(n-k-i+1)!}$$

$$f_k=\dfrac{(n-k)!}{k-2} \sum\limits_{i=(n+1)/2}^{n-k} (n-i-1)^{\underline{k-2}}$$

而后面这个东西就是有限积分（或叫整数裂项），可以这样算：

$$\sum\limits_{i=k}^n i^{\underline k}=\dfrac{1}{k} (n+1)^{\underline k}$$

总时间复杂度 $O(n)$。

CF1672G Cross Xor (3200)

首先肯定要分析能被操作到的矩阵的性质。

将所有合法矩阵写成 $nm$ 维的向量，构成线性空间 $M$。

记在初始网格上操作 $(x,y)$ 后得到的向量为 $P_{x,y}$，显然 $M$ 中元素都可以由 $\{P_{x,y}\}$ 线性组合出，但仍难以分析。

考虑 $M$ 的正交补空间 $M^{\perp}$。注意到 $P_{x_1,y_1} \oplus P_{x_1,y_2} \oplus P_{x_2,y_1} \oplus P_{x_2,y_2} \in M$，其影响是只将 $(x_1,y_1),(x_1,y_2),(x_2,y_1),(x_2,y_2)$ 反转，故若 $u \in M^{\perp}$，则：

$$\forall x_1,x_2,y_1,y_2, u_{x_1,y_1} \oplus u_{x_1,y_2} \oplus u_{x_2,y_1} \oplus u_{x_2,y_2}=0$$

也就是说，若固定两行 $x_1,x_2$，则 $\forall y_1,y_2,u_{x_1,y_1} \oplus u_{x_2,y_1} = u_{x_1,y_2} \oplus u_{x_2,y_2}$，即存在常数 $c$ 使 $u_{x_2,y}=u_{x_1,y} \oplus c$。进一步可知这等价于存在 $n$ 维向量 $A$ 及 $m$ 维向量 $B$ 使得 $u_{x,y}=A_x \oplus B_y$。

考虑如何判断 $(A,B)$ 生成的 $u$ 是否合法。由于 $M$ 中元素都可以由 $\{P_{x,y}\}$ 线性组合出，只需要判断 $u$ 是否与所有 $P_{x,y}$ 垂直即可。即：

$$\forall x,y,u \cdot P_x,y=(\oplus A_i) \oplus (\oplus B_i) \oplus (m-1)A_x \oplus (n-1)B_y=0$$

显然与 $n,m$ 的奇偶性有关，分情况讨论：

• $n,m$ 均为偶数：条件变为 $A_x \oplus B_y=(\oplus A_i) \oplus (\oplus B_i)$。

  故 $A_x,B_y$ 都是常数且相等，生成的 $u$ 每一位都为 $0$。

  即所有方案合法。

• $n$ 为偶数，$m$ 为奇数：条件变为 $B_y=(\oplus A_i) \oplus (\oplus B_i)$。

  故 $B_y$ 是常数且 $\oplus A_i=0$。生成的 $u$ 每一行的元素都相同。考虑 $v \in M$，若将 $u$ 中某全 $1$ 行与某全 $0$ 行互换，那么 $v$ 中这两行的异或和必须相同。进一步得到 $v$ 合法当且仅当每一行的异或和相同。

  即每一行的异或和相同的方案合法。

• $n$ 为奇数，$m$ 为偶数：每一列的异或和相同的方案合法。

• $n,m$ 均为奇数：条件变为 $(\oplus A_i) \oplus (\oplus B_i)=0$。

  同上面的分析，$v$ 合法当且仅当每一行每一列的异或和相同。

  即每一行每一列的异或和相同的方案合法。

---

考虑计数。

• $n,m$ 均为偶数：答案为 $2^{\#_{?}}$。

• $n$ 为偶数，$m$ 为奇数：枚举每一行的异或和。若该行没有 $?$ 则异或和已经确定，否则若有 $c$ 个 $?$ 则方案数为 $2^{c-1}$。

• $n,m$ 均为奇数：先枚举每一行每一列的异或和。一个元素会影响到一行及一列，可以考虑将行列看作点，元素看作边建图。

  先统计每一行每一列与目标状态的异或和作为权值。对于每一个联通块，若所有点权值异或和不为 $0$ 则无解（连边不改变奇偶性），否则若有 $V$ 个点 $E$ 条边则方案数为 $2^{E-V+1}$（这是因为随意求出一棵生成树并确定非树边情况后，树边情况是唯一的）。

时间复杂度 $O(nm)$。

UOJ683 【UR #22】月球车站

记 $0$ 表示反面，$1$ 表示正面，$c_x$ 表示状态 $x$ 的第一个硬币，$tr_{x,1},tr_{x,0}$ 分别表示 $x$ 选择是否反转的后继状态。则可以列出经典期望 DP：

$$f_x=1+pf_{tr_{x,1}}+(1-p)f_{tr_0},c_x=0$$

$$f_x=1+\max\{f_{tr_{x,0}},f_{tr_{x,1}}\},c_x=1$$

这东西成环还带 $\max$，不是很可做。

---

分析性质尝试把环和 $\max$ 去掉。假设伏特采用最优策略使步数尽可能少，即 $f_x=1+\min\{f_{tr_{x,0}},f_{tr_{x,1}}\},c_x=0$。

类似 Dijkstra 从终止状态倒推。设当前考虑状态 $u$，$u$ 能转移到的两个状态分别为 $x,y$（其中 $c_x=0,c_y=1$ 且它们除了第一个硬币外都相同）。

若 $x$ 是第一次被访问到，则可以直接转移（伏特希望步数尽可能少）；若 $y$ 是第二次被访问到，那么只能转移（$y$ 第一次访问不会被转移，而每个点只会转移到两个状态，第二次转移即为较大的那个）。

又注意到 $x$ 和 $y$ 除了第一个硬币外都相同，它们被访问到的次数是相同的，故每次拓展恰有一个状态被转移。也即转移形成一条链。

这里有一个不严谨之处：初始状态（即全为正面）无法作为第二次转移的 $y$，从而导致提前终止，某些状态没有被转移到。下面证明所有情况伏特都能使游戏在有限步内结束：

证明：称 $n$ 次操作为一回合。在每一回合内，伏特先始终翻转，如果 skip 蚤始终不翻转，这一回合后就会结束；否则，在 skip 蚤第一次翻转后伏特将策略改为始终不翻转，这样一回合后状态倒序的字典序都会严格减小，于是游戏能在有限次操作内结束。

---

回到原问题，先将所有状态按照链上顺序编号（$f_i$ 的编号也对应改变）。伏特每次操作会从 $u$ 跳到 $u-1$ 或 $x>u-1$，skip 蚤每次操作会从 $u$ 跳到 $u-1$ 或 $x<u-1$。

环差不多已经去掉了，考虑去 $\max$，有结论：$f_i$ 单调递增。

证明：若 $x<y,f_x>f_y$，skip 蚤从 $y$ 到 $x$ 过程中每次都从 $u$ 跳到 $u-1$，第一次到达 $x$ 后按 $f_x$ 最优策略走。这个策略的步数 $f_y'>f_x>f_y$，与 $f_y$ 的最大性矛盾。

于是去掉了 $\max$。现在转移形如 $u \rightarrow u-1$ 或 $u \rightarrow x,x>u-1$。同 P6835 [Cnoi2020]线形生物，将状态改为 $u$ 到 $u-1$ 的期望步数即可线性解决。

$p=0$ 或 $p=1$ 时可能无解，需要特判。

时间复杂度 $O(2^n)$。

CF1603F October 18, 2017 (2700)

《2700》

显然只关心 $x$ 是否为 $0$，因为若 $x>0$ 可以通过变换基底化为同种情况。

• $x=0$ 时，即要求 $n$ 个向量线性无关，方案数即 $\prod\limits_{i=0}^{n-1} (2^k-2^i)$。

• $x>0$ 时，枚举维度为 $r$。

先计算基底的数量。要求不能线性组合出 $x$ 的限制比较难处理，考虑用总数减去反面。

可以从整体考虑：一组基底共可以组合出 $2^r-1$ 个非零向量，而所有 $2^k-1$ 个非零向量出现的概率是均等的，故能组合出 $x$ 的基底数量即为：

$$\dfrac{2^r-1}{2^k-1} \prod\limits_{i=0}^{r-1} (2^k-2^i)=(2^r-1) \prod\limits_{i=1}^{r-1} (2^k-2^i)$$

于是不能组合出 $x$ 的基底数量为：

$$\prod\limits_{i=0}^{r-1} (2^k-2^i)-(2^r-1) \prod\limits_{i=1}^{r-1} (2^k-2^i)=(2^k-2^r)\prod\limits_{i=1}^{r-1} (2^k-2^i)=\prod\limits_{i=1}^{r} (2^k-2^i)$$

还要计算剩下 $n-r$ 个元素的数量。同 ARC133F Many Xor Optimization Problems，写出生成函数：

$$[x^{n-r}] \prod\limits_{i=0}^{r} \dfrac{1}{1-2^ix}=\dbinom{n}{r}_2$$

于是答案即为：

$$Ans=\sum\limits_{r=0}^n \dbinom{n}{r}_2 \prod\limits_{i=1}^{r} (2^k-2^i)$$

预处理后即可 $O(\min(n,k))$ 计算。

P7213 [JOISC2020] 最古の遺跡 3

容易发现原过程等价于以下过程：

从大到小枚举每个 $i$，不断进行：若存在 $j>i$ 使 $a_j=a_i$ 则令 $a_i \leftarrow a_i-1$。

那么也等价于以下过程：

维护一个桶 $\{b_i\}$，从后往前考虑每个 $a_i$，找到最大的数 $x \leq a_i$ 使得 $b_x=0$，如果 $x>0$ 则令 $b_x=1$。

先认为 $2n$ 个数互相区分，最后再除以 $2^n$ 即可。将从后往前改为从前往后，本质不变。

考虑维护数组 $\{c_i\}$，$c_i$ 表示剩下的数中填入后会变成 $i$ 的数字数量。每次操作为以下两种之一：

• 选中一个 $k>0$，找到最大的 $x \leq k$ 使得 $c_x \neq 0$（如果找不到则 $x=0$），然后令 $c_x \leftarrow c_x+c_k-1,c_k \leftarrow 0$。（对应石柱最后变为 $k$）

• 如果 $c_0>0$，可以令 $c_0 \leftarrow c_0-1$。（对应石柱消失）

那么记 $dp_{i,j}$ 表示填了 $i$ 个数，$c_1,\cdots,c_j =0$ 且 $c_{j+1} \neq 0$ 的方案数。

转移考虑：

• $k \neq j+1$ 时，算做一个无用步数，转移系数为 $1$（可以用 $i$ 和 $j$ 可以算出 $c_0$）。

• $k=j+1$ 时，枚举之前已经填好了 $j+2 \sim t$，那么从前面的无用步数（设为 $d$，也可以用 $i$ 和 $j$ 算出）中取出 $t-j-1$ 步用来填 $j+2 \sim t$（假设方案数是 $pre_{t-j-1}$），那么可以得到转移系数为 $\dbinom{d}{t-j-1} pre_{t-j-1} (t-j+1)$。

注意到 $pre_i$ 相当于没有石柱消失的方案数，再做一次 DP 预处理出来即可。

总时间复杂度 $O(n^3)$。

事实上转移式就是个卷积式，可以 NTT 优化到 $O(n^2 \log n)$。

LOJ3394 「2020-2021 集训队作业」Tour

先考虑 $a_i \geq 0$ 的情况。考虑以下算法：

• 维护可重集 $S=\{a_1,a_2,\cdots,a_n\}$ 与变量 $s$ 表示能放的位置数量。

• 不断执行以下操作：令 $ans \leftarrow ans \cdot s=1$，记 $x,y$ 分别为 $S$ 中最小值与最大值。

  • 若 $xy \leq w$，则 $x$ 与之后填的任何数均可以相邻。从可重集中删掉 $x$，并令 $s \leftarrow s+1$（用掉一个位置，新增两个位置）。

  • 若 $xy > w$，则 $y$ 与之后填的任何数均不能相邻。从可重集中删掉 $y$，并令 $s \leftarrow s-1$（用掉一个位置）。

时间复杂度 $O(n)$。

回到原题目，只需要考虑每个极长连续符号相同段。求出将自然数/负数填进 $k$ 段的方案数 $f_i/g_i$，答案即为 $\sum\limits_{i=0}^{\min(n,m)} (2f_ig_i+f_ig_{i-1}+f_{i-1}g_i)$。

以自然数为例。记上述算法中 $s-1$ 的值依次为 $p_0,p_1,p_2,\cdots,p_n$，有：

$$f_t=\prod\limits_{i=0}^{n-1} (t+p_i)$$

可以直接分治乘再多点求值做，常数很大。

更好的做法是分治下降幂卷积，下降幂多项式容易转成点值。

总时间复杂度 $O(n \log^2 n)$，常数较大。

P8554 心跳

组合对象符号化板题

%%%粉兔

考虑序列中所有前缀最大值 $x_1,x_2,\cdots,x_k$，以它们为左端点将原序列划分为 $k$ 段。

考虑每一段 $[l,r]$ 内的 $a_i$ 取值，显然 $a_{l+1}=\cdots=a_r=k$，而对于 $a_l$ 有结论：

总可以通过排列 $p_{l+1},\cdots,p_r$，使得 $a_l$ 取到 $[k,k+r-l]$ 的所有值。如果 $l > 1$，还可取到 $k-1$。

记 $b_i=a_i-k$，那么每一段一定是 $[-1],[0,0],[1,0,0],\cdots$ 中的一个接若干个 $0$。

注意到不同的 $\{b_i\}$ 一定对应不同 $\{a_i\}$，下面考虑计数 $(\{b_i\},k)$。

考虑对某个 $\{b_i\}$，$k$ 的取值为连续区间 $[L,R]$。设 $h_{n,i}$ 表示 $k$ 能取到 $i$ 的 $\{b_i\}$ 数量。下面求 $f_{n,i},g_{n,i}$ 分别表示 $L=i$ 或 $R=i$ 的 $\{b_i\}$ 个数。则有 $h_{n,i}=\sum\limits_{j=1}^i f_{n,j}-\sum\limits_{j=1}^{i-1} g_{n,j}$。

......

TopCoder 14563S RM717 Div1B DerangementsStrikeBack

先考虑如何计算错排数。

无自环环排列的指数型生成函数是：

$$F(x)=\sum\limits_{i \geq 2} (i-1)! \dfrac{x^i}{i!}=-\ln(1-x)-x$$

那么错排即无自环环排列的自由组合，即：

$$G(x)=\exp{F(x)}=\dfrac{e^{-x}}{1-x}$$

是 D-finite 的，可以化成整式递推 $O(n)$ 计算。

回到原问题，设现在计算 $k$ 的答案。考虑先填 $1 \sim k$ 的数，那么剩下的数可以随意填，方案数即 $n!$。

若由每个 $i$ 向 $p_i(p_i \leq k)$ 连边，那么会形成若干形如 $v_1>k,v_2 \leq k,\cdots,v_m \leq k$ 的链即若干非自环的环。考虑按以下方式计数：

• 对于每个 $i > k$，选择集合 $S_i \in \{1,\cdots,k\}$。所有 $S_i$ 两两不交。

• 对于每个 $i > k$，安排 $S_i$ 中元素的顺序以形成一条链，方案数为 $|S_i|!$。

• 对于不在任何 $S_i$ 中出现的元素 $t \leq k$，形成错排，方案数为 $D_{n-\sum_{i=k+1}^n |S_i|}$。

写成生成函数即：

$$H(x)=(\sum\limits_{i \geq 0} i! \dfrac{x^i}{i!})^n G(x)=\dfrac{e^{-x}}{(1-x)^{n+1}}$$

也是 D-finite 的，可以化成整式递推：

$$H'(x)=\dfrac{n+x}{1-x} H(x)$$

$$h_k=\dfrac{(n+k-1)h_k+h_{k-1}}{k}$$

总时间复杂度 $O(m)$。

*可能更快(dai)速(shu)的做法：容斥后再写成生成函数。

2020ICPC 济南 H Path Killer

类似 ABC242Ex Random Painting，停时期望等于所有非法状态 出现的概率 乘上 离开该状态期望时间 的和。

只需要对每个 $k$ 求出选中 $k$ 个点没有覆盖所有路径的方案数即可，容斥变为覆盖所有路径的方案数。

设 $f_{u,i,j}$ 表示考虑 $u$ 的子树，还未覆盖的路径向上延申的长度为 $i$，已经选了 $j$ 个点的方案数。先树形依赖背包合并，再枚举当前点是否选转移。

暴力转移复杂度 $O(n^5)$。注意到第二维是 $\min$ 卷积，第三维是树形依赖背包，故可优化至 $O(n^3)$。

*使用 Min-Max 容斥可以做到同样复杂度，虽然一般这两种方法貌似不能同时使用。

SPOJ-RNG Random Number Generator | HDU6309 Absolute

对于定义在 $\mathbb{R}$ 上的函数 $f(x),g(x)$，定义连续卷积为定义在 $\mathbb{R}$ 上的函数 $h(x)$，对所有 $x \in \mathbb{R}$ 满足：

$$h(x)=\int_{-\infty}^{\infty} f(t) g(x-t) dt$$

若 $f(x),g(x)$ 均为分段函数且每一段为低次多项式，可以考虑这样求解：

枚举 $f(x)$ 中的每一段 $\forall x \in [l,r],f(x)=F(x)$，$g(x)$ 中的每一段 $\forall x \in [L,R],g(x)=G(x)$，其中 $F(x),G(x)$ 分别为 $d1,d2$ 次多项式。

下面假设 $r+L \leq l+R$，否则交换 $F(x),G(x)$。

计算二元多项式 $s(t,x)=f(t)g(x-t)$，关于 $t$ 求 $s(t,x)$ 的不定积分 $S(t,x)=\int s(t,x) dt+C$。

对于某个 $x$，$t$ 需要满足 $l \leq t \leq r \wedge L \leq x-t \leq R$。对 $t$ 的取值区间进行分类讨论：

• 当 $x \in [l+L,r+L]$ 时，$t \in [l,x-L]$，故 $h(x)=S(x-L,x)-S(l,x)$。
• 当 $x \in [r+L,l+R]$ 时，$t \in [l,r]$，故 $h(x)=S(r,x)-S(l,x)$。
• 当 $x \in [l+R,r+R]$ 时，$t \in [x-R,r]$，故 $h(x)=S(r,x)-S(x-R,x)$。

以上所有操作均可以在 $O((d1+d2)^3)$ 时间内完成，同时注意到若设 $f(x)$ 共 $n$ 段，$g(x)$ 共 $m$ 段，则分段端点至多只有 $(n-1)(m-1)$ 个。故可以利用差分与前缀和在 $O(nm(d1+d2)^3)$ 内计算 $h(x)$。

注意到 $h(x)$ 内每一段的次数不高于 $d1+d2+1$，故若计算 $n$ 个函数 $f_1(x),f_2(x),\cdots,f_n(x)$ 的连续卷积，设其次数分别为 $d_1,d_2,\cdots,d_n$，段数分别为 $k_1,k_2,\cdots,k_n$，则可以在 $O(\prod (k_i+1) (\sum d_i+n)^3)$ 内计算其连续卷积。

直接计算 $n$ 个 $0$ 次多项式的连续卷积 $h(x)$（即答案的概率密度函数）。

对于 RNG，对 $h(x)$ 每一段 $[A,B]$ 内的部分进行积分求和即可。

对于 ABS，对 $h(x)$ 每一段乘上 $x$ 再积分求和即可。

总时间复杂度 $O(n^3 2^n)$。

QOJ5031 2022集训队互测 核

先考虑如何对某个 $B$ 求 $f(B)$。注意到 $A$ 的每一行相互独立，设 $A$ 中某一行为向量 $\bold{a}$，则 $\bold{a}$ 需要满足：

$$\bold{a} B=\bold{a}$$

即 $\bold{a}$ 为 $B$ 的特征值为 $1$ 对应的特征向量。那么设 $B$ 特征值为 $1$ 对应的特征子空间 $V_1$ 维数为 $d$，则 $\bold{a}$ 的方案数为 $q^d$。

下面对每个 $k \in [0,n]$ 求出 $V_1$ 维数为 $k$ 的矩阵（或视为线性变换）$B$ 个数 $f_k$。

考虑容斥，设钦定 $V_1$ 至少 $k$ 维的矩阵 $B$ 个数为 $g_k$，于是有：

$$g_k=\sum\limits_{i=k}^n \dbinom{i}{k}_q f_i$$

这是因为考虑 $f_i$ 对 $g_k$ 的贡献，相当于在 $k$ 维空间中选出 $i$ 维子空间，方案数为 $\dbinom{i}{k}_q$。

考虑如何计算 $g_k$，先从 $n$ 维空间中选出 $k$ 维空间钦定为特征子空间（这 $k$ 维的线性变换就确定了），方案数为 $\dbinom{n}{k}_q$；再对剩下的 $n-k$ 维确定一个满秩的线性变换，方案数为 $\prod\limits_{i=k}^{n-1} (q^n-q^i)$。于是：

$$g_k=\dbinom{n}{k}_q \prod\limits_{i=k}^{n-1} (q^n-q^i)$$

由子空间反演，得：

$$\begin{aligned} f_k &=\sum\limits_{i=k}^n (-1)^{i-k} q^{\binom{i-k}{2}} \dbinom{i}{k}_q g_i\\ &=\sum\limits_{i=k}^n (-1)^{i-k} q^{\binom{i-k}{2}} \dbinom{i}{k}_q \dbinom{n}{i}_q \prod\limits_{t=i}^{n-1} (q^n-q^t)\\ &=\sum\limits_{i=k}^n (-1)^{i-k} q^{\binom{i-k}{2}} \dbinom{n}{k}_q \dbinom{n-k}{i-k}_q \prod\limits_{t=i}^{n-1} (q^n-q^t)\\ &=\dbinom{n}{k}_q \sum\limits_{i=0}^{n-k} (-1)^{i} q^{\binom{i}{2}} \dbinom{n-k}{i}_q \prod\limits_{t=i+k}^{n-1} (q^n-q^t)\\ &=\dbinom{n}{k}_q \sum\limits_{i=0}^{n-k} (-1)^{n-k} q^{\binom{i}{2}} \dbinom{n-k}{i}_q q^{\binom{n}{2}-\binom{i+k}{2}} (q;q)_{n-i-k}\\ &=\dbinom{n}{k}_q (-1)^{n-k} (q;q)_{n-k} q^{\binom{n}{2}-\binom{k}{2}} \sum\limits_{i=0}^{n-k} q^{-ik} \dfrac{1}{(q;q)_i}\\ \end{aligned}$$

记 $h_k=\sum\limits_{i=0}^{k} q^{-(n-k)i} \dfrac{1}{(q;q)_i}$，考虑 $h_{k+1}$：

$$\begin{aligned} h_{k+1} &=\sum\limits_{i=0}^{k+1} q^{-(n-k-1)i} \dfrac{1}{(q;q)_i}\\ &=\sum\limits_{i=0}^{k+1} q^{-(n-k)i} \dfrac{1}{(q;q)_i} [1-(1-q^i)]\\ &=\sum\limits_{i=0}^{k+1} q^{-(n-k)i} \dfrac{1}{(q;q)_i} - \sum\limits_{i=1}^{k+1} q^{-(n-k)i} \dfrac{1}{(q;q)_{i-1}}\\ &=h_k+q^{-(n-k)(k+1)} \dfrac{1}{(q;q)_{k+1}}-q^{-(n-k)} h_k\\ &=(1-q^{-(n-k)})h_k+\dfrac{q^{-(n-k)(k+1)}}{(q;q)_{k+1}}\\ \end{aligned}$$

$h_k$ 可以线性递推，于是可以在 $O(n)$ 内求出所有 $f_k$。

还有一个小问题：如何快速计算 $\sum\limits_{k=0}^n f_k 3^{q^{kn}}$？

设 $B=\lceil \sqrt{mod} \rceil$，对每个 $i \in [0,B)$ 预处理出 $3^i$ 及 $3^{Bi}$，计算幂时直接查询即可。

总时间复杂度 $O(n+\sqrt{mod})$。