Atcoder 计数乱做

ARC132E Paw (3100)

记覆盖为左为 <-，覆盖为右为 ->，不覆盖为 =。则最后一定变成 <<<...===...>>>，且等号两侧是两个相邻的洞。

考虑对每两个相邻的洞算最后形成这种情况的概率。设左边有 $L$ 个洞，右边有 $R$ 个洞。

显然左右是独立的，只考虑右边。那么只要求每次选择时，如果选到最左的，不能向左走。即有：

$$F_n=(1-\dfrac{1}{2n})F_{n-1}=\sum\limits_{i=1}^n \dfrac{2i-1}{2i}$$

概率即为 $F_lF_r$。

时间复杂度 $O(n)$。

ARC132F Takahashi The Strongest (3000)

发现 T 能赢 A 和 S 当且仅当 A 和 S 出一样的，而 T 比他们俩都大。

考虑把给出的策略扔进四元幂级数里，然后做以下运算的卷积：

$$x \otimes y= \begin{cases} x,x=y\\ 3,x \neq y \end{cases}$$

由 FWT 理论，构造变换矩阵：

$$\left[ \begin{matrix} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$$

太好看了，所以随便求出逆矩阵：

$$\left[ \begin{matrix} 1 & 0 & 0 & -1\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$$

求出卷积 $F$ 后翻转一下，现在只需要对每一个集合求 $F$ 中与它至少有一位相同的集合数量。

容斥一下，变成每一位都不同，可以再 FWT。

总时间复杂度 $O(k4^k)$。

ABC225H Social Distance 2 (3000)

先考虑 $K=0$，并且要对三种情况分别算 $S1(n,m)$，$S2(n,m)$，$S3(n,m)$，分别是：

• 两旁都坐人
• 左边坐人，右边无人
• 两旁都无人

用一些简单的生成函数可以推导出分别是 $\dbinom{n+k-1}{2k+1}$，$\dbinom{n+k-1}{2k}$，$\dbinom{n+k-1}{2k-1}$。

最后分治 FFT 卷到一起即可。

时间复杂度 $O(n \log^2 n)$。

ARC101F Robots and Exits (2900)

经过 114514 分钟思考后，记 $L_i$ 与 $R_i$ 分别为第 $i$ 个机器人到最近左右出口的距离。

注意到方案仅在于每个机器人是从左还是右出口离开。并且如果机器人不消失的话，向左和向右是相对独立的。也就是过程一定是向左走一段，再向右走一段……

按 $L_i$ 排序，再设单调不降的数组 $P_i$，那么过程可以看作向左走 $L_1$，再向右走 $P_1$，再向左走 $L_2$，再向右走 $P_2$……

最后若 $P_i \geq R_i$，那么机器人 $i$ 就从左出口离开；否则从右出口离开。

现在问题被简化了许多，考虑对 $R_i$ DP。设 $dp_i$ 表示 $P_i=R_i$ 且 $P_{i-1}<R_i$ 的方案数。

$$dp_i=\sum\limits_{0 \leq j<i \wedge R_j<R_i} dp_j$$

注意 $dp_0=1$。

然而这样不太正确，原因在于某些机器人的 $L$ 相同，它们的 $P$ 也必须相同，这样后面就会算重（因为只需加一次）。

解决办法很简单，如果 $L_i=L_{i-1}$ 的话，就做个差分即可。

二维偏序用树状数组优化，时间复杂度 $O(n \log n)$。

AGC032F One Third (4000)

考虑转化问题。认为操作是在圆周上画红点，并且每画一个红点就在顺时针 $120^\circ$ 位置画一个绿点，在逆时针 $120^\circ$ 位置画一个蓝点。

于是问题变为了两个异色点间最短距离期望。

按第一次画点断环为链，问题变为：

一根长度为 $[0,\dfrac{1}{3}]$ 的线段的左端点为红点，右端点为蓝点。随机位置随机颜色画 $n-1$ 个点，求两个异色点最短距离期望。

显然最短的异色点对一定是相邻的，考虑枚举相邻异色点对数 $k$，再计算概率和条件期望相加即可。

• 概率：只考虑同色连续段，这样相邻两个点一定异色。设以 R 开头，B 结尾的方案数为 $f_n$，以 R 结尾的方案数为 $g_n$，则 $f_n=f_{n-1}+g_{n-1},g_n=2f_{n-1}$。最后再插板乘上 $\dbinom{n}{k}$ 即可。

• 条件期望：异色点对连成的线段总长度期望为 $\dfrac{k}{3n}$，由随机变量相关理论可知最短期望为 $\dfrac{1}{k^2} \times \dfrac{k}{3n}=\dfrac{1}{3nk}$。

时间复杂度 $O(n)$。

ABC236Ex Distinct Multiples (2900)

显然唯一难搞的就是 “互不相同” 条件，直接考虑容斥。

也许会考虑钦定一些点填的数必须相同，但这样需要记录若干组点集，难以实现。

不妨考虑钦定边集（两个点填的数相同即连边）。设 $f_S$ 表示恰好连 $S$ 边的方案数，$g_S$ 表示钦定连 $S$ 边的方案数。

显然 $g_S=\sum\limits_{T \supseteq S} f_T$，由子集反演得 $f_{\varnothing}=\sum\limits_{S} (-1)^{|S|} g_S$。

由于边集太大，我们无法直接枚举 $S$ 计算。但 $g_S$ 只与连接 $S$ 后分成的若干联通块的点集有关，可以考虑枚举点集。$g_S$ 即为若干联通块的方案数相乘，可以对每个联通块分别考虑，最后直接子集卷积 $\exp$ 即可。

现在枚举 $n$ 个点的点集 $V$，考虑其中所有使 $V$ 联通的边集 $S$ 的权值（即 $(-1)^{|S|}$）之和，设其为 $P_n$。

设 $Q_{n,k}$ 表示 $n$ 个点的点集，$k+1 \sim n$ 的每个点都要与 $1 \sim k$ 中某个点联通的权值之和。

• 当 $k>1$ 时，考虑 $1$ 号点与 $2$ 号点，它们间连边与不连边的权值正好相反，于是 $Q_{n,k}=0$。

• 当 $k=1$ 时，考虑 $n$ 号点连出的边有 $t$ 条，方案数为：

$$Q_{n,1}=(-1)\sum\limits_{t=1}^{n-1} \dbinom{n-1}{t} Q_{n-1,t}=-(n-1)Q_{n-1,1}$$

故 $P_n=(-1)^{n-1} (n-1)!$。

总时间复杂度 $O(n^2 2^n)$。

AGC044 Random Pawn (3600)

设 $f_i$ 表示出生在 $i$ 号点，最优策略下的期望分数，显然有转移式：

$$f_i=\max\{A_i,\dfrac{1}{2}(f_{i-1}+f_{i+1})-B_i\}$$

然而我们并不知道转移顺序。仔细观察，不妨设 $A_1$ 为 $A_i$ 中的最大值，由于所有 $f_i \leq A_1$，可得$f_1=A_1$。可以以此断环为链（新开与 $1$ 号点相同的 $n+1$ 号点）。

然而剩下的仍不知道转移顺序。但是观察发现如果 $B_i=0$，事实上只需要求出所有 $(i,A_i)$ 构成的上凸壳，即可算出答案。

尝试做一些转换使原问题变为 $B_i=0$。令 $g_i=f_i-C_i$，则：

$$g_i+C_i=\max\{A_i,\dfrac{1}{2}(f_{i-1}+f_{i+1}+g_{i-1}+g_i)-B_i\}$$

$$g_i=\max\{A_i-C_i,\dfrac{1}{2}(f_{i-1}+f_{i+1})+\dfrac{1}{2}(g_{i-1}+g_i)-B_i-C_i\}$$

我们希望对于所有 $i \in [2,n]$，$\dfrac{1}{2}(g_{i-1}+g_i)-B_i-C_i=0$，即 $C_{i+1}=2B_i+2C_i-C_{i-1}$。

待定系数，设 $C_1=0$，$C_2=k$，依次递推出 $C_{n-1}=pk+q$ 与 $C_{n}=p'k+q'$ 即可算出 $k=\dfrac{2B_n-q+2q'}{p-2p'}$。

时间复杂度 $O(n)$。

ARC134F Flipping Coins (3500)

显然 $i$ 只会影响 $p_i$，因此把排列拆成若干循环，循环间互相独立。接下来考虑计算循环方案数的生成函数，最后 $\exp$ 即可得到答案。

对于每个循环，再分成若干条极长单调递增的链（有序），称每条链的链尾为“坏的”（即满足 $p_i<i$ 的点），则最后向上的硬币数量就是坏点被操作的次数。

设每条链的生成函数为 $F(x)=\sum\limits_i W^{i \bmod 2}x^i$，然而大力卷会算重。

我们发现不满足限制（即不是极长的）的两条链可以组成一条更长的链，尝试容斥，然而链的长度带权，无法直接容斥。

考虑一种神奇的做法：我们不直接容斥，而是给每个长度赋一个新的权，其生成函数为 $A(x)$，再使 $A$ 以任意方式组合起来后恰好为正确的方案数：

$$\dfrac{1}{1-A(x)}=F(x)$$

$$A(x)=1-\dfrac{1}{F(x)}$$

而答案的生成函数为：

$$\hat S(x)=\exp[\sum\limits_{i} \dfrac{\hat A(x)^i}{i!} (i-1)!]=\dfrac{1}{1-\hat A(x)}$$

设 $G(x)=\dfrac{1}{F(x)}$，则 $\hat S(x)=\dfrac{1}{\hat G(x)}$。

只需要多项式求逆甚至不需要卷积，时间复杂度 $O(n\log n)$。

一句话题解：多项式求逆

ARC133E Cyclic Medians (3300)

众所周知 $E(X)=\sum\limits_{i \geq 0} P(i>X)$。设最后结果为 $a$，考虑枚举 $k$，算 $a>k$ 的方案数。

记 $>k$ 的数为 $1$，$\leq k$ 的数为 $0$。则若 $x_i=y_j$，则 $a$ 会改变；否则不变。

考虑 $a$ 在过程中是否改变（遇到 $x_i=y_j$ 即认为改变）。

• 对于改变的情况，$a$ 与 $A$ 无关，故 $k=p,a=id$ 及 $k=V-p,a=1-id$ 的方案数是一样的（即对称），直接除 $2$ 即可。用总方案数减去不变情况数即为改变情况数。

• 对于不变的情况，$x$ 及 $y$ 十分有限。设 $g=\gcd(x,y)$，则 $a$ 会经过每一对 $(x,y)$ 满足 $x \equiv y \pmod g$。故 $x_i=x_{i+tg}$，$y_i=y_{i+tg}$ 且 $x_i \neq y_i$（否则一定会有 $x_{i+tg}=y_i$）。方案数即为 $[k^{n/g}(V-k)^{m/g}+k^{m/g}(V-k)^{n/g}]^g$。

总时间复杂度 $O((n+m)\log V)$。

ARC133F Random Transition (???)

Sol1：

设题目给出的概率为 $w_a$。

大力 DP，用矩阵快速幂优化，可以得到 $O(n^3 \log k)$ 的优秀做法。（特征多项式貌似求得出来，但是转移矩阵不会快速算 $t$ 次幂，做不动）

问题模型看起来很自然，考虑转化一下。假设求由 $a$ 到 $b$ 的概率，问题等价于：

有 $n$ 枚硬币，其中 $a$ 枚硬币朝上。$k$ 次操作，每次随机翻动一枚硬币，求最后有 $b$ 枚硬币朝上的概率。

这样硬币间独立开了。考虑对每枚硬币写出二元生成函数，$x$ 表示翻动次数，$y$ 表示贡献。

$$F(x,y)=\sum\limits_{2 \mid i} \dfrac{x^i}{i!} y+\sum\limits_{2 \nmid i} \dfrac{x^i}{i!}=\dfrac{1}{2}[e^x(y+1)+e^{-x}(y-1)]$$

$$G(x,y)=\sum\limits_{2 \mid i} \dfrac{x^i}{i!}+\sum\limits_{2 \nmid i} \dfrac{x^i}{i!} y=\dfrac{1}{2}[e^x(y+1)-e^{-x}(y-1)]$$

设 $P=e^x(y+1)$，$Q=e^{-x}(y-1)$，则要求的概率即为：

$$\dfrac{1}{k!} \dfrac{1}{n^k} [x^ky^b]F^aG^{n-a}=\dfrac{1}{k!} \dfrac{1}{n^k} \dfrac{1}{2^n} [x^ky^b] (P+Q)^a (P-Q)^{n-a}$$

把括号展开，并对所有 $a$ 求和，设 $\sum\limits_a w_a (P+Q)^a(P-Q)^{n-a}=\sum\limits_{t=0}^n c_t P^t Q^{n-t}$，至于 $c_t$ 怎么求一会再说。

考虑 $[x^k]P^tQ^{n-t}=\dfrac{(2t-n)^k}{k!} (y+1)^t (y-1)^{n-t}$，故答案即为：

$$ANS(y)=\dfrac{1}{n^k} \dfrac{1}{2^n} \sum\limits_t (2t-n)^k c_t (y+1)^t (y-1)^{n-t}$$

惊讶地发现答案的形式与 $c_t$ 的式子是一样的！直接分治乘即可（注意 $t=0$ 要分开算）。

总时间复杂度 $O(n \log^2 n)$。

Sol1+：

注意到时间复杂度瓶颈在于计算：

$$\sum\limits_{i=0}^n w_i (x+1)^i (x-1)^{n-i}$$

$$\begin{aligned} F(x)&=\sum\limits_{i=0}^n w_i (x+1)^i (x-1)^{n-i}\\ &=(x-1)^n \sum\limits_{i=0}^n w_i (\dfrac{x+1}{x-1})^i\\ &=(x-1)^n \sum\limits_{i=0}^n w_i (1+\dfrac{2}{x-1})^i\\ \end{aligned}$$

对 $W(x)$ 先复合 $1+x$，再复合 $\dfrac{-2}{1-x}$ 即可。

时间复杂度 $O(n \log n)$。

ABC238Ex Removing People (3200)

首先可以考虑对每段位置统计次数，然而很难处理。

删除很难搞，时间倒流变成加人。加入一个人 $u$ 时令他面向一个方向，则该方向的邻居 $v$ 需要在原序列中面向 $u$。

考虑区间 DP，设 $f_{l,r}$ 与 $g_{l,r}$ 分别表示 $l$ 位置和 $r$ 位置已经放好人，放 $l \sim r$ 间人的方案数及距离和。

记 $c1=[S_l=R]+[S_r=L]$，$c2_i=[S_l=R](i-l)+[S_r=L](r-i)$，则转移：

$$f_{l,r}=\sum\limits_{i \in (l,r)} \dbinom{r-l-2}{i-l-1} c1 f_{l,i}f_{i,r}$$

$$g_{l,r}=\sum\limits_{i \in (l,r)} \dbinom{r-l-2}{i-l-1} [c2_i f_{l,i}f_{i,r}+c1 f_{l,i}g_{i,r}+c1 g_{l,i}f_{i,r}]$$

时间复杂度 $O(n^3)$。

ARC135E Sequence of Multiples (3200)

看起来很不可做（单调递增且无规律），但发现 $i \mid A_i$，不妨从商下手。

记 $B_i=\dfrac{A_i}{i}$，则有 $B_{i+1}=\lfloor \dfrac{iB_i}{i+1} \rfloor +1=B_i+1-\lceil \dfrac{B_i}{i+1} \rceil$。

故有 $B_i-B_{i+1}=\lceil \dfrac{B_i}{i+1} \rceil-1$，当 $B_i \leq i+1$ 时值就不会再变了。

显然 $\{B_i\}$ 单调不增。考虑其上界，由于 $A_i \leq X+2+3+\cdots+i<X+\dfrac{i(i+1)}{2}$，故 $B_i < \dfrac{X}{i}+i$。

由均值不等式知 $B_{2\sqrt{X}} \leq B_{\sqrt{X}}<2 \sqrt{X}$，故有 $O(\sqrt{X})$ 的做法。

进一步优化，考虑按 $B_i-B_{i+1}$ 分段。下面证明这样段数不超过 $O(X^{1/3})$：

• 设 $n=\lceil X^{1/3} \rceil$，则 $n$ 前至多 $n$ 段；又 $B_n-B_{n+1} \leq n$，$n$ 后至多 $n$ 段。故总段数不超过 $O(X^{1/3})$。

具体实现，假设段首为 $l$，设 $x=\lceil \dfrac{B_i}{i+1} \rceil$，则对于 $r$ 有 $x=\lceil \dfrac{B_l-(r-l)(x-1)}{r+1} \rceil$，解得 $r=\lfloor \dfrac{B_l+lx-x+1}{2x-1} \rfloor$。

总时间复杂度 $O(X^{1/3})$。

ARC136F Flip Cells (3600)

和 ARC133F 联动

停时定理设势函数的做法做不了，因为值域有限，方程无解。

其实对于算停时的题还有另一种做法（参见 【UER #6】逃跑）。设出三个概率型生成函数：

• $F(x)$：$f_t$ 表示由初始状态开始，操作 $t$ 次以后正好是第一次到达目标状态的概率。（答案即为 $F'(1)$）

• $G(x)$：$g_t$ 表示由初始状态开始，操作 $t$ 次以后到达目标状态的概率。

• $H(x)$：$h_t$ 表示由目标状态开始，操作 $t$ 次以后到达目标状态的概率。

由定义，有 $F(x)=G(x)H(x)$。只需要求出 $G(x)$ 及 $H(x)$ 即可得到 $F(x)$。

以 $G(x)$ 为例。发现这个问题跟 ARC133F 几乎一模一样很相似，同样对每个格子设出其翻转偶数次及奇数次的指数型生成函数：

$$\hat P(x)=\sum\limits_{2 \mid i} \dfrac{(x/nm)^i}{i!} = \dfrac{e^{x/nm}+e^{-x/nm}}{2}$$

$$\hat Q(x)=\sum\limits_{2 \nmid i} \dfrac{(x/nm)^i}{i!} = \dfrac{e^{x/nm}-e^{-x/nm}}{2}$$

对于确定的初末状态（指每个格子都已确定），直接将所有对应的生成函数卷起来即可。

然而我们现在只有初始状态，末状态可能有很多种（因为只给定了每行黑格的个数而不是具体方案）。直接对每一行 DP 求出每个指数对应的方案数，再把每一行暴力卷起来得到最终每个指数对应的方案数。（DP 复杂度为 $O(nm^3)$，卷起来复杂度为 $O(n^2m^2)$）

处理完后，只需要把 $\sum\limits_{i=-nm}^{nm} c_i \hat P^{i/nm} \hat Q^{1-i/nm}$ 展开即可。这里与 ARC133F 完全一样，直接背包 $O(n^2m^2)$，分治乘可以优化到 $O(nm \log nm)$。

最后需要计算答案。上面计算的是 $\hat F(x)$ 的指数型生成函数，将所有 $e^{ax}$ 改为 $\dfrac{1}{1-ax}$ 即可转为普通幂级数。

考虑到 $H'(x)=\Big( \dfrac{F(x)}{G(x)} \Big)'=\dfrac{F'(x)G(x)-F(x)G'(x)}{G(x)^2}$，需要求出 $F(1)$ 及 $F'(1)$。

然而 $F(x)$ 中含有 $\dfrac{1}{1-x}$ 项，直接将 $x=1$ 带入 $F'(x)$ 中会出问题。

将 $F(x)$ 及 $G(x)$ 同时乘上 $(1-x)$。则只有 $(1-x)/(1-x)$ 项对 $F(1)$ 有贡献，而 $F'(1)$ 的贡献可以这样求：

$$\left. \dfrac{d}{dx} \Big(\dfrac{1-x}{1-ax}\Big) \right |_{x=1}=\dfrac{1}{a-1}$$

总时间复杂度 $O(n^3m+n^2m^2)$。

ABC241Ex Card Deck Score (2900)

大力写出生成函数：

$$ANS=[x^m]\prod\limits_{i=1}^n \sum\limits_{j=0}^{B_i} (A_ix)^j=[x^m]\prod\limits_{i=1}^n \dfrac{1-(A_ix)^{B_i+1}}{1-A_ix}$$

$m$ 特别大，但是 $n$ 很小，分子可以暴力拆开，然而分母难以处理。

用部分分式分解，设 $\prod\limits_{i=1}^n \dfrac{1}{1-A_ix}=\sum\limits_{i=1}^n c_i \dfrac{1}{1-A_ix}$。解出后即可枚举每一项计算答案。

考虑如何计算 $c_i$。暴力展开两边：

$$1=\sum\limits_{i=1}^n c_i \prod\limits_{j \neq i} (1-A_jx)$$

带入 $x=A_i^{-1}$，则有：

$$1=c_i \prod\limits_{j \neq i} (1-A_jA_i^{-1})$$

可以 $O(n^2)$ 解出。

总时间复杂度 $O(n^2+n2^n)$。

ABC231G Balls in Boxes (2600)

设操作后第 $i$ 个球增加了 $c_i$。则乘积为：

$$\prod\limits_{i=1}^n (A_i+c_i)=\sum\limits_{S \in [n]} (\prod\limits_{t \in S} A_t) (\prod\limits_{t \in [n] \setminus S} c_t)=\sum\limits_{m=0}^n p_mq_{n-m}$$

其中 $p_m$ 为任选 $m$ 个 $A_t$ 的乘积，可以用背包或者分治乘算出。

接下来只需要算 $q_m$，即任选 $m$ 个随机变量 $c_t$ 的乘积的期望。

不妨设这 $m$ 个随机变量就是前 $m$ 个随机变量（其余情况期望相同）。

---

Sol 1

设 $f_{t,i}$ 表示第 $t$ 次是否选择第 $i$ 个球，可以画出 $k \times n$ 的表。

等价于将前 $m$ 个随机变量的和乘起来。将括号拆开，等价于选出有顺序的 $m$ 行 $j_1,\cdots,j_n$，并对 $\prod\limits_{t=1}^m f_{t,j_t}$ 求和。

这个东西是容易的。因为若 $j_t$ 中有相同的数，则一定为 $0$（因为一次只能选一个数）；其它情况下则为 $\dfrac{1}{n^m}$。

故 $q_m=\dfrac{k^{\underline{m}}}{n^m}$。

Sol 2

设出 $m$ 元生成函数，则答案即为 $\Big(\dfrac{\partial^m}{\partial x_1 \cdots \partial x_m} (x_1+x_2+\cdots+x_m)^k\Big) (1,1,\cdots,1)$。

常数扔出来，设 $G=(x_1+x_2+\cdots+x_m)$，考虑偏导：

$$\begin{aligned} \dfrac{\partial^m}{\partial x_1 \cdots \partial x_m} G^k &=k \dfrac{\partial^m}{\partial x_2 \cdots \partial x_m} G^{k-1}\\ &=k(k-1) \dfrac{\partial^m}{\partial x_3 \cdots \partial x_m} G^{k-2}\\ &=\cdots\\ &=k^{\underline{m}} \end{aligned}$$

故答案为 $q_m=\dfrac{k^{\underline{m}}}{n^m}$。

---

总时间复杂度 $O(n^2)$ 或 $O(n \log^2 n)$。

ARC101F Robots and Exits (2900)

假设每个机器人在二维平面内，每一步操作是向上或向右上移动一步，转化为一张 DAG。路径不交，用 LGV 引理解决。

然而终点 $y_1,\cdots,y_k$ 没有确定而且无法枚举。考虑类似扫描线的 DP，一个个确定 $y_i$，再计算下列行列式的和：

$$\begin{vmatrix} \dbinom{n}{y_1-x_1} & \dbinom{n}{y_2-x_1} & \cdots & \dbinom{n}{y_k-x_1}\\ \dbinom{n}{y_1-x_2} & \dbinom{n}{y_2-x_2} & \cdots & \dbinom{n}{y_k-x_2}\\ \vdots & \vdots & \ddots & \vdots\\ \dbinom{n}{y_1-x_k} & \dbinom{n}{y_2-x_k} & \cdots & \dbinom{n}{y_k-x_k}\\ \end{vmatrix}$$

转移时需要枚举最后一列拆开，需要对所有 $\{x_1,\cdots,x_k\}$ 的子集求答案才能转移。故设状态为：

$$f_{S,t}=\sum\limits_{y_1<y_2<\cdots<y_{|S|} \leq t} det \Big( \dbinom{n}{y_j-x_{s_i}} \Big)_{i,j}$$

其中 $s_i$ 为 $S$ 中第 $i$ 大的元素。

转移时，分 $y_{|S|}$ 是否为 $t$ 转移：

$$f_{S,t}=f_{S,t-1}+\sum\limits_{i=1}^{|S|} (-1)^{|S|-i} \dbinom{n}{y_{|S|}-x_{s_i}} f_{S \setminus \{s_i\},t-1}$$

边界情况为 $f_{S,- \infty}=[S= \emptyset]$。

总时间复杂度 $O(k 2^k (x_k+n)$。

ABC242Ex Random Painting (2800)

设一个状态为集合 $S \subseteq \{(l_i,r_i) \mid i \in [1,m]\}$，称一个状态合法如果它覆盖了 $[1,n]$。原过程相当于不断转移状态，直到状态合法。

状态转移形成 DAG，用 ZJOI2020 抽卡 的套路，停时期望等于所有非法状态 出现的概率 乘上 离开该状态期望时间 的和。

大小为 $k$ 的集合 走出该状态期望时间 为 $\dfrac{m}{m-k}$。故只需对每个 $k$ 求大小为 $k$ 的合法状态数量 $f_k$。

大力 DP，先将所有区间按字典序排序（先 $l$ 后 $r$），设 $f_{i,j,k}$ 表示考虑前 $i$ 个区间，覆盖了 $[1,j]$ 的所有格子，大小为 $k$ 的状态数量。

直接转移时间复杂度 $O(nm^2)$。

注意到第三维 $k$ 与给出的区间无关。设 $F(x)=\sum\limits_{i=0}^m f_i x^i$，对于常数 C 可以通过同样的 DP 得到 $F(C)$。

$n$ 较大时，需要用动态开点线段树记录第二维 $j$ 优化转移，单次 DP 时间复杂度 $O(m \log n)$。

做 $m+2$ 次 DP 得到 $m+2$ 个点值，插值还原 $\{f_i\}$，时间复杂度 $O(m^2 \log n)$。

ARC124F Chance Meeting (3200)

为了方便，设 $n=H-1$，$m=W-1$。

容易发现 Camel 向下走与 Cat 向上走对于两人(?)的相对位置而言是等价的。将其视为同一个操作，最后乘上 $\dbinom{2n}{n}$ 即可。于是问题变为了：

从 $(0,0)$ 出发，每次可以向上/左/右走一步，向上走 $2n$ 步，向左与右各走 $m$ 步后到达 $(0,2n)$。求在过程中恰好经过 $(0,n)$ 一次的方案数。

重点是恰好的限制，考虑容斥。

设 $f_i$ 表示向上走 $n$ 步，向左/右各走 $i$ 步后第一次到达 $(0,n)$ 的方案数，$g_i$ 表示向上走 $n$ 步，向左/右各走 $i$ 步后到达 $(0,n)$ 的方案数。显然 $g_i=\dbinom{n+2i}{n,i,i}$。

答案即为 $\dbinom{2n}{n} \sum\limits_{i=0}^m f_i f_{m-i}$。

Sol1(官方题解)：

考虑用 $g_i$ 减去不合法方案得到 $f_i$。枚举上一次经过 $(0,n)$ 是在 $g_j$，要求这 $2(i-j)$ 步都不能经过 $(0,n)$，也就是卡特兰数 $C_{i-j-1}$。

$$f_i=g_i-\sum\limits_{j=0}^{i-1} g_j C_{i-j-1}$$

可以卷积处理，时间复杂度 $O(n \log n)$。

Sol2：

经典套路，再设 $h_i$ 表示从 $(0,n)$ 向左/右各走 $i$ 步回到 $(0,n)$ 的方案数，有 $h_i=\dbinom{2i}{i}$，$H(x)=(1-4x)^{-1/2}$（见 (搜索 取一半组合数)）。

显然 $G=FH$，于是：

$$F^2=\dfrac{G^2}{H^2}=(1-4x)G^2$$

由于只算第 $m$ 项，可以直接拆开计算。

时间复杂度 $O(n)$。

Sol3：(搜索 ARC124F)

ABC245Ex Product Modulo 2 (3000)

将 $M$ 分解质因数 $M=p_1^{e_1} p_2^{e_2} \cdots$，显然每种质因数独立，故只需对 $m=p^e$，$n=N \bmod p^e$ 求原问题答案，再乘起来即可。

设 $n=x p^d (p \nmid x)$。

先考虑 $x \neq 0$ 的情况。钦定序列中恰好有 $d$ 个 $p$，这里的方案数为 $\dbinom{k+d-1}{d}$。在该条件下，得到的 $n$ 的集合为 $S=\{sp^d \mid (s,p^{e-d})=1\}$，又由欧拉定理 $a^{\varphi(p)} \equiv a \pmod p((a,p)=1)$，得到每个 $n$ 的概率都是一样的，算出总方案再除掉 $|S|$ 即可。

设 $c_i$ 表示 $A_i$ 中 $p$ 的次数，则 $p$ 以外的数的选择方案数为：

$$\prod\limits_{i=1}^k p^{e-c_i-1} (p-1)=p^{ke-k-d} (p-1)^k$$

故得到 $n=x p^d$ 的方案数为：

$$\dbinom{k+d-1}{d}\dfrac{p^{ke-k-d} (p-1)^k}{p^{e-d-1}(p-1)}=\dbinom{k+d-1}{d}p^{(k-1)(e-1)}(p-1)^{k-1}$$

对于 $x=0$ 的情况，说明 $p$ 的次数大于等于 $k$。考虑容斥，用全部方案数减去不合法方案数，即：

$$p^{ek}-\sum\limits_{d=0}^{e-1} \dbinom{k+d-1}{d} p^{ke-k-d} (p-1)^k$$

瓶颈在于分解质因数，此处时间复杂度 $O(\sqrt m)$。

ARC126E Infinite Operations (2800)

不知道为什么发现答案即为 $f(A_1,A_2,\cdots,A_n)=\dfrac{1}{2} \sum\limits_{1 \leq i<j \leq n} |A_i-A_j|$，可以简单对方差归纳证明：

• 不妨设 $A_1<A_2<\cdots<A_n$。若 $A_1=A_n$ 则答案为 $0$，显然成立。否则选择 $t \in [1,n)$ 使得 $A_t<A_{t+1}$。

• 将 $A_t$ 与 $A_{t+1}$ 变为 $(A_t+A_{t+1})/2$，方差严格变小。由归纳假设这样构造得到的贡献为（$f$ 只是记号，简写式子）：

$$f(A_1,\cdots,\dfrac{A_t+A_{t+1}}{2},\dfrac{A_t+A_{t+1}}{2},\cdots,A_n)+\dfrac{A_{t+1}-A_t}{2}=f(A_1,A_2,\cdots,A_n)$$

（即合并 $t$ 和 $t+1$ 对 $t$ 与 $t+1$ 以外的点没有影响，只少了 $(A_{t+1}-A_t)/2$ 的贡献）

于是用动态开点线段树维护即可。

时间复杂度 $O((n+q) \log A_i)$。

ARC126F Affine Sort (3500)

考虑 $c \leq k$ 的限制有点奇怪，记 $g(k)$ 表示 $c=k$ 时的合法 $(a,b,c)$ 对数，则 $f(k)=\sum\limits_{i=1}^k g(i)$。

可以证明 $\dfrac{g(k)}{k^2}$ 当 $k \rightarrow +\infty$ 时存在极限，设其为 $c$。则 $g(k) \rightarrow ck^2$，$f(k) \rightarrow \dfrac{1}{3}ck^3$，有 $\lim\limits_{k \rightarrow +\infty} \dfrac{f(k)}{k^3}=\dfrac{1}{3}c$。

问题简化为了求 $\lim\limits_{k \rightarrow +\infty} \dfrac{g(k)}{k^2}$。限制要求 $(aX_i+b) \bmod k$ 单增，不妨转化为 $\dfrac{(aX_i+b) \bmod k}{k}$ 单增。而当 $k$ 足够大时该问题近似是连续的，故可以直接视其为 $\{\dfrac{aX_i+b}{k}\}=\{\alpha X_i+\beta\}$。需要对满足条件的 $(\alpha,\beta)(\alpha,\beta \in [0,1))$ 求二元积分。

为方便设 $X_{0}=X_n$。先不考虑 $\beta$，假设对于某一 $\alpha$，将 $\{\alpha X_i\}$ 画在一个长为 $1$ 的圆周（每个点代表 $[0,1)$ 的数，顺时针增大）上，则必要条件是画出的点依次顺时针排列（即 $P_i$ 的前驱为 $P_{i-1}$，后继为 $P_{i+1}$）。

换句话说，设 $f(\alpha)=\sum\limits_{i=1}^n \{\alpha(X_i-X_{i-1})\}$，则 $\alpha$ 合法的充要条件为 $f(\alpha)=1$（即从头到尾只能转一圈）。

再考虑对于一个合法的 $\alpha$，$\beta$ 需要满足 $\beta+\{\alpha X_1\} \geq 1$，$\beta+\{\alpha X_n\}<1$，故其区间长度为 $\{\alpha(X_1-X_n)\}$。

具体而言，枚举每个 $i$，$\{\alpha(X_i-X_{i-1})\}$ 是一个分段函数，形如 $\{\alpha(X_i-X_{i-1})\}=\alpha(X_i-X_{i-1})+d_t(\alpha \in [l_t,r_t])$，而段数只有约 $O(|X_i-X_{i-1}|)$ 个。

又所有斜率加起来为 $\sum\limits_{i=1}^n (X_i-X_{i-1})=0$，故 $f(\alpha)$ 也是一个分段函数，且每一段都为常数，而段数为大约 $S=\sum\limits_{i=1}^n |X_i-X_{i-1}|$。枚举每一段，$\beta$ 的合法区间长度形如一次函数，对 $\beta$ 积分即可。

时间复杂度 $O(S \log S)$。

ARC128F Game against Robot (3800)

不看题解做出银牌题，可喜可贺

下面设 $n=N/2$。

先考虑如何判断给定排列 $p$ 的答案。显然直接贪心吃最大是错的，因为 $B$ 的策略是固定（而不是最优）的，$A$ 选较小值可能可以使 $B$ 选较小值从而增大 $A$ 的收益。

将 $a$ 中的数按 $p$ 排列成一排，则 $B$ 会优先烧最靠前的数。先不考虑每个数的权值，来考虑 $A$ 最后能吃到哪些数。

• 其中一个答案是：设 $s_i$ 表示 前 $i$ 个数中 Snuke 吃掉的数量，则其合法当且仅当 $\forall i,s_i \leq i-s_i+1$。然而这个性质难以计算答案。

• 换一种想法，设 $A$ 最后吃的数为 $1 \leq b_1<b_2<\cdots<b_n \leq 2n$，则其合法的充要条件为 $\forall i,b_i \geq 2i-1$。利用这个性质，从后往前维护优先队列，每次加入序列末尾两个数并删掉优先队列的最大数，操作 $n$ 次后所有删掉的数的和即为答案。

由于是枚举所有排列，具有对称性，因此可以将整个序列翻转，改为从前往后维护优先队列。

考虑原问题。由上面过程可以看到 $A$ 的策略与 $a_i$ 的具体值无关，只与大小关系有关。先将 $a$ 从大到小排序，求出第 $i$ 大数在所有情况中被选中的次数 $f_i$，则答案即为 $\sum\limits_{i=1}^{2n} a_if_i$。

---

恰好不好求，改为求 $g_m$ 表示前 $m$ 大的数在所有情况中被选中的次数之和。将前 $m$ 大的数染黑，那么对于一个排列 $p$ 只需要考虑选了多少个黑数，下面对黑白序列计算，再乘上 $m!(2n-m)!$ 即可。

设第 $t$ 次向优先队列中加的黑数数量为 $c_t \in [0,2]$ 且 $\sum\limits_{t=1}^{2n} c_t=m$。设 $x$ 为优先队列的大小，则每次 $x \leftarrow \max(0,x+c_t-1)$。

记 $d_t=c_t-1$，看作在网格图上移动：从 $(0,0)$ 出发，每次向右走一步，向上走 $d_t$ 步，若跨越 $x$ 轴就强行贴着 $x$ 轴走（图中的红边）。

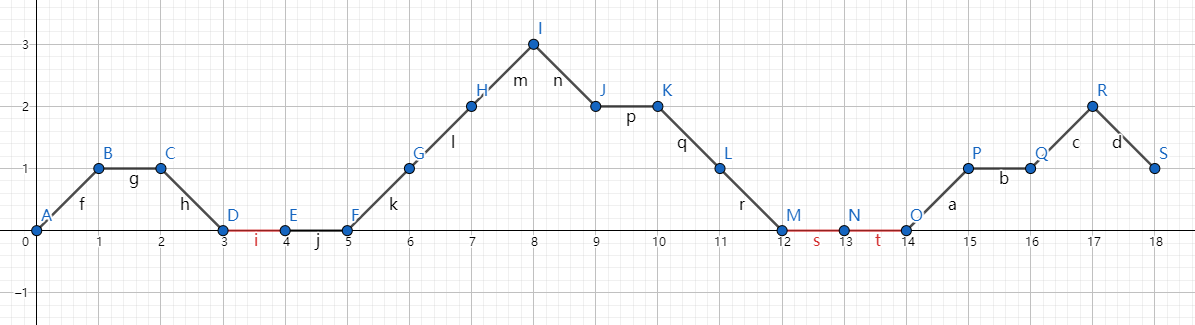
则红边对应着删去白数，数出所有情况中红边的总数，容斥即可得到删去黑数的总数。

强行不跨越 $x$ 轴的操作看起来很奇怪，若允许跨越 $x$ 轴，则最后会走到 $(n,m-n)$：

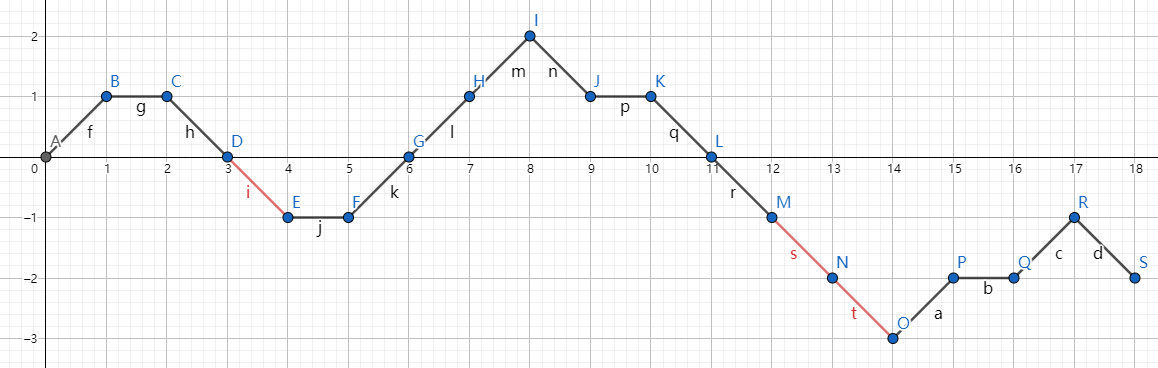
发现红边即对应走到前缀最小值处。而每次前缀最小值只会减少 $1$，故红边的数量是最低点纵坐标的相反数。

---

引理：从 $(0,0)$ 走到 $(n,m)$，每次可以向右上/右/右下走，方案数分别为 $1,2,1$。则路径方案数总数为 $\dbinom{2n}{n+m}$。

证明：

$$\begin{aligned} ANS &=[x^m](x+2+x^{-1})^n\\ &=[x^m]x^{-n}(x^2+2x+1)^n\\ &=[x^{m+n}](x+1)^{2n}\\ &=\dbinom{2n}{n+m}\\ \end{aligned}$$

设 $p_{m,k},q_{m,k}(k \in [-n,\min(0,m-n)])$ 分别表示最小值 等于 及 大于等于 $k$ 的路径方案数总数。用类似卡特兰数的套路，有：

$$q_{m,k}=\dbinom{2n}{m-n+n}-\dbinom{2n}{2(k-1)-m+n+n}=\dbinom{2n}{m}-\dbinom{2n}{m-2k+2}$$

$$p_{m,k}=q_{m,k+1}-q_{m,k}=\dbinom{2n}{m-2k}-\dbinom{2n}{m-2k+2}$$

设 $-lim=\min(0,n-m),lim=\max(0,m-n)$，有：

$$\begin{aligned} \dfrac{g_m}{m!(2n-m)!}&=\sum\limits_{k=-n}^{-lim} (n+k) \Big[\dbinom{2n}{m-2k}-\dbinom{2n}{m-2k+2} \Big]\\ &=n\sum\limits_{k=-n}^{-lim} \Big[\dbinom{2n}{m-2k}-\dbinom{2n}{m-2k+2} \Big]+\sum\limits_{k=-n}^{-lim} k \Big[\dbinom{2n}{m-2k}-\dbinom{2n}{m-2k+2} \Big]\\ &=n \dbinom{2n}{m+2lim}-\sum\limits_{k=lim}^{n} k \Big[\dbinom{2n}{m+2k}-\dbinom{2n}{m+2k+2} \Big]\\ &=n \dbinom{2n}{m+2lim}-\sum\limits_{k=lim} k \dbinom{2n}{m+2k}+\sum\limits_{k=lim} k \dbinom{2n}{m+2k+2}\\ &=n \dbinom{2n}{m+2lim}-\sum\limits_{k=lim} k \dbinom{2n}{m+2k}+\sum\limits_{k=lim+1} (k-1) \dbinom{2n}{m+2k}\\ &=n \dbinom{2n}{m+2lim}-lim \dbinom{2n}{m+2lim}-\sum\limits_{k=lim+1}^n \dbinom{2n}{m+2k}\\ \end{aligned}$$

预处理即可 $O(1)$ 计算，该部分复杂度 $O(n)$。

总时间复杂度 $O(n+\text{sort})$。

ARC115E LEQ and NEQ (2400)

对条件容斥，于是就变成了划分问题。

注意到一段的权值只与最小值有关，于是建出笛卡尔树类似 CDQ 分治 DP 即可。

使用差分及前缀和优化即可做到 $O(n)$。

ARC112E Cigar Box (2700)

考虑操作对序列的影响是怎样的。显然最后的状态只与 每个数最后一次操作被放在哪一边有关，故对每个数考虑其最后一次操作，称其为关键操作。

设共 $L$ 个数最后被操作到左边，$R$ 个数最后被操作到右边，显然这 $L$ 个数必须是 $a_1,a_2,\cdots,a_L$（并且它们对应关键操作的时间必须单增），这 $R$ 个数必须是 $a_{n-R+1},a_{n-R+2},\cdots,a_n$（并且它们对应关键操作的时间必须单减），而中间 $a_{L+1},a_{L+2},\cdots,a_{n-R}$ 必须单调递增。

于是，倒序考虑每个操作，只需要确定以下信息，就可以唯一对应到一种操作序列：

• 关键操作是哪些，它们的方向分别是哪里。
• 对于每个非关键操作，其操作的是哪个数（该数必须已经被关键操作过了）。

考虑 DP，设 $f_{i,L,R}$ 表示确定了 $i$ 个操作，其中有 $L$ 个向左的关键操作，$R$ 个向右的关键操作的方案数。

$$f_{i+1,L+1,R} \leftarrow f_{i,L,R}, \, f_{i+1,L,R+1} \leftarrow f_{i,L,R}$$

$$f_{i+1,L,R} \leftarrow 2(L+R) f_{i,L,R}$$

注意到系数只与 $L+R$ 有关，即只关心总关键操作个数。故将状态改为总关键操作个数，设 $f_{i,L,R}=g_{i,L+R}\dbinom{L+R}{L}$，同样转移即可。

最后将对所有满足 $a_l<a_{l+1}<\cdots<a_r$ 的 $f_{i,l-1,n-r}$ 求和即可。

时间复杂度 $O(nm)$。

ARC124E Pass to Next (3000)

设第 $i$ 个人给出了 $b_i$ 个球，则传球后第 $i$ 个人有 $a_i-b_i+b_{i-1}$ 个球。

注意到传球后的状态与 $b_i-b_{i-1}$ 有关，若 $\min b_i>0$，将所有 $b_i$ 减去 $1$ 后状态不变；另一方面，若 $\min b_i=0$，则其对应的状态是唯一的。故用总方案减去限制 $\forall i,b_i>0$ 的方案数即为答案。

以总方案为例，所求即为：

$$\sum\limits_{\{b_i\},b_i \leq a_i} \prod\limits_{i=1}^n (b_{i-1}+a_i-b_i)$$

考虑拆括号。每个位置只会被覆盖 $0/1/2$ 次，这取决于两端括号的选择。

用 DP 描述括号的选择。先断环为链，确定 $(b_n+a_1-b_1)$ 的选择。设 $f_{i,id}$ 表示前 $i$ 个括号（即统计到 $(b_{i-1}+a_i-b_i)$），第 $i$ 个括号选择哪边（$id=0$ 为左边 $b_{i-1}$，否则为右边 $a_i-b_i$），所有选择方案对应的和。其中若 $id=0$ 则计算该括号的贡献，否则不计算。

$$f_{i+1,0} \leftarrow \Big(\sum\limits_{b_i=0}^{a_i} b_i \Big) f_{i,0}$$

$$f_{i+1,1} \leftarrow \Big(\sum\limits_{b_i=0}^{a_i} 1 \Big) a_i f_{i,0}$$

$$f_{i+1,0} \leftarrow \Big(\sum\limits_{b_i=0}^{a_i} b_i(a_i-b_i) \Big) f_{i,1}$$

$$f_{i+1,1} \leftarrow \Big(\sum\limits_{b_i=0}^{a_i} (a_i-b_i) \Big) f_{i,1}$$

统计与最初确定的 $(b_n+a_1-b_1)$ 选择符合的状态求和即可得到答案。

总时间复杂度 $O(n)$。

ARC131F ARC Stamp (3500)

考虑给定某个初状态如何判断合法。考虑倒推，每次将一个 ARC 变成 ???，表示该位可以任意填。

容易发现每次可以将 $6$ 种子区间变成 ???：ARC，?RC，??C，AR?，A??，?R?。（A?C 不会在过程中出现）

将给出的 $T$ 分解成 ARC，RC，C，AR，A，R，于是每次占领一定是占领某一段。

考虑 DP，可以设 $f_{i,j,id}$ 表示考虑前 $i$ 段，最少操作次数为 $j$，是否选第 $i$ 段的方案数。然而直接转移会算重，例如 [ARC][RC] 中，对于 $S$ 为 ARCRC 及 ARCAA 两种情况，在考虑 [ARC] 时并不知道 [RC] 是否要占领，于是也不知道是否要统计步数。

设 $f_{i,j,id}$ 表示考虑前 $i$ 段，最少操作次数为 $j$，第 $i$ 段与第 $i+1$ 段是否都占领的方案数。

在转移时，需要考虑该转移是否是必要的。

这里以 [ARC] 的转移为例：

• $f_{i,j,0} \leftarrow f_{i-1,j,0}$，不占领。

• $f_{i,j+1,1} \leftarrow 27f_{i-1,j,0}$，占领，且这步必要（前一步依赖）。

• $f_{i,j+1,0} \leftarrow 27f_{i-1,j,1}$，占领，且这步必要（后一步依赖）。

• $f_{i,j+1,1} \leftarrow 27f_{i-1,j,1}$，占领，且这步必要（前后一步依赖）。

• $f_{i,j+1,0} \leftarrow 26f_{i-1,j,0}$，只占领 $i$ 而不占领前后，这步不必要。

注意上述转移在两个 [ARC] 间会算重（因为 [ARC] 不需要依赖前后），手动在 [ARC] 间加入间隔符 [X] 即可。

总时间复杂度 $O(|T|k)$。

ARC138E Decreasing Subsequence (3600)

妙妙双射题？

考虑一张 $n+1$ 个点的有向图，对所有 $A_i>0$ 连边 $(i,A_i-1)$。

显然这张图只能由大连向小，由若干条链构成。长度为 $k$ 的下降子序列对应着关键边 $(R_1,L_1),\cdots,(R_k,L_k)(L_1 \leq \cdots \leq L_k \leq R_k \leq \cdots \leq R_1)$，且这些边都在不同的链里。

将 $k$ 条关键边所在的链拎出来，并用每条关键边将其所在的链割成两半。设所有在 $L_i$ 一侧的点集为 $A$，所有在 $R_i$ 一侧的点集为 $B$，显然 $\max \{A\}<\min \{B\}$。

注意到：对于每个 $\max \{A\}<\min \{B\}$ 的 $(A,B)$ 及将 $A$，$B$ 各连成 $k$ 条链的方案，有且仅有唯一的连关键边方式 $(R_1,L_1),\cdots,(R_k,L_k)$ 使得 $L_1 \leq \cdots \leq L_k \leq R_k \leq \cdots \leq R_1$。

于是只需要预处理 $f_{i,j}$ 表示将 $i+1$ 个点连成 $j$ 条链的方案数。枚举 $|A|=x$，$|B|=y$，则选择 $(A,B)$ 的方案数为 $\dbinom{n+1}{x+y}$，即可快速计算。

时间复杂度 $O(n^2)$。

ARC107D Number of Multisets (2100)

设 $f_{i,j}$ 表示用 $i$ 个数凑出 $j$ 的方案数。

考虑转移，要么去掉一个 $1$（如果当前状态有 $1$），要么全部乘 $2$（如果当前状态没有 $1$），即：

$$f_{i,j}=f_{i-1,j-1}+f_{i,2j}$$

时间复杂度 $O(n^2)$。

ARC116D I Wanna Win The Game (1700)

设 $f_{i}$ 表示 $n$ 个数和为 $i$，异或和为 $0$ 的方案数。显然 $i$ 必须为奇数。

考虑枚举所有数的最后一位有 $j$ 个是 $1$：

$$f_{i}=\sum\limits_{2 \mid j,j \in [0,n]} \dbinom{n}{j} f_{(i-j)/2}$$

时间复杂度 $O(n^2)$。

AGC022F Checkers (3600)

神仙题

• $O(n^5)$

由于 $X$ 太大，可以把 $X^k$ 视作基底，每个数看作 $n$ 维空间内的点。

对 $u,v$ 的一次操作认为是新建一个点 $t$ 连向 $u$ 及 $v$，边权分别为 $2$ 及 $-1$，表示 $t=2u-v$。

最后根到某点的路径权积即为该点贡献。贡献一定形如 $\pm 2^k$，下面计算每维贡献的可重集，最后乘上可重排即可。

考虑从根向下 DP。设 $f_{i,x,y}$ 表示共 $i$ 个点，权值绝对值最大的点（设权为 $\pm 2^k$，不关心 $k$ 到底是多少）中有 $x$ 个为正，$y$ 个为负的方案数。

每次转移枚举 $a$ 个权 $2^k$ 的点分裂，$b$ 个权 $-2^k$ 的点分裂。注意 $\pm 2^k$ 分裂后会产生 $\pm 2^{k+1}$ 及 $\mp 2^k$，还可以继续分裂，故让它们完全分裂（之后不会再分裂）。

容易算出完全分裂后还剩下 $x-a+b$ 个 $2^k$ 及 $y-b+a$ 个 $-2^k$，计入可重排里。故转移：

$$f_{i+a+b,a,b} \leftarrow \dfrac{1}{(x-a+b)!(y-b+a)!} f_{i,x,y}$$

初始状态 $f_{1,1,0}=1$，$Ans=n!f_{n,0,0}$。

时间复杂度 $O(n^5)$，难以优化。但足以通过本题

• $O(n^4)$

上面的做法瓶颈在于需要记录最后一层的正负点个数。

考虑换一种建图方式，将 $-1$ 边缩起来。即对 $u,v$ 操作直接将 $u$ 连向 $v$（$u$ 为 $v$ 的父亲）。注意这里儿子有序。

此时一个点的贡献绝对值为 $2^{dep}$，符号取决于其 儿子个数+祖先左侧儿子个数 的奇偶性。将每个点的符号与其父亲差分即为 其儿子个数+父亲右侧儿子个数+$1$。

下面称有奇数个儿子的点为特殊的。

仍然从上到下对每一层 DP，但由于符号与儿子个数相关需要改变状态。设 $f_{i,j}$ 表示共 $i$ 个点，该层有 $j$ 个特殊点 的方案数。

设下一层有 $k$ 个点，若不考虑这些点中儿子个数对符号的影响，则每个父亲的儿子符号从右到左是 $-1,1,\cdots,-1/1$。故 $1$ 共有 $\dfrac{k-j}{2}$ 个，而 $-1$ 有 $\dfrac{k+j}{2}$。

设考虑这些点中儿子个数的影响后共有 $t$ 个点为 $1$。注意到若有两个特殊点权一正一负，可以令它们儿子个数变为偶数，不会影响权值。故令每一种方案唯一对应到 特殊点数量最少（即 $|t-(k-j)/2|$ 个）的方案，不会算重。有转移：

$$f_{i+k,|t-(k-j)/2|} \leftarrow \dfrac{1}{t!(k-t)!} f_{i,j}$$

初始状态 $f_{1,0}=f_{1,1}=1$，$Ans=n!f_{n,0}$。

时间复杂度 $O(n^4)$。

• $O(n^3)$

先将上述转移式改写一下，令 $x=t$，$y=k-t$，则：

$$f_{i+x+y,|(x-y-j)/2|} \leftarrow \dfrac{1}{x!y!} f_{i,j}$$

注意到 $(i+x,x-j)$ 相同时转移只与 $y$ 有关。故分步转移：

$$g_{i+x,x-j} \leftarrow \dfrac{1}{x!} f_{i,j}$$

$$f_{i+x+y,|(x-y-j)/2|} \leftarrow \dfrac{1}{y!} g_{i+x,x-j}$$

$$f_{A,|(B-y)/2|} \leftarrow \dfrac{1}{y!} g_{A,B}$$

注意转移条件 $x+y \geq \max(1,j)$，$2 \mid x+y+j$。

时间复杂度 $O(n^3)$。

ARC139D Priority Queue 2 (2800)

先把第 $x$ 小改为第 $n+1-x+1$ 大（即删除后允许最大 $n-x+1$ 个数留下）。

暴力枚举值域，对每个 $t \in [1,m]$ 计算最后 $\geq t$ 的数的期望个数，最后相加即为答案。

设最开始时 $\geq t$ 的数有 $A$ 个，$k$ 步中一共加入了 $B$ 个 $\geq t$ 的数。则：

• 若 $A \leq n-x+1$，则每次操作后 $\geq t$ 的数始终不超过 $n-x+1$ 个，故最后 $\geq t$ 的数有 $\min(A+B,n-x+1)$ 个。

• 若 $A > n-x+1$，则每次操作后 $\geq t$ 的数至少有 $n-x+1$ 个，故最后 $\geq t$ 的数有 $\max(A+B-k,n-x+1)$ 个。

暴力枚举 $p$，乘上方案数即可。

预处理组合数及幂次可做到 $O(n+mk)$。

ARC139E Wazir (3200)

当 $n,m$ 均为偶数时，显然最优方案为黑白间隔染色，方案数为 $2$。

否则，可以选择交换 $n$，$m$ 使得其二之一成立：

• $n$ 为偶数，$m$ 为奇数。

• $n,m$ 均为奇数且 $n \geq m$。

当 $m$ 为奇数时，一行中最多能填 $\dfrac{m-1}{2}$ 个，且此时有且仅有两个相邻的空位。

设第 $i$ 行的空位位置为 $p_i$，注意到：

第 $i$ 行与第 $i+1$ 行满足要求当且仅当 $p_{i+1}=p_i \pm 1 \pmod m$。

于是可以说明最优方案的黑格数为 $\lfloor \dfrac{n}{2} \rfloor \dfrac{m-1}{2}$：

• 当 $n$ 为偶数时，令 $\{p_i\}=\{0,1,0,1,\cdots,0,1\}$。

• 当 $n$ 为奇数（$n \geq m$）时，令 $\{p_i\}=\{0,1,0,1,\cdots,1,0,1,2,\cdots\,m-2,m-1\}$。

考虑算方案数。先假设 $p_0=0$，最后再乘上 $m$。即求：

$$\sum\limits_{x+y=n} [m \mid x-y] \dbinom{n}{x}$$

当 $n$ 较小时，暴力计算即可。

当 $m$ 较小时，只需要计算：

$$(x+x^{-1})^n \pmod{x^m-1}$$

使用多项式快速幂及多项式取模即可。

总时间复杂度 $O(\min(n,m) \log n \log m)$。

ARC127E Priority Queue (2700)

记 $n=A$，$m=B$。

考虑判断终态 $s_1,s_2,\cdots,s_{n-m}$ 是否可行。考虑倒推，倒着考虑每个操作：

• 若遇到 $1$ 操作，则从优先队列中删除一个数。

• 若遇到 $2$ 操作，则将一个未被加入过的数加入优先队列，且要求该数比优先队列中所有数都大。

若存在一种操作方式完成所有操作，则终态合法。

不难发现最优策略下 $1$ 操作删除的数一定是最大的，而 $2$ 操作加入的数会按照 $s_{n-m}+1,s_{n-m}+2,\cdots,n,s_{n-m-1}+1,s_{n-m-2}+2,\cdots$ 的顺序加入。

那么预处理出 $p_i$ 表示删掉 $s_{n-m+1-i}$ 时（即第一次 $cnt_1-cnt_2=i$）进行的 $2$ 操作的数量。则 $s_i$ 合法当且仅当 $\forall i,n-s_{n-m+1-i}-i+1 \geq p_i$（即 $s_{n-m+1-i}$ 后面的空位数）。

即问题转化为：

求 $0 \leq a_1 \leq a_2 \leq \cdots \leq a_{n-m} \leq m$ 的数量使得 $\forall i,a_i \geq p_i$。

可以直接 $O(n^2)$ DP，也可参照 gym102978J Japanese Knowledge 用分治乘优化到 $O(n \log^2 n)$。

真 · Japanese Knowledge

ABC249G Xor Cards (2800)

把卡片的 $A_i$ 扔进线性基 $P$ 里（线性基需记录对应的 $B_i$），插不进去的将 $B_i$ 放到另一个线性基 $Q$ 里表示可以随意用。

从高位向低位枚举 $P$ 中元素。记录当前钦定选的 $A_i$ 异或和 $cur$ 及 $B_i$ 异或和 $val$。假设枚举到第 $i$ 位（$cur_i,K_i$ 分别表示 $cur$ 及 $K$ 在二进制下的第 $i$ 位，$P_i$ 表示 $P$ 的第 $i$ 位元素）：

• 若 $cur_i=0,K_i=0$，则必须不选，跳过。

• 若 $cur_i=0,K_i=1$，若 $P_i=0$ 则直接跳过；否则若钦定不选则 后面的位及 $Q$ 可以任意选计入答案，若钦定选择则继续下一位。

• 若 $cur_i=1,K_i=0$，则必须选，若 $P_i=0$ 则退出，否则跳过。

• 若 $cur_i=1,K_i=1$，若 $P_i=0$ 则直接跳过；否则若钦定选则 后面的位及 $Q$ 可以任意选计入答案，若钦定不选则继续下一位。

最后若 $cur=K$ 可以在 $Q$ 中任意选计入答案。

判断无解需要记录目前 是否已经钦定选数 及 线性基里是否有元素。

预处理线性基可做到 $O(n \log W+\log^2 W)$。

所以为什么官方题解和 User Editorial 都是三方的啊

ABC129Ex Dye Color (3500)

算停时，用 势函数和鞅的停时定理！

对每种颜色的出现次数 $a_i$ 设势函数 $\varphi(x)$。设 $p_{i,j}$ 表示一次操作后某种颜色 $X$ 出现次数由 $i$ 变为 $j$ 的概率，则我们希望：

$$1+\sum\limits_{i=1}^n \sum\limits_{j=0}^{a_i+1} p_{a_i,j} \varphi(j)=\sum\limits_{i=1}^n \varphi(a_i)$$

$$\varphi(i)=\sum\limits_{j=0}^{i+1} p_{i,j} \varphi(j)-\dfrac{1}{n}(i<n),\varphi(n)=0$$

考虑计算 $p_{i,j}$。分两种情况：

• 选的颜色中没有颜色 $X$，则概率为：

$$\begin{aligned} S_1 &=\sum\limits_{t=0}^{n-i} \dfrac{1}{2^n} \dbinom{i}{i-j} \dbinom{n-i}{t} \dfrac{\dbinom{n-1}{(i-j+t)}}{\dbinom{n}{(i-j+t)}}\\ &=\dfrac{1}{2^n} \dbinom{i}{j} \sum\limits_{t=0}^{n-i} \dbinom{n-i}{t} \dfrac{n-(i-j+t)}{n}\\ &=\dfrac{1}{2^n} \dbinom{i}{j} \big [ (n-i+j)2^{n-i}-(n-i)2^{n-i-1} \big ]\\ \end{aligned}$$

• 选的颜色中有颜色 $X$。则概率为：

$$\begin{aligned} S_2 &=\sum\limits_{t=0}^{n-i} \dfrac{1}{2^n} \dbinom{i}{i-j+1} \dbinom{n-i}{t} \dfrac{i-j+1+t}{n}\\ &=\dfrac{1}{2^n} \dbinom{i}{j-1} \big [ (i-j+1)2^{n-i}+(n-i)2^{n-i-1} \big ]\\ \end{aligned}$$

于是 $p_{i,j}=S_1+S_2$ 可以 $O(1)$ 算出。

由于是下海森堡矩阵，可以通过倒推 $O(n^2)$ 消元并解出 $\varphi(x)$，计算答案。

总时间复杂度 $O(n^2)$。

ARC140F ABS Permutation (Count ver.) (3400)

先考虑 $M=1$ 的情况。注意到满足条件的位置连起来会将整个数组划分成一条条链，等价于数链的条数，而链是好处理的。

假如钦定了每一条链的位置（未填数），方案数容易计算。难点在于要求两条不同的链不能相接。

上容斥，设 $f_i$ 表示满足条件的位置恰好有 $i$ 个，$g_i$ 表示钦定有 $n-i$ 条链（即有些满足条件的位置可能不被计入），有：

$$g_k=\sum\limits_i \dbinom{i}{k} f_i$$

$$f_k=\sum\limits_i (-1)^{i-k} \dbinom{i}{k} g_i$$

该式直接差卷积即可。下面考虑如何算 $g_k$。

$g_k$ 的意义为：将长为 $n$ 的数组划分为 $k$ 段 $c_1,\cdots,c_k$，其权值为：

$$k! 2^{\sum\limits_{i} [c_i>1]}$$

$g_k$ 即为所有划分方案的权值和。

可参照 CF1553I Stairs，使用分治乘（需要记录两端是否为 $1$），复杂度为 $O(16 n \log^2 n)$。这里由于是上述题目中 $a_i$ 全为 $1$ 的特殊情况，可以改为倍增 FFT，复杂度为 $O(16 n \log n)$。

接下来考虑 $M > 1$。记 $Q=P^{-1}$ 满足 $Q_{P_i}=i$。则 $|P_i-P_{i+1}|=M$ 等价于 $|Q_i-Q_{i+M}|=1$。又注意到位置可以随意互换，故这个模型等价于若干条互相独立的链。对每条链做 $M=1$ 的倍增 NTT 再全部分治乘卷起来即可。

时间复杂度 $O(16n \log n+n \log^2 n)$。

AGC057E RowCol/ColRow Sort (4100)

个人感觉这一场最有意思的题

考虑如何判断一个矩阵是否合法。

由排序网络的 0-1 原理，对于每个 $k$，将不超过 $k$ 的数涂黑，得到 $A_k$ 及 $B_k$。若 $A_k$ 按两种方式排序后都得到 $B_k$，则合法。

记矩阵 $M$ 的每行黑格子数的可重集为 $R_M$，每列黑格子数的可重集为 $C_M$。

引理：对于所有按行或按列排序后的 $n$ 行 $m$ 列矩阵 $M$，$f:{R_M} \rightarrow C_M$ 构成双射。
证明：不妨设 $M$ 按行有序。将所有列按照黑格数量递减排序，显然 $R_M$ 及 $C_M$ 不变，而此时 $M$ 按列也有序，故 $R_M$ 与 $C_M$ 唯一对应。

结论：矩阵 $A$ 合法当且仅当 $R_A=R_B,C_A=C_B$。
证明：将 $A$ 按行排序后得到 $A'$，有 $R_A=R_{A'}$。由于 $A'$ 按列排序后得到 $B$，故 $C_{A'}=C_B$。由引理，$R_{A'}=R_B$，故 $R_A=R_B$。同理 $C_A=C_B$，可证得必要性，而充分性显然。

注意到颜色数很少，不妨按颜色分层。对于每个 $k$，只需要计算出在 $B_{k+1}$ 中填出 $B_k$ 的方案数，全部相乘即可得到答案。即，将 $B_{k+1}$ 按行列排序后得到 $B'_{k+1}$，在黑格中选一些格子，选出的格子组成矩阵的 $M$ 满足 $R_M=R_{B_{k}},C_M=C_{B_{k}}$。

由于引理，$M$ 由且仅由 $B_k$ 交换一些行列得到。不妨设行交换的排列为 $p_1,\cdots,p_n$，列交换的排列为 $q_1,\cdots,q_m$。只需要满足：

$$B_{k_{i,j}}=1 \Rightarrow B'_{k+1_{p_i,q_j}}=1$$

设 $a_i$ 表示 $B_k$ 第 $i$ 行的黑格数，$b_i$ 表示 $B'_{k+1}$ 第 $j$ 列黑格数，则条件等价于：

$$j \leq a_i \Rightarrow p_i \leq b_{q_j}$$

$$\forall i \in [1,n],p_i \leq b_{\max\{q_1,q_2,\cdots,q_{a_i}\}}$$

注意到 $\{a_i\}$ 及 $\{b_i\}$ 均单调不增，考虑按 $x=\max\{q_1,q_2,\cdots,q_{a_i}\}$ 从后向前 DP。

设 $f_{i,j}$ 表示 $\max\{q_1,q_2,\cdots,q_i\}=j$ 的方案数，可以在转移时维护 $\{q_i\}$ 的方案数。再维护一个指针 $t$，容易在 $a_t=i$ 时计算 $\{p_i\}$ 的方案数：

$$f_{i,j} \leftarrow (j-i+1) f_{i-1,j}+\sum\limits_{k<j} f_{i-1,k}$$

$$f_{i,j} \leftarrow (b_j-t+1) f_{i,j}$$

最后由于 $R_k,C_k$ 中重复的数会被计算多次但方案是相同的，所以要除掉可重排。注意 $a_i,b_j=0$ 的要删掉，不然会算重。

前缀和优化可做到 $O(nm+m^2)$。总时间复杂度 $O(B_{i,j}(nm+m^2))$。

ARC118E Avoid Permutations (3100)

从对每个 $P$ 计算 $f(P)$ 的角度来看十分不可做。由于可以从障碍中间穿过，只能用 DP 解决。

换一个角度，对每条路径统计放障碍的方案数。障碍不能碰到路径 的限制比较难办，考虑容斥，钦定一部分障碍必须放在路径上。

一边 DP 一边进行容斥。注意到最后需要根据钦定放障碍的数量来计算其它障碍的方案，并且两行间的交界处会出现两格子同列的情况。故设 $f_{i,j,k,id_1}$ 表示在第 $i$ 行走到第 $j$ 列（下一步直接向下一行走），已经钦定放了 $k$ 个障碍，障碍是否放在 $(i,j)$ 的权值。转移需要枚举下一行走到哪，复杂度 $O(n^4)$。

在每一行转移内部用分步 DP 来优化。将状态改为 $f_{i,j,k,id_1,id_2}$，表示在第 $i$ 行走到第 $j$ 列，已经钦定放了 $k$ 个障碍，该行是否已放障碍，该列是否已放障碍的权值。转移只需考虑相邻的两个格子，复杂度 $O(n^3)$。

AGC053C Random Card Game (2900)

本文中认为每次操作拿走较大（而非较小）的牌，与原题等价。

容易发现被拿空的牌堆是确定的：$1$ 号牌不可能被拿走。

设含有 $1$ 号牌的牌堆为 $A$，另一牌堆为 $B$。

$B$ 中的每张牌 $B_i$ 都会被 $A$ 中的某张牌 $A_j$ 删掉，且满足 $A_j<B_i$。设最小满足此条件的 $j$ 为 $p_i$。

显然下界为 $n+\max \{p_i-i\}$，可以通过以下策略达到：

• 若有 $A_i<B_i$ 就对这样的 $i$ 中最大的 $i$ 删掉 $B_i$（故不会互相影响）；否则就将 $A_1$ 删去（若 $A_1$ 不能删去则说明 $A_1<B_1$，矛盾）。

这样 $B$ 中的每张卡能删就删，删去 $A_1$ 的次数就是 $\max \{p_i-i\}$。

设 $\max \{p_i-i\} \leq k$ 的概率为 $f_k$，则答案为 $2n-\sum\limits_{k=0}^{n-1} 2f_k$（乘 $2$ 是因为 $A,B$ 可互换）。

即计算对所有 $i \in [1,n]$，存在 $j \in [1,\min(i+k,n)]$ 使得 $A_j < B_i$ 的概率。记该事件为 $C_i$，则：

$$\begin{aligned} f_k &= P(C_1 \cap C_2 \cap \cdots \cap C_n)\\ &= P(C_1) P(C_2 | C_1) P(C_3| C_1 \cap C_2) \cdots P(C_n | C_1 \cap \cdots \cap C_{n-1}) \end{aligned}$$

而 $C_i | C_1 \cap \cdots \cap C_{i-1}$ 不成立当且仅当 $B_i$ 是 $A_1,\cdots,A_{\min(i+k,n)},B_1,\cdots,B_i$ 中最小的（若存在 $B_j \leq B_i$，由于 $C_j$ 成立 $C_i$ 也一定成立）。故概率为 $1-\dfrac{1}{i+\min(i+k)}$。

$$f_k=\prod\limits_{i=1}^{n-k} \dfrac{2i+k-1}{2i+k} \prod\limits_{i=n-k+1}^{n} \dfrac{n+i-1}{n+i}$$

预处理后可以 $O(1)$ 计算。总时间复杂度 $O(n)$。

ARC133F Many Xor Optimization Problems (?)

q-analog 普及题

对于每个向量空间，求出其线性基并对主元位消元。

设主元位分别为 $x_1,x_2,\cdots,x_k$，下面分成三部分计算：

• 主元位 $x_1,x_2,\cdots,x_k$ 对应的向量空间数量。

• 主元位为 $x_1,x_2,\cdots,x_k$ 的向量空间的最大子集异或和的期望值。

• 主元位为 $x_1,x_2,\cdots,x_k$ 的基底数量。

第一个问题显然只与 $k$ 有关。只需要数 $k$ 维满秩的向量空间数量即可。

这是一个经典问题，考虑每个向量空间一定可以进行 $n$ 次以下步骤之一来唯一得到：

• 添加一个与已有向量线性有关的向量。假设当前秩为 $t$，则方案数为 $2^t$。

• 添加一个与已有向量线性无关的向量，使秩增加 $1$（需要恰好被进行 $k$ 次）。假设当前秩为 $t$，则方案数为 $2^k-2^t$。

写成生成函数即：

$$p_k=\prod\limits_{i=0}^{k-1} (2^m-2^i) [x^{n-k}] \prod\limits_{i=0}^k \dfrac{1}{1-2^ix}$$

前面数量容易计算，后面即 q-binomial 的形式，为 $\dbinom{n}{k}_2$，可以递推算出。该部分时间复杂度 $O(m)$。

第二个问题，最大子集异或和就是所有基底的异或和。那么分每一位考虑，比 $x_k$ 高的位全都为 $0$，主元位必定为 $1$，非主元位有一半的概率为 $1$，故期望为：

$$\dfrac{2^{k+1}-1+\sum\limits_{i=1}^k 2^{x_i}}{2}$$

第三个问题，从低位到高位逐个确定每个基底。那么对于第 $i$ 个基底，后面的 $x_i$ 个位置有 $i-1$ 个是主元位必须为 $0$，其它都可以任意选。故方案数为：

$$\prod\limits_{i=1}^k 2^{x_i-(i-1)}$$

---

全部组合起来，答案为：

$$\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} p_k \dfrac{2^{k+1}-1+\sum\limits_{i=1}^k 2^{x_i}}{2} \prod\limits_{i=1}^k 2^{x_i-(i-1)}=\sum\limits_{k=1}^m p_k2^{-k(k-1)/2-1} \sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} (2^{k+1}-1+\sum\limits_{i=1}^k 2^{x_i}) \prod\limits_{i=1}^k 2^x_i$$

那么只需要对每个 $k$ 计算：

$$f_k=\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} \prod\limits_{i=1}^k 2^{x_i}$$

$$g_k=\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} (\sum\limits_{i=1}^k 2^{x_i}) \prod\limits_{i=1}^k 2^{x_i}$$

$$h_k=\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} x_k \prod\limits_{i=1}^k 2^{x_i}$$

先考虑 $g_k$，巧妙变形：

$$\begin{aligned} g_k&=\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} (\sum\limits_{i=1}^k 2^{x_i}) \prod\limits_{i=1}^k 2^{x_i}\\ &=\sum\limits_{0 \leq x_1 \leq \cdots \leq x_k \leq m-1} (2^m-1-\sum\limits_{i \notin X} 2^{x_i}) \prod\limits_{i=1}^k 2^{x_i}\\ &=(2^m-1)f_k-(k+1) \sum\limits_{0 \leq x_1 \leq \cdots \leq x_{k+1} \leq m-1} \prod\limits_{i=1}^{k+1} 2^{x_i}\\ &=(2^m-1)f_k-g_{k+1}\\ \end{aligned}$$

于是只需快速计算 $f_k$ 及 $h_k$ 即可。

对 $f_k$ 写出生成函数即：

$$F(x)=\prod\limits_{i=0}^{m-1} (1+2^ix)$$

还是 q-analog 那一套，代入 $2x$：

$$(1+2^{m}x) F(2x)=(1+x) F(x)$$

$$f_i(2^i-1)=f_{i-1}(2^m-2^{i-1})$$

线性递推即可。

对 $h_k$ 写出生成函数即：

$$H(x)=\sum\limits_{k=0}^{m-1} 4^kx \prod\limits_{i=0}^{k-1} (1+2^ix)$$

$$\begin{aligned} H(2x)&=\sum\limits_{k=0}^{m-1} 4^k \cdot 2x \prod\limits_{i=0}^{k-1} (1+2^{i+1} x)\\ &=\dfrac{2}{4(1+x)} \sum\limits_{k=0}^{m-1} 4^{k+1} x \prod\limits_{i=0}^{k} (1+2^i x)\\ &=\dfrac{1}{2(1+x)} \sum\limits_{k=1}^{m} 4^{k} x \prod\limits_{i=0}^{k-1} (1+2^i x)\\ &=\dfrac{1}{2(1+x)} \Big[ \sum\limits_{k=0}^{m-1} 4^{k} x \prod\limits_{i=0}^{k-1} (1+2^i x) -1+4^mx \prod\limits_{i=0}^{m-1} (1+2^ix) \Big]\\ &=\dfrac{1}{2(1+x)} \Big[ \sum\limits_{k=0}^{m-1} 4^{k} x H(x)-1+4^mx F(x) \Big]\\ \end{aligned}$$

$$2(1+x)H(2x)=\sum\limits_{k=0}^{m-1} 4^{k} x H(x)-1+4^mx F(x)$$

$$(2^{i+1}-1) h_i=4^m f_{i-1}-2^i h_{i-1}-[i=1],i \geq 1$$

同样可以线性递推。

总时间复杂度 $O(m)$。

官方题解到处都是 NTT，错过了普及 q-analog 的大好机会

AGC041D Problem Scores (3100)

显然对于某个 $k$，只需要考虑前缀 $k+1$ 个数 $pre_{k+1}$ 之和大于后缀 $k$ 个数 $suf_{n-k+1}$ 之和的限制。

设 $s_k=pre_{k+1}-suf_{n-k+1}$，差分有 $s_k-s_{k-1}=a_k-a_{n-k+1}$。而 $\{a_i\}$ 单调不降，故 $k=\lfloor \dfrac{n-1}{2} \rfloor$ 时 $s_k$ 是最小的，只需考虑此限制即可。

由于要求 $\{a_i\}$ 单调不降，设 $\{a_i\}$ 的差分数组为 $\{b_i\}$，考虑 $b_i$ 对 $s_k$ 的贡献：

• $n$ 为奇数：$\{1,0,-1,-2,\cdots,-k+1 \ , \ -k,-k+1,\cdots,-1\}$。

• $n$ 为偶数：$\{1,0,-1,-2,\cdots,-k+1 \ ,-k, \ -k,-k+1,\cdots,-1\}$。

记此贡献系数为 $c_i$。可以看到 $b_1$ 比较特殊，考虑枚举 $b_2,\cdots,b_n$ 再算 $b_1$ 的取值方案数。限制即：

$$b_1 \leq n-\sum\limits_{i=2}^n b_i$$

$$b_1 > \sum\limits_{i=2}^n c_ib_i$$

故 $b_1$ 共 $\max(0,n-\sum\limits_{i=2}^n (c_i+1) b_i)$ 种取值方案。

对所有 $(c_i+1)$ 做完全背包即可，时间复杂度 $O(n^2)$。可以同 P4389 付公主的背包 用分治乘优化到 $O(n \log^2 n)$。

ARC111F Do you like query problems? (3100)

可以对每个位置分别考虑，可以线性得到贡献为关于 $x=i(n+1-i)$ 的 $q$ 次多项式，但无法避免插值（不过足以通过）。

更聪明的做法，首先对值域将期望拆成概率。枚举 $w \in [0,m)$，将所有 $\geq w$ 的数视为 $1$，其它数视为 $0$，计算答案后全部求和即可得到原问题答案。

将修改和询问分别考虑。考虑计算 $t$ 次操作后第 $i$ 个数为 $1$ 的概率 $f_{w,t,i}$。注意到只有两种修改会影响 $a_i$ 的取值，称作关键操作：

• 第一类操作，$i \in [l,r],v<w$。

• 第二类操作，$i \in [l,r],v \geq w$。

于是 $a_i$ 由最后一次关键操作决定。而一次操作为关键操作的概率为：

$$p_i=\dfrac{i(n-i+1)}{n(n+1)/2} \cdot \dfrac{2m}{2m+1} \cdot \dfrac{1}{2}(\dfrac{w}{m}+\dfrac{m-w}{m})=\dfrac{i(n-i+1)}{n(n+1)/2} \cdot \dfrac{m}{2m+1}$$

若前 $t$ 次操作中没有关键操作，则 $a_i$ 为 $0$。否则有 $\dfrac{m-w}{m}$ 的概率 $a_i$ 为 $1$。故

$$f_{w,t,i}=\dfrac{m-w}{m}[1-(1-p_i)^t]$$

先在这里对 $w$ 求和，有：

$$g_{t,i}=\sum\limits_{w=0}^{m-1} f_{w,t,i}=\dfrac{m-1}{2}[1-(1-p_i)^t]$$

考虑上一次操作为第三种操作（即询问）的概率，答案即为：

$$\begin{aligned} Ans&=\sum\limits_{t=0}^{q-1} \sum\limits_{i=1}^n \dfrac{i(n-i+1)}{n(n+1)/2} \dfrac{1}{2m+1} \cdot \dfrac{m-1}{2}[1-(1-p_i)^t]\\ &=\sum\limits_{i=1}^n \dfrac{i(n-i+1)}{n(n+1)} \dfrac{m-1}{2m+1} \sum\limits_{t=0}^{q-1} [1-(1-p_i)^t]\\ &=\sum\limits_{i=1}^n \dfrac{i(n-i+1)}{n(n+1)} \dfrac{m-1}{2m+1} (q-\dfrac{1-(1-p_i)^q}{p_i})\\ \end{aligned}$$

预处理即可做到 $O(n \log q)$。

AGC003F Fraction of Fractal (3300)

设迭代了 $k$ 次的图形为 $G_k$（初始图形为 $G_1$）。

考虑 $G_2$，显然应当关注上下/左右边界能否相接。

• 若上下及左右边界均相接，则答案为 $1$。

• 若上下及左右边界均不相接，则每个小块都是一个联通块。设图 $G_1$ 中共 $s$ 个黑格，则答案为 $s^{k-1}$。

否则考虑左右相接而上下不相接的情况。设 $G_1$ 左右边界上有 $p$ 个格子相接，那么 $G_k$ 的左右边界上有 $p^k$ 个格子相接。

考虑迭代 $k$ 次，相当于将 $G_1$ 的每个黑格替换为 $G_{k-1}$。由于上下不相接，所以每一行是独立的。

那么一行中连续的 $t$ 个黑格全部替换为 $G_{k-1}$ 后，得到的联通块数量即为 $tf_{k-1}-p^{k-1}$。

设所有行的连续段长度之和为 $A$，数量为 $B$，则有递推式：

$$f_0=1,f_k=Af_{k-1}-B p^{k-1}$$

当然可以直接写矩阵快速幂求出。

懒得写怎么办呢？ Bonus：$k \leq 10^{10^5}$。

写成生成函数就是 $F(x)=AxF(x)-\dfrac{Bx}{1-x}+1$，即 $F(x)=\dfrac{1-(p+B)x}{(1-px)(1-Ax)}$。

部分分式化后解得：

$$f_k= \begin{cases} \dfrac{Bp^k+(A-p-B)A^k}{A-p},A \neq p\\ (k+1)A^k-k(A+B)A^{k-1},A=p \end{cases}$$

时间复杂度 $O(\log k)$。

ARC142D Deterministic Placing (2900)

场上被 C 卡死了，这题要是时间充裕就搞出来了

首先注意到操作可逆，也即若在情况间连转移边，所有合法的情况一定形如若干二元环。

考虑合法情况 $A$，将每个棋子向移动到的点连边，显然会连出若干条链。这些链必须覆盖所有点，否则空点的邻居就可以改为移向空点，不合法。

注意到 $A$ 的所有链尾都没有棋子，而其转移到的状态 $B$ 的所有链头都没有棋子。而若某条链的链头 $u$ 与另一条链的非链头 $v$ 相邻，$v$ 就可以在 $A,B$ 状态之一中移向 $u$，不合法。

容易发现在这两个限制下一定是合法的。

于是一个情况合法的充要条件为：

• 所有的链恰好覆盖了树上的所有点。

• 每条链的链头的邻居都为某条链的链头，每条链的链尾的邻居都为某条链的链尾。

那么设计一个树形依赖背包 DP 即可。设 $f_{u,0/1/2}$ 分别表示 $u$ 号点不是端点，当前连接了下面连上来的 $0/1/2$ 条链的方案数。$g_{u,0/1}$ 分别表示 $u$ 号点是端点，当前连接了下面连上来的 $0/1$ 条链的方案数（$g_{u,1}$ 是实际方案数除二，这是为了在给 $f$ 转移只有一种选择）。那么有转移：

$$g_{u,1} \leftarrow g_{u,0}f_{v,1}+g_{u,1}f_{v,1}$$

$$g_{u,0} \leftarrow g_{u,0}g_{v,1}$$

$$f_{u,2} \leftarrow f_{u,2}f_{v,2}+2f_{u,1}f_{v,1}$$

$$f_{u,1} \leftarrow f_{u,0}f_{v,1}+f_{u,1}f_{v,2}$$

$$f_{u,0} \leftarrow f_{u,0}f_{v,2}$$

在 u 的转移结束后，还要转移 $f_{u,1} \leftarrow f_{u,1}+g_{u,0}$。

时间复杂度 $O(n)$。

AGC040D Balance Beam (3500)

容易发现若 Ringo 的起始点为 $x$ 时 Snuke 能够追上 Ringo，则起始点为 $y(y<x)$ 时也能。故使 Snuke 获胜的起始点一定是一段前缀。

下面设 $a_t,b_t$ 分别表示点 $t$ 所在的整段的 $A$ 值与 $B$ 值。

考虑起始点为 $x$，Snuke 在 $y$ 处追上 Ringo。则需要满足：

$$-\int_0^x a_t dt+\int_x^y(b_t-a_t) dt \geq 0$$

显然 $y$ 所在的整段 $k$ 一定满足 $A_k<B_k$，故 $\lceil y \rceil$ 也一定满足条件，故不妨设 $y$ 为整点。

假设 $x$ 只能为整点（即求答案向下取整的值），那么问题相当于在所有整段中选出两个不交的集合 $S_1,S_2$ 满足 $s=-\sum_{i \in S_1} A_i+\sum_{i \in S_2} (B_i-A_i) \geq 0$，最大化 $|S_1|$。可以设计这样一个算法：

• 对于每个整段 $k$，先将其放入 $S_2$ 或者丢掉，再赋权值 $c_k$ 表示将其改为放入 $S_1$ 新增的代价（即让 $s$ 减少多少）。

  • 若 $A_k \leq B_k$，则先将 $k$ 选入 $S_2$ 中使 $s$ 获得 $B_k-A_k$ 的值，$c_k=B_k$。
  • 若 $A_k > B_k$，则先将其丢掉，$c_k=A_k$。

• 将所有 $c_k$ 从小到大排序，若当前 $s \geq c_k$ 则选入并令 $s \leftarrow s-c_k$，否则报告答案退出。

对于原问题，枚举选择一个整段 $k$ 作为 $x$ 所在的整段。设 $p=x-\lfloor x \rfloor=\{x\}$，那么其对 $s$ 的贡献为 $-pA_k+(1-p)(B_k-A_k)$。

令初始 $s=B_k-A_k$，对剩下的 $n-1$ 个整段进行上述算法，即可计算通过得到 $p$ 以及答案。对所有 $k$ 的答案取 $\max$ 即可。

预处理前缀和后可以二分优化算法的第二步，时间复杂度 $O(n \log n)$。

注意分数比较时可能会爆 $\text{long long}$。

ABC257Ex Dice Sum 2 (3500)

显然答案只与每个骰子六个面的和 $S_i$ 及平方和 $Q_i$ 有关（考虑指数型生成函数）。

考虑计算买了某 $k$ 个骰子的期望收益，拆括号算（也可以用概率型生成函数）。下面的变量 $i,j$ 都是在这 $k$ 个骰子中枚举：

$$\begin{aligned} S&=\dfrac{1}{6^k} \Big( \sum\limits_{i,p} 6^{k-1} A_{i,p}^2 +2 \sum\limits_{i \neq j,p,q} 6^{k-2}A_{i,p}A_{j,q}\ \Big)-\sum\limits_i C_i\\ &=\dfrac{1}{6} \sum\limits_{i,p} 6^{k-1} A_{i,p}^2+\dfrac{1}{18} \cdot \dfrac{1}{2} \big[ (\sum\limits_{i,p} A_{i,p})^2-\sum\limits_{i}(\sum\limits_{p} A_{i,p})^2 \big]\\ &=\dfrac{1}{36} (\sum\limits_{i} S_i)^2+\dfrac{1}{6} \sum\limits_{i} Q_i-\dfrac{1}{36} \sum\limits_{i} S_i^2-\sum\limits_i C_i\\ \end{aligned}$$

记 $B_i=6 \sum\limits_{i} Q_i-\sum\limits_{i} S_i^2-36 \sum\limits_i C_i$，则 $S=\dfrac{1}{36} \Big[ (\sum\limits_{i} S_i)^2+\sum\limits_{i} B_i \Big]$。

显然最难处理的就是这个平方项。考虑一个神奇的想法：将两个 $(\sum\limits_{i} S_i)$ 中的一个换成变量 $x$，这样枚举 $x$ 就只需要处理关于 $x$ 的一次函数即可。（正确性见下方证明）

于是 $36S=\sum\limits_{i} (S_ix+B_i)$。对于一个固定的 $x$，将 $n$ 个骰子按这个值排序后取最大的 $k$ 个统计答案即可（注意是按 $36S=(\sum\limits_{i} S_i)^2+\sum\limits_{i} B_i$ 统计，因为 $x$ 不一定是 $\sum S_i$）。

那么只需要维护函数值间的大小关系即可。考虑令 $x$ 从小到大扫描，任意两根直线间至多只有一个交点，这两个函数值的大小关系也只会变化一次。求出所有交点后维护所有函数值的大小关系，统计答案即可。

具体实现，可以维护一个有向完全图表示大小关系（$u$ 连向 $v$ 表示 $u$ 大于 $v$），那么只需要统计入度 $<k$ 的直线的函数值之和即可。注意交点的 $x$ 坐标可能重复，意味着函数值可能相等。我们不在这种情况下统计答案（会算重），于是再对入度开一个桶判重即可。

时间复杂度 $O(n^2+\text{sort}(n^2))$。

---

正确性证明（不保证正确）：设最优解的 $S,B$ 之和分别为 $S_1,B_1$。令 $x=2S_1$，假设存在另一组解 $S_2,B_2$ 满足：

$$S_2x+B_2>S_1x+B_1,S_2^2+B_2<S_1^2+B_1$$

$$2S_1^2-2S_1S_2<B_2-B_1<S_1^2-S_2^2$$

$$(S_1-S_2)^2<0$$

显然矛盾。故一定会被枚举到最优解之一。

AGC031D A Sequence of Permutations (3100)

设 $f(p,q)=r$，则 $r_{p_i}=q_i$，$r_{i}=q_{p^{-1}_i}$，即 $r=q \circ p^{-1}$。

写出前几项看看（下面省略复合符号）：

$$a_1=p\\ a_2=q\\ a_3=q p^{-1}\\ a_4=q \underline{p^{-1}} q^{-1}\\ a_5=q p^{-1} \underline{q^{-1}} p q^{-1}\\ a_6=q p^{-1} \underline{q^{-1} p} p q^{-1}\\ a_7=q p^{-1} q^{-1} p \underline{p} p^{-1} q p q^{-1}\\ a_8=q p^{-1} q^{-1} p \underline{q} p^{-1} q p q^{-1}\\ a_9=q p^{-1} q^{-1} p \underline{q p^{-1}} p^{-1} q p q^{-1}\\ \cdots$$

规律十分显然。设 $V=q p^{-1} q^{-1} p$，下面归纳证明：

• 当 $i \in [1,4]$，$a_{6k+i}=V^t a_i V^{-t},a_{6k+i+1}=V^t a_{i+1} V^{-t} \Rightarrow a_{6k+i+2}=V^t a_{i+1} V^{-t} V^t a_i^{-1} V^{-t}=V^t a_{i+2} V^{-t}$。

• $a_{6k+5}=V^t a_5 V^{-t},a_{6k+6}=V^t a_6 V^{-t} \Rightarrow a_{6k+7}=V^t a_7 V^{-t}=V^{t+1} p V^{-t-1}$。

• $a_{6k+6}=V^t a_6 V^{-t},a_{6k+7}=V^t a_7 V^{-t} \Rightarrow a_{6k+8}=V^t a_8 V^{-t}=V^{t+1} q V^{-t-1}$。

于是只需要计算复合及 $k$ 次复合即可。不需要快速幂，将置换拆成若干个循环，可以快速算出每个循环的答案。

时间复杂度 $O(n)$。

所以为什么所有题解写的都是快速幂，也没多麻烦吧

ARC144D AND OR Equation (2500)

按每一位分别考虑。注意到对于第 $t$ 位不为的二进制数 $S$，$f(S)+f(2^t)=f(S+2^t)+f(0)$，即 $f(S+2^t)-f(S)=f(2^t)-f(0)$。

记 $w_t=f(2^t)-f(0)$，可推知 $f(S)=\sum\limits_{i \in S} w_i$，同时容易验证该函数是合法的。

那么接下来只需要数 $\{f(0),w_0,\cdots,w_{n-1}\}$ 即可，需要满足 $f(0) \in [0,k],f(0)+\sum\limits_{i=0}^{n-1} |w_i| \leq k$。

写成生成函数即：

$$\begin{aligned} Ans &= \sum\limits_{i=0}^k [x^i]\dfrac{1}{1-x} (1+2x+2x^2+\cdots)^n\\ &=[x^k] \dfrac{1}{(1-x)^2} (\dfrac{2}{1-x}-1)^n\\ &=\sum\limits_{i=0}^n 2^i(-1)^{n-i} \dbinom{k+i+1}{k} \\ \end{aligned}$$

时间复杂度 $O(n)$。

ABC260Ex Colorfulness (3300)

看错题想了一晚上

$k$ 次方之和看起来很不可做而且一看就是二合一，假装没有。下面对每个 $k$ 计算 $C(P)=k$ 的排列个数 $s_k$。

设第 $i$ 种颜色有 $m_i$ 个球。

枚举颜色的所有排列，相当于让同种颜色的球不区分了。故对于一种颜色排列，其对应的原排列都有 $\prod\limits_{i} m_i!$ 种。

那么只需要对每个 $k$ 数恰有 $k$ 个连续段的颜色排列数量即可。

这是个经典问题，设 $g_k$ 表示钦定有 $k$ 个相邻位置颜色相同，通过二项式反演即可得到答案。

对每种颜色 $i$，钦定有 $c_i$ 个相邻颜色相同。那么总方案数是：

$$\dbinom{n-\sum\limits_{c_i}}{m_1-c_1,\cdots,m_n-c_n} \prod\limits_{i=1}^{n} \dbinom{m_i-1}{c_i}$$

分治 NTT 卷一卷即可得到。该部分时间复杂度 $O(n \log^2 n)$。

那对于二合一的后半部分，已经板到不能再板了，写成生成函数的形式，再交换和号，算一算分式求和即可做到 $O(n \log^2 n+m \log m)$。

总时间复杂度 $O(n \log^2 n+m \log m)$。

AGC024F Sequence Growing Hard (3000)

为了避免边界问题，在每个序列的末尾补一个 $0$。

考虑怎样的插入是合法的。设插入的数为 $x$，其后面的数为 $y$，则：

• 若 $x<y$，则一定不合法。

• 若 $x>y$，则一定合法。

• 若 $x=y$，设 $y$ 后第一个不与 $y$ 相同的数为 $k$。若 $y<k$ 则不合法，否则合法。

注意到第 $3$ 种情况其实与在 $k$ 前插入 $x$ 是等价的，其恰能转化为第一或第二种情况之一。故只考虑前两种情况即可不重不漏。

那么现在问题变为每次在某个数 $y$ 前插入 $x(x>y)$。于是若由 $y$ 向 $x$ 连边（数间连边，非值间连边），那么最后会形成一棵大小为 $n+1$ 的有根树。它满足：

• 根的权值为 $0$，树的每个非根节点的权值大于其父亲权值。

• 每个非叶节点的儿子有序。

那么只需要对树计数即可。设 $f_{i,j}$ 表示树根的值为 $i$，共有 $j$ 个点的方案数；$g_{i,j}$ 表示 $f_{i,j}$ 关于 $i$ 的后缀和。转移时用 $f_{i,t}$ 和 $g_{i+1,j-t}$ 拼在一起即可。

注意一棵树不一定只对应一个合法序列，实际上数的是其特殊拓扑序的数量，拓扑序要满足：

• 每个点的拓扑序比其所有儿子拓扑序小。

• 每个点靠右儿子的拓扑序比靠左儿子的拓扑序小。

计数时可以看做从右到左枚举每个儿子 $v$，先把 $v$ 的子树中除了 $v$ 的加入并与先前的可重排，再加入 $v$。于是实际转移式是：

$$f_{i,j} \leftarrow [j=1]+\sum\limits_{t=1}^{j-1} \dbinom{j-2}{t-1} f_{i,t} g_{i-1,j-t}$$

时间复杂度 $O(kn^2)$。

令 $h_{i,j}=f_{i,j+1}$，则：

$$h_{i,j} \leftarrow [j=0]+\sum\limits_{t=0}^{j-1} \dbinom{j-1}{t} h_{i,t} g_{i-1,j-t}$$

那么可以用分治 NTT 做到 $O(kn \log^2 n)$。

（不保证正确）写出来大概是一个类似 $H'=HP+1$ 的东西，也许可以解微分方程做到 $O(kn \log n)$？

AGC004E Salvage Robots (3200)

这么多机器人一起动很麻烦，看作是出口带着墙壁一起动，墙壁撞到机器人就清除掉了。

考虑出口已经走过的地方。如果走过一步后走过的区域的横纵坐标最小最大值没有变，那么不会有机器人挂掉。

所以整个过程相当于维护一个矩形，每次向上下左右某个方向拓展一条边，并将这条边上还活着的机器人救下。

那么直接二维区间 DP 维护这个过程即可。时间复杂度 $O(n^2 m^2)$。

ABC258Ex Odd Steps (2800) | AGC013E Placing Squares (3500)

2017 *3500=2022 *2800

写一个不需要任何组合意义的暴力代数做法。

ABC258Ex Odd Steps

考虑只有 $S$ 的限制的方案数。写成生成函数即：

$$\begin{aligned} F(x)&=\dfrac{1}{1-\dfrac{x}{1-x^2}}\\ &=\dfrac{1-x^2}{1-x^2-x}\\ &=1+\dfrac{x}{1-x-x^2}\\ \end{aligned}$$

熟悉斐波那契数的同学都知道，这就是斐波那契数的生成函数。

熟悉斐波那契数的同学都知道，斐波那契数的通项公式是：

$$fib_n=\dfrac{1}{\sqrt 5}[(\dfrac{1+\sqrt 5}{2})^n-(\dfrac{1-\sqrt 5}{2})^n]=\dfrac{1}{\sqrt 5}(A^n-B^n)$$

对于限制，容斥钦定一个点集 $S$ 必须经过。考虑设 $f_i$ 表示考虑前 $i$ 个点，钦定经过第 $i$ 个点的方案数，有：

$$f_i=-\sum\limits_{j=0}^{i-1} fib_{a_i-a_j} f_j=\dfrac{1}{\sqrt 5} (A^{a_i} \sum\limits_{j=0}^{i-1} A^{-a_j} f_j-B^{a_i} \sum\limits_{j=0}^{i-1} B^{-a_j} f_j)$$

前缀和优化即可。时间复杂度 $O(n \log S)$。

不过 $5$ 在模 $998244353$ 下没有二次剩余，还需要拓域。

---

AGC013E Placing Squares

还是先考虑没有限制的情况。

先写出 $F(x)=\sum_{i=0} i^2 x^i$ 的封闭形式。由 $k^2=2\dbinom{k+2}{2}-3\dbinom{k+1}{1}+\dbinom{k}{0}$，可以得到：

$$F(x)=\dfrac{2}{(1-x)^3}-\dfrac{3}{(1-x)^2}+\dfrac{1}{1-x}$$

于是答案的生成函数为：

$$G(x)=\dfrac{1}{1-F(x)}=\dfrac{(1-x)^3}{-x^3+2x^2-4x+1}$$

化为线性递推形式即：

$$g_0=0,g_1=1,g_2=5,g_k=4g_{k-1}-2g_{k-2}+g_{k-3}$$

记矩阵 $M$ 的第三行第一列值为 $v(M)$。

故可以写成矩阵快速幂形式 $g_k=v(A^kP)$。同样的：

$$f_i=v\big( -\sum\limits_{j=0}^{i-1} f_j A^{x_i-x_j} P \big)=v\big( A^{x_i} (\sum\limits_{j=0}^{i-1} f_j A^{-x_j}) P \big)$$

$A$ 是有逆矩阵的，前缀和优化即可。时间复杂度 $O(m \log n)$。

ARC120F/F2 Wine Thief (3100/???)

Easy Version

Sol1（官方题解）：

这个是怎么想到的

显然求出每个酒瓶被选中的次数 $ans_i$ 即可。

记序列上的总方案数为 $p_{n,k}=\dbinom{n-k+1}{k}$，环上总方案数为 $q_{n,k}=p_{n-1,k}+p_{n-3,k-1}$（枚举第一个酒瓶是否选）。

注意到如果问题在环上，那么每个位置的方案数都是相等的。棘手的地方在于所有酒瓶排成一个序列而不是环。

考虑先计算环的方案数，再将不满足环但满足序列的方案补上。可以设计这样一个算法：

• 初始令 $l=1,r=n$。记 $len=r-l+1$。
• 将 $ans_l,ans_{l+1},\cdots,ans_r$ 都加上 $\dfrac{len}{n} q_{len,k}$。（环的方案数）
• 将 $ans_l,ans_r$ 加上 $f_{len-4,k-2}$。（同时选了 $l,r$，对 $ans_l,ans_r$ 的贡献）
• 令 $l \leftarrow l+2,r \leftarrow r-2,k \leftarrow k-2$，重复进行。（同时选了 $l,r$，对 $ans_{l+2},\cdots,ans_{r-2}$ 的贡献）

维护差分数组即可，时间复杂度 $O(n)$。

注意当 $l=r,k=1$ 时 $q_{1,1}=0$，但应该计入方案中，需要特判。

Sol2：

这才是正确的做法

这里先假设 $d$ 不一定等于 $2$。记序列上的总方案数为 $p_{n,k}=\dbinom{n-(d-1)(k-1)}{k}$

考虑 DP。设 $f_{n,k,i}$ 表示在 $n$ 个酒瓶中选 $k$ 个，第 $i$ 个被选中的次数。

第 $i$ 个被选中，要求 $i-d \sim i-1$ 及 $i+1 \sim i+d$ 均不能被选。但直接将两边删去会造成额外的限制。

考虑只删去 $i \sim i+d$，再要求 $i-d \sim i-1$ 不能选，这样限制是正确的。又由于 $i-d \sim i-1$ 中至多只能选一个，可以得到：

$$f_{n,k,i}=p_{n-d,k-1}-\sum\limits_{j=\max(1,i-d)}^{i-1} f_{n-d,k-1,j}$$

那么当 $d=2$ 时，就是：

$$f_{n,k,i}=p_{n-2,k-1}-f_{n-2,k-1,i-1}=p_{n-2,k-1}-p_{n-3,k-2}+f_{n-3,k-2,i-2}=\cdots$$

对于每个 $i$，前面的部分都是一样的，而最后的 $f_{n',k',1}=p_{n'-2,k'-1}$ 容易计算。

时间复杂度 $O(n)$。

Hard Version

书接上文，有：

$$f_{n,k,i}=p_{n-d,k-1}-\sum\limits_{j=\max(1,i-d)}^{i-1} f_{n-d,k-1,j}$$

我们只关心 $f_{n-dt,k-t}$ 处的值。写出生成函数，记 $F_t(x)=\sum\limits_{i=1}^{n-dt} f_{n-dt,k-t,i} x^i$。那么转移即：

$$F_t(x)=-F_{t+1}(x) \sum\limits_{i=1}^{d-1} x^i + p_{n-d(t+1),k-(t+1)} \sum\limits_{i=1}^{n-dt} x^i$$

记 $m=\min(\lfloor \dfrac{n}{d} \rfloor,k-1)$，边界条件即 $F_m(x)=\sum\limits_{i=1}^{n-dm} x^i$。

记 $V(x)=-\sum\limits_{i=1}^{d-1} x^i$，$w_t=p_{n-d(t+1),k-(t+1)}$，$P_t(x)=w_t \sum\limits_{i=1}^{n-dt} x^i$。于是：

$$\begin{aligned} F_t(x)&=F_{t+1}(x)V(x)+P_t(x)\\ &=F_{t+2}(x)V^2(x)+P_{t+1}(x)V(x)+P_t(x)\\ &=\cdots\\ &=\sum\limits_{i=t}^m P_i(x) V(x)^{i-t} \end{aligned}$$

只需要计算：

$$F_0(x)=\sum\limits_{i=0}^m P_i(x) V(x)^{i}$$

这可以分治 NTT 解决。

当然这和普通的分治 NTT 不太一样：

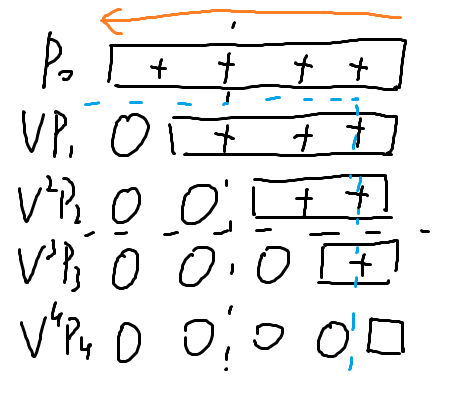
如图。圆圈表示 $V$，方框表示 $P$（内部是加号），右边为低位。注意一行中每一块是 $d$ 次多项式。

先抛掉蓝色范围外的部分（最后加上即可）。记 $P_{l,r}(x)$ 表示圆圈（不带 $w$）的乘积（即 $V^{r-l+1}$），$Q_{l,r}(x)$ 表示 $l \sim r$ 行每行圆圈乘积（带 $w$）之和，$R_{l,r}(x)$ 表示范围内的答案（钦定方框的最低位为 $x^0$）。

$$P_{l,r}(x)=P_{l,mid}(x) P_{mid+1,r}(x)$$

$$Q_{l,r}(x)=P_{l,mid}(x) Q_{mid+1,r}(x)+Q_{l,mid}(x)$$

$$R_{l,r}(x)=P_{l,mid}(x) R_{mid+1,r}(x)+Q_{l,mid}(x) \sum\limits_{i=1}^{d(r-mid)} x^i+x^{r-mid} (R_{l,mid}(x)-w_{mid} P_{l,mid}(x))$$

总时间复杂度 $O(n \log n \log \dfrac{n}{d})$。

注意 $k=1$ 时会导致 $m=0$，特判即可。

这 n 是怎么敢出到 1e6 的，如果被卡常了可以考虑特判掉 $d=2$。

AGC015E Mr.Aoki Incubator (3600)

又看错题了，以为速度可以为负，又想了一晚上

下面称变成 Aoki 的 Takahashi 为被标记的。

结论：设若初始标记集合 $S$，最终被标记的人集合为 $f(S)$，那么 $f(S \bigcup T)=f(S) \bigcup f(T)$。

证明：假设最终有一个人 $x \notin f(S) \bigcup f(T)$，那么他不可能初始被标记，且标记他的人 $x'$ 同样满足 $x' \notin f(S) \bigcup f(T)$……无限递归下去，而这个过程是有限的，故假设矛盾。

那么考虑只标记一个人 $x$，最终被标记的是哪些。

首先在 $x$ 右边且比 $x$ 慢的会被标记，在 $x$ 左边且比 $x$ 快的会被标记。

但不仅如此。在 $x$ 左边且比 $x$ 快的超过 $x$ 后会将右边比它们慢的标记，同样在 $x$ 右边且比 $x$ 慢的会将左边比它们快的标记。容易发现新增的这些不会标记更多的人。

将所有人按坐标排序，记速度的前缀最大值为 $pmx_x$，后缀最小值为 $smn_x$，那么被标记的人是：

• $x$ 本身。
• 在 $x$ 左边，且比 $smn_x$ 严格快的人。
• 在 $x$ 右边，且比 $pmx_x$ 严格慢的人。

设 $dp_i$ 表示考虑前 $i$ 个人，初始标记了第 $i$ 个人的方案数。

假设由 $j$ 转移而来（上一个初始标记的是 $j$），那么覆盖不到的区域是位置在 $(j,i)$ 的人且速度在 $[pmx_j,smn_i]$ 中的人。

由于 $pmn,pmx$ 都是单调不降的，故对于一个 $i$ 而言 $j$ 具有可二分性。那么维护能转移的最小的 $j$，其具有单调性。

用 Two-pointer 维护即可，同时类似莫队维护检查的矩形。时间复杂度 $O(\text{sort}(n))$。

AGC002F Leftmost Ball (3400)

考虑先枚举 $0$ 色点的位置。那么计算方案时从右往左，每遇到一个 $0$ 色点就在前面的数中抽 $k-1$ 个出来。

直接 DP 只能做到 $O(n^2k)$，没有前途。

换一个思路，不定顺序，而是全局一种一种颜色地加。为了避免算重，还要定一个加入颜色的顺序。

不妨将每种非 $0$ 颜色的第一个位置拿出来并按位置排序，按照这个顺序加入。这样相当于每次加入新颜色都要求新加入的第一个位置前面都填 $0$。

这样貌似已经可以做了，不过一个更巧妙的处理是将 $0$ 色点与其它颜色分开处理。即每次加入是以下两种之一：

• 将第一个未染色的位置变成 $0$。
• 将包含第一个位置的某 $k-1$ 个位置染成一种新颜色（要求染完后非 $0$ 颜色数不能超过 $0$ 个数）。

那么设 $f_{i,j}(i \geq j)$ 表示已加入 $i$ 个 $0$，$j$ 种非 $0$ 颜色。转移为：

$$f_{i,j} \leftarrow f_{i-1,j}+(n-j+1) \dbinom{nk-i-(j-1)(k-1)}{k-2} f_{i,j-1}$$

时间复杂度 $O(n(n+k))$。

注意 $k=1$ 时比较特殊，要特判。

ARC145F Modulo Sum of Increasing Sequences (3900)

反演好题，单位根反演在模数较大时还是有用的

称 $p=MOD$。

考虑处理不降的限制，可以计数差分数组。设 $a_{n+1}=m$，差分数组为 $c_1,c_2,\cdots,c_{n+1}$。那么限制即 $c_1+c_2+\cdots+c_{n+1}=m$，而原数和 $s=nc_1+(n-1)c_2+\cdots+c_n$。

写成生成函数即求：

$$[x^m] \prod\limits_{i=0}^n \dfrac{1}{1-y^ix}$$

其中 $y$ 这一维是模 $p$ 的循环卷积。

但这个形式还套个求逆，稍难处理。

可以从另一方面作些转化：令每个 $a_i \leftarrow a_i+i-1$（最后所有都需要减掉 $i(i-1)/2$），则将不降改为单增，相当于在 $0,1,\cdots,n+m-1$ 中选出 $n$ 个数的集合。下面令 $m \leftarrow n+m$，那么即求：

$$[x^n] \prod\limits_{i=0}^{m-1} (1+y^ix)$$

由于 $p$ 很小，我们可以分开整块与零块两部分算。令 $r=m \bmod p$，$m'=m-r$。

枚举零块中选了 $q$ 个数，整块中选了 $n'=n-q$ 个数，那么分别计算：

$$F(y)=[x^{n'}][\prod\limits_{i=0}^{p-1} (1+y^ix)]^{m'/p}$$

$$G(y)=[x^q][\prod\limits_{i=0}^{r-1} (1+y^ix)]$$

---

计算 $F(y)$。循环卷积相当于对每个 $d$ 求 $s_d=\sum_t f_{n',tp+d}$，可以用单位根反演。

记 $\omega$ 为 $p$ 次单位根，先对每个 $d$ 求出 $F(\omega ^d)$。

$d=1$ 时，大家都知道：

$$\prod\limits_{i=0}^{p-1} (1-\omega^ix)=1-x^p$$

这是因为左右都为 $p$ 次多项式且最高项系数相同，且根集均为 $1,\omega,\omega^2,\cdots,\omega^{p-1}$。由因式定理即得左右多项式相同。

当 $d \neq 1$ 时，记 $g=\gcd(d,p)$，那么会有：

$$\prod\limits_{i=0}^{p-1} (1-\omega^{di} x)=[\prod\limits_{i=0}^{p/g-1} (1-\omega^{g i} x)]^g=(1-x^{p/g})^g$$

$$[\prod\limits_{i=0}^{p-1} (1+y^ix)]^{m'/p}=(1-(-x)^{p/g})^{gm'/p}$$

令人惊讶，这是一个整式。二项式展开后 $x^{n'}$ 系数即为 $[(p/g) \mid n'] (-1)^{n'} (-1)^{n'/(p/g)} \dbinom{gm'/p}{n'/(p/g)}$。

$$F(\omega^d)=[(p/g) \mid n'] (-1)^{n'} (-1)^{n'/(p/g)} \dbinom{m'/(p/g)}{n'/(p/g)}$$

然后需要用单位根反演还原系数：

$$s_d=\dfrac{1}{p} \sum\limits_{i=0}^{p-1} \omega^{-id} F(\omega^i)$$

Sol 1（标解）

先别着急拆。注意到 $F(\omega^i)$ 只与 $\gcd(i,p)$ 有关，进行一个莫比乌斯反演：

$$\begin{aligned} s_d &=\dfrac{1}{p} \sum\limits_{g \mid p} F(\omega^g) \sum\limits_{i=0}^{p-1} [\gcd(i,p)=g] \omega^{-id}\\ &=\dfrac{1}{p} \sum\limits_{g \mid p} F(\omega^{g}) \sum\limits_{i=0}^{p/g-1} [\gcd(i,p/g)=1] \omega^{-gid}\\ &=\dfrac{1}{p} \sum\limits_{g \mid p} F(\omega^{g}) \sum\limits_{i=0}^{p/g-1} \omega^{-gid} \sum\limits_{t \mid i, t \mid (p/g)} \mu(t)\\ &=\dfrac{1}{p} \sum\limits_{t \mid p} \mu(t) \sum\limits_{g \mid (p/t)} F(\omega^{g}) \sum\limits_{i=0,t \mid i}^{p/g-1} \omega^{-gid} \\ &=\dfrac{1}{p} \sum\limits_{t \mid p} \mu(t) \sum\limits_{g \mid (p/t)} F(\omega^{g}) \sum\limits_{i=0}^{p/(gt)-1} \omega^{-gtid} \\ &=\dfrac{1}{p} \sum\limits_{t \mid p} \mu(t) \sum\limits_{g \mid (p/t)} F(\omega^{g}) \dfrac{p}{gt} [p \mid gtd]\\ \end{aligned}$$

一共要做 $r$ 次，这里的总复杂度为 $O(p^2d^2(p))$。

Sol 2（暴力）

不推式子，直接计算。当然 $998244353$ 再强大也不可能有 $500$ 次单位根，直接记录下来每个单位根的系数。设 $s_i=\sum\limits_{t=0}^{p-1} c_{i,t} \omega^t$。

但是系数 $s_i$ 一定是整数，但结果可能是若干复数相加的形式。不过，对于某个 $d$，$\sum\limits_{t=1}^{p/d-1} \omega^{td}=-1$，而由 Sol 1 的式子可以知道这些复数一定可以拆成这样的和式相加的形式，接下来需要做的就是化简。

设数组 $e_{i,t}$ 使得 $c_{i,k}=\sum\limits_{t \mid k} e_{i,t}$，则 $s_i=c_{i,0}-\sum\limits_{t=1}^{p-1} e_{i,t}$。

莫比乌斯反演得 $e_{i,k}=\sum\limits_{t \mid k} \mu(k/t) c_{i,t}$，于是：

$$\sum\limits_{k=1}^{p-1} e_{i,k}=\sum\limits_{k=1}^{p-1} \sum\limits_{t \mid k} \mu(k/t) c_{i,t}=\sum\limits_{t=1}^{p-1} c_{i,t} \sum\limits_{t=1}^{\lfloor (p-1)/i \rfloor} \mu(t)$$

可以在 $O(p^2)$ 内完成。

由于需要做 $r$ 次，该部分总时间复杂度 $O(p^3)$。

---

计算 $G(y)$。

直接预处理二元多项式乘积即可，该部分时间复杂度 $O(p^3)$。

---

总时间复杂度 $O(n+m+p^3)$。

AGC020F Arcs on a Circle (???)

为什么没人切啊

经典实数 DP。

不过这道题放的是线段而不是点，线段是跨整数的，故线段间小数部分的限制很复杂，不能直接记录。

可以先 $O(n!)$ 枚举线段间小数部分的大小关系。

考虑断环为链。有一个很聪明的做法：以最长线段的左端点断开。这样不会有线段同时跨过该线段的左右端点，那么两边就独立了。

设 $dp_{i,j,k,S}$ 表示当前考虑到 $[i,i+1)$，能覆盖最远的右端点在 $[j,j+1)$，能覆盖最远的右端点是 $k$，已经放了集合 $S$ 的线段。转移分步枚举添加的线段即可。

总时间复杂度 $O(n!2^n n^2 C^2)$。

AGC021F Trinity (4100)

考虑 DP。从左到右依次加入每一列，设 $f_{i,j}$ 表示考虑前 $i$ 列，共有 $j$ 行已经填了黑格（不考虑空行与其的相对位置）的方案数。

考虑转移，在已经填了黑格的行再填对于 $A$ 而言没有意义。设第 $i$ 列新增了 $k$ 个填了黑格的行，则：

• 若 $k=0$，则只能在之前的 $j$ 行中填数，方案数即 $1+j+j(j-1)/2$。

• 若 $k>0$，分情况讨论：

  • 若最大最小值均在这 $k$ 行之中，那么直接处理前面的 $j$ 行与新增的 $k$ 行的相对顺序即可。即在 $j+k$ 行中选 $k$ 行，那么方案数就是 $\dbinom{j+k}{k}$。

  • 若最大值或最小值在 $k$ 行之中，可以看作在 $j+k$ 行中选 $k+1$ 行，并认为这 $k+1$ 行最上面的一行在前面的 $j$ 行中，下面则是新增的 $k$ 行。那么方案数是 $\dbinom{j+k}{k+1}$。

  • 若最大最小值均不在这 $k$ 行之中，同理方案数 $\dbinom{j+k}{k+2}$。

  • 该部分总转移系数是 $\dbinom{j+k}{k}+2\dbinom{j+k}{k+1}+\dbinom{j+k}{k+2}=\dbinom{j+k+2}{k+2}$。

总转移式是：

$$f_{i,j}=f_{i-1,j}(1+\dbinom{j+1}{2})+\sum\limits_{t=1}^j \dbinom{j+2}{t+2} f_{i-1,j-t}$$

答案为 $\sum\limits_{j=0}^n \dbinom{n}{j} f_{m,j}$。

暴力实现复杂度 $O(nm^2)$，使用 NTT 优化可以做到 $O(nm \log m)$。

事实上还有更好的方法。将转移写成指数型生成函数，可以得到：

$$\dfrac{f_{i,j}}{j!}=\dfrac{f_{i-1,j}}{j!}+\dfrac{f_{i-1,j}}{j!} \cdot \dfrac{j(j+1)}{2}+(j+1)(j+2) \sum\limits_{t=1}^j \dfrac{1}{(t+2)!} \dfrac{f_{i-1,j-t}}{(j-t)!}$$

$$F_i(x)=F_{i-1}(x)+x F'_{i-1}(x)+\dfrac{1}{2} x^2 F''_{i-1}(x)+[(e^x-1-x-\dfrac{x^2}{2})F_{i-1}(x)]''$$

经过一大堆无用的计算得到：

$$F_i(x)=e^x F_{i-1}(x)+(2e^x-x-2)F'_{i-1}(x)+(e^x-1-x)F''_{i-1}(x)$$

那么设 $F_i(x)=\sum\limits_{j=0}^m \sum\limits_{k=0}^m g_{i,j,k} x^j e^{kx}$，可以 $O(m^3)$ 转移。

考虑如何计算答案，考虑 $x^i e^{jx}=\sum\limits_t x^i \dfrac{(jx)^t}{t!}$ 对答案的贡献：

$$\sum\limits_t j^t \dfrac{(i+t)!}{t!} \dbinom{n}{i+t}=\dfrac{n!}{(n-i)!} \sum\limits_t j^t \dbinom{n-i}{t}=(1+j)^{n-1} \dfrac{n!}{(n-i)!}$$

于是总复杂度 $O(n+m^3)$，而且不需要 NTT。

ARC137F Overlaps (3300)

先将所有端点离散化为 $2n$ 个点，只对线段间相对关系计数，最后除掉 $(2n)!/2^n$ 即可。记左右端点分别为左右括号。

设 $f_i$ 表示第 $i$ 个右括号前面的左括号数 $-(i-1)$，有限制 $1 \leq f_i \leq k,f_i \geq f_{i-1}-1,f_n=1$，方案数即 $\prod f_i$。问题变为对所有合法的 $\{f_i\}$ 计算方案数之和。

考虑对第二个条件容斥，即钦定一些 $f_i \leq f_{i-1}-2$，这样的限制形成一些连续段。

设这样的长度为 $i$ 的连续段方案数为 $f_i$，记 $F(x)=\sum\limits_i (-1)^{i-1} f_i x^i$，那么有 $\dfrac{1}{1-S(x)}=F(x)$，$S(x)=1-\dfrac{1}{F(x)}$。可以 $O(n \log n)$ 求出。

$f_i$ 可以用分治乘求出：记 $F_{l,r,id1,id2}$ 表示值域在 $[l,r]$，$l$ 是否选择，$r$ 是否选择的生成函数，直接分治乘即可。时间复杂度 $O(k \log^2 k)$。

注意 $f_n=1$ 的限制导致最后一段需要特殊处理重新求一遍。

总时间复杂度 $O(n \log n+k \log^2 k)$。

ARC118F Growth Rate (3600)

怎么会有人把银牌题出到 NOIP 模拟赛啊

设 $f_{q,i}$ 表示只考虑前 $q$ 个数，$A_q=x$ 的方案数，那么有：

$$F_q(x)=\dfrac{x}{1-x} F_{q-1}(a_qx)$$

而 $F_0(x)=\dfrac{x}{1-x}$，那么求 $\sum\limits_{i=0}^m g_i$，其中：

$$G(x)=x^{\prod_{i=1}^n a_i} \prod\limits_{i=1}^n \dfrac{1}{1-x^{\prod_{j=i}^n a_j}}$$

下面考虑求出 $G(x)/x^{\prod_{i=1}^n a_i}$。

虽然 $G(x)$ 的形式美观，但 $m$ 的值域过大无法直接求解，还是考虑回原来的形式（复合与前缀和）。

考虑倒推，假设现在要求 $S(B,m,k)=\sum\limits_{i=0}^m i^k b_i$。

• 若 $B(x)=A(wx)$，则 $S(B,m,k)=w^k S(A,\lfloor \dfrac{m}{w} \rfloor,k)$。

• 若 $B(x)=\dfrac{1}{1-x} A(x)$，则（$B_t$ 为伯努利数）：

$$\begin{aligned} S(B,m,k) &=\sum\limits_{i=0}^m i^k b_i\\ &=\sum\limits_{i=0}^m i^k \sum\limits_{j=0}^i a_j\\ &=\sum\limits_{j=0}^m a_j \sum\limits_{i=j}^m i^k\\ &=(\sum\limits_{i=j}^m i^k) \sum\limits_{j=0}^m a_j-\sum\limits_{j=0}^m a_j \sum\limits_{i=0}^{j-1} i^k\\ &=(\sum\limits_{i=j}^m i^k) \sum\limits_{j=0}^m a_j-\sum\limits_{j=0}^m a_j \dfrac{1}{k+1} \sum\limits_{t=0}^k \dbinom{k+1}{t} B_t j^{k+1-t}\\ &=(\sum\limits_{i=j}^m i^k) \sum\limits_{j=0}^m a_j-\sum\limits_{t=0}^k \dfrac{1}{k+1} \dbinom{k+1}{t} B_t \sum\limits_{j=0}^m a_j j^{k+1-t}\\ &=(\sum\limits_{i=j}^m i^k) \sum\limits_{j=0}^m a_j-\sum\limits_{t=0}^k \dfrac{1}{k+1} \dbinom{k+1}{t} B_t S(A,m,k+1-t)\\ \end{aligned}$$

上式的前后部分均可卷积优化至 $O(k \log k)$。

注意到每进行一次第二类操作，最大的 $k$ 就无法维护。故只用维护 $k=0,1,\cdots,n$ 即可。

总时间复杂度 $O(n^2 \log n)$。

*标解有可能更优的 $O(n \log^2 n \log m+n^2)$ 做法。

ABC272Ex Flipping Coins 2 (3700)

ABCEx 科技题

容易发现每个位置的硬币的情况都是一样的，下面考虑计算第 $0$ 个硬币未被翻动的概率。这等价于下面这个问题：

求 $[0,n)$ 的排列 $p_1,p_2,\cdots,p_n$ 的个数，使得恰有偶数个 $i$ 满足 $p_i \leq a_i$。

事实上偶数这个目标根本没用，下面考虑对每个 $k \in [0,n]$ 求出恰有 $k$ 个 $i$ 满足 $p_i \leq a_i$ 的排列数量。

即求 $Ferrers$ 棋盘 $S=F(a_1+1,a_2+1,\cdots,a_n+1)$ 的所有 $k-$命中数 $h_k$。记 $k-$ 棋盘数为 $r_k$，有：

$$r_k(n-k)!=\sum\limits_{i=k}^n h_i \dbinom{i}{k}$$

$$h_k=\sum\limits_{i=k}^n (-1)^{k-i} \dbinom{i}{k} r_i (n-i)!$$

而由下降幂棋盘多项式分解定理，有：

$$\sum\limits_{i=0}^n r_{n-i} x^{\underline{i}}=\prod\limits_{i=1}^n (x+a_i-i+1)$$

采用分治下降幂卷积可以算出 $r_i$，再二项式反演即可得到 $h_i$。

总时间复杂度 $O(n \log^2 n)$。

参考资料： 《2020 年集训队论文 浅谈棋盘模型在计数问题中的应用》- 彭思进

AGC009E Eternal Average (3400)

设操作次数为 $d=\frac{n+m-1}{k-1}$。

把初始的 $n+m$ 个数视为 $n+m$ 个点，每次操作 $k$ 个数就新建一个点作为这 $k$ 个数对应的点的父亲。这样可以将操作对应为一棵 $n+m+d$ 个节点的 $k$ 叉树。

设每个点的权值为其儿子权值的平均值，则最后留下的数 $s$ 即根节点的权值。

也即，设初始的 $m$ 个 $1$ 所对应的编号为 $x_1,x_2,\cdots,x_m$，则 $s=\sum_{i=1}^m k^{-dep_{x_i}}$。

注意到，设初始的 $n$ 个 $0$ 所对应的编号为 $y_1,y_2,\cdots,y_n$，则有：

$$\sum\limits_{i=1}^m k^{-dep_{x_i}}+\sum\limits_{i=1}^n k^{-dep_{y_i}}=1$$

考虑如何判定一个 $s$ 是否可被构造出来：

结论：$s$ 可被构造出来当且仅当存在 $x_1,x_2,\cdots,x_m$ 满足 $\sum_{i=1}^m k^{-dep_{x_i}}=s$ 且存在 $y_1,y_2,\cdots,y_n$ 满足 $\sum_{i=1}^n k^{-dep_{y_i}}=1-s$。

证明：必要性显然。充分性：设 $z_t$ 表示为 $t$ 的 $x_i,y_i$ 个数，只需证可以构造一棵树使得深度为 $i$ 的叶子节点恰有 $z_i$ 个。考虑这样一个算法：

• 由 $d$ 至 $1$ 枚举 $p$，由于 $\sum_{t=1}^p z_t k^{-t}=1$，故 $k \mid z_p$。那么对这 $z_p$ 个点建立 $\frac{z_p}{k}$ 个父亲节点，$z_{p-1} \leftarrow z_{p-1}+\frac{z_p}{k},z_p \leftarrow 0$。

即可得到一棵满足条件的树。证毕。

下面考虑计数。考虑将 $s,1-s$ 看作 $k$ 进制小数，设 $s=\sum_{i=1}^d a_i k^{-i},1-s=\sum_{i=1}^d b_i k^{-i}$，其中 $a_i,b_i \in [0,k)$。那么需要满足：

• $\sum_{i=1}^d a_i=m-t_1 (k-1),t_1 \in \N$。

• $\sum_{i=1}^d b_i=n-t_2 (k-1),t_2 \in \N$。

这是因为每一次进位都会使数位和减少 $(k-1)$。

，则 $\{b_i\}$ 即令所有 $a_i \leftarrow k-1-a_i$，再令 $a_d \leftarrow a_d+1$ 后进位获得的结果，设进位次数为 $t_3$，则：

$$\sum_{i=1}^d b_i=d (k-1)+1-\sum_{i=1}^d a_i-t_3 (k-1)$$

$$n-t_2 (k-1)=(n+m)-m+t_1 (k-1)-t_3 (k-1)$$

$$t_2 (k-1)=(t_3-t_1) (k-1)$$

$$t_2 \geq 0 \Leftrightarrow t_3 \geq t_1$$

故枚举 $t_1 \leq t_3$，统计答案。

记 $A$ 个 $[0,k)$ 中的整数组成的和为 $B$ 的数列数量为 $S(A,B)$，可以用容斥计算：

$$S(A,B)=\sum\limits_{i=0}^A (-1)^i \dbinom{A}{i} \dbinom{B-ik+A-1}{A-1}$$

答案为：

$$Ans=\sum\limits_{t_3=0}^{d-1} \sum\limits_{t_1=0}^{t_3} [S(d-t_3,m-t_1(k-1))-S(d-t_3-1,m-t_1(k-1))]$$

直接暴力计算时间复杂度 $O(d^2\frac{m}{k})=O(\frac{m(n+m)^2}{k^3})$，无法通过。

注意到 $A$ 不超过 $d-1$，$B$ 不超过 $m$。枚举最后一个数是什么，用下式递推：

$$S(A,B)=\sum\limits_{i=0}^{k-1} S(A-1,B-i)$$

于是时间复杂度 $O(d\frac{m}{k}+dmk)=O(m(n+m))$，可以通过。

（可能还有更优的做法？）

ABC279Ex Sum of Prod of Min (3300)

第一次用到五边形数定理

限制条件很多，但观察不出什么性质，不如直接硬上。

对第 $t$ 个位置上填的数设出生成函数：

$$\begin{aligned} F_t(x) &=\sum\limits_{i \geq 0} \min(t,i) x^i\\ &=t(\dfrac{x}{1-x}-\dfrac{x-x^{t+1}}{1-x})+x \dfrac{d}{dx} (\dfrac{x-x^{t+1}}{1-x})\\ &=\dfrac{tx^{t+1}}{1-x}+x \dfrac{1-(t+1)x^t+tx^{t+1}}{(1-x)^2}\\ &=\dfrac{x-x^{t+1}}{(1-x)^2}\\ \end{aligned}$$

于是答案为：

$$\begin{aligned} Ans &=[x^m] \prod\limits_{t=1}^n \dfrac{x-x^{t+1}}{(1-x)^2}\\ &=[x^m] \dfrac{x^n}{(1-x)^{2n}} \prod\limits_{t=1}^n (1-x^t)\\ &=[x^{m-n}] (1-x)^{-2n} \prod\limits_{t=1}^n (1-x^t)\\ \end{aligned}$$

由于 $m-n \leq n$，故：

$$\prod\limits_{t=1}^n (1-x^t) \equiv \prod\limits_{t \geq 1} (1-x^t) \pmod{x^{m-n+1}}$$

由五边形数定理：

$$\begin{aligned} Ans &=[x^{m-n}] \sum\limits_{i \geq 0} \dbinom{2n-1+i}{2n-1} \sum\limits_{k \geq 0} (-1)^k x^{k(3k \pm 1)/2}\\ &=\sum\limits_{k \geq 0} (-1)^k \dbinom{2n-1+m-n-(k(3k \pm 1)/2)}{2n-1}\\ \end{aligned}$$

模数较小，用卢卡斯定理计算组合数。注意到枚举的项数只有 $O(\sqrt n)$ 项，时间复杂度 $O(\bmod+\sqrt n \log_{\bmod} n)$。

AGC035E Develop (3700)

给每个数建一个点，数 $x$ 向 $x-2$ 与 $x+K$ 连边。那么最后擦去的集合能为 $S$ 当且仅当 $S$ 的导出子图是 DAG。

当 $K$ 为偶数时，奇偶数独立，且 $S$ 合法当且仅当不包含没有奇/偶数中连续的 $K/2+1$ 个数。那么设 $dp_i$ 表示考虑前 $i$ 个数且第 $i$ 个数不选的方案数，有：

$$dp_i=\sum\limits_{j=i-K/2-1}^{i-1} dp_j$$

可以优化到 $O(n)$。

当 $K$ 为奇数时，情况较为复杂。考虑将奇数与偶数列成两列，并令数 $x$ 向数 $(x+k)$ 连边。为方便，记奇数连向偶数的边为 $A$ 型边，偶数连向奇数的边为 $B$ 型边。

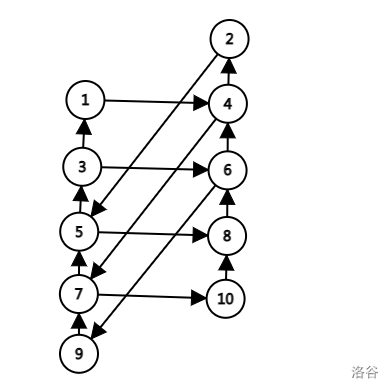
（图来自博客 AGC035E Develop - 淸梣ling）

结论：若 $S$ 的导出子图有环，则必存在一个环仅包含两条连接两侧的边。

证明：取环中最靠下的一条 $A$ 型边 $(u,v)$。设 $u$ 向下延申到 $x$，$v$ 向上延伸到 $y$，$x,y$ 分别与 $x',y'$ 通过 $B$ 型边连接。

• 若 $y \leq x'$，则 $(x,u,v,,x')$ 已经成环。

• 若 $y > x'$，则如图所示。设 $y$ 向上延申到 $z$。由前提假设，$z \leq u$，那么 $(y',u,v,y)$ 已经成环。

故证毕。

而所有这样的环长均为 $K+2$，于是 $S$ 的导出子图无环当且仅当不存在一条从左侧延伸到右侧的长为 $K+2$ 的链。

接下来考虑计数。设 $dp_{i,j,k}$ 表示从上到下考虑前 $i$ 层节点，从第 $i$ 层右侧点延申的链长为 $j$，从第 $i$ 层左侧点延伸到右侧的链长为 $k$。转移：

• 两侧都不选：两边的链都断掉。

$$f_{i-1,j,k} \rightarrow f_{i,0,0}$$

• 选左侧，不选右侧：右侧的链断掉，左侧（若有链）链长加一。

$$f_{i-1,j,k} \rightarrow f_{i,0,k+1}(k>0)$$

$$f_{i-1,j,0} \rightarrow f_{i,0,0}$$

• 选右侧，不选左侧：右侧的链长加一，左侧的链断掉。

$$f_{i-1,j,k} \rightarrow f_{i,j+1,0}$$

• 两侧都选：右侧的链长加一，左侧的链在两种方案中取较大值。

$$f_{i-1,j,k} \rightarrow f_{i,j+1,\max(k+1,j+2)}$$

总时间复杂度 $O(n^2k)$。

ARC154F Dice Game (3600)

为什么省选前要做这个

提供一种不使用生成函数的暴力做法。

考虑扔 $i$ 次已经扔出所有面的概率为 $n! \dfrac{S2(i,n)}{n^i}$，于是期望时间的 $k$ 次方为：

$$s_k =n!\sum\limits_{i \geq 0} (\dfrac{S2(i,n)}{n^i}-\dfrac{S2(i-1,n)}{n^{i-1}}) i^k$$

为了方便计算，取一个趋近于无穷大的整数 $m$，只计算和式中 $i \leq m$ 的部分。

下面用 $\epsilon(m)$ 表示当 $m$ 趋近于无穷大时值趋近于 $0$ 的部分（于是在最终答案的计算中可以忽略）。结论：对于非负整数 $k$ 与实数 $a \in (0,1)$，$\lim\limits_{x \rightarrow \infty} x^k a^x=0$。

$$\begin{aligned} s_k(m) &=n!\sum\limits_{i=0}^m (\dfrac{S2(i,n)}{n^i}-\dfrac{S2(i-1,n)}{n^{i-1}}) i^k\\ &=n! m^k \dfrac{S2(m,n)}{n^m}-n! \sum\limits_{i=0}^{m-1} \dfrac{S2(i,n)}{n^{i}} [(i+1)^k-i^k]\\ \end{aligned}$$

设 $k-1$ 次下降幂多项式 $\sum\limits_{p=0}^{k-1} c_p x^{\underline{p}}=(x+1)^k-x^k$。系数 $c_p$ 稍后再进行推导，下面继续计算上式：

$$\begin{aligned} s_k(m) &=n! m^k \dfrac{S2(m,n)}{n^m}-n! \sum\limits_{p=0}^{k-1} c_p \sum\limits_{i=0}^{m-1} \dfrac{S2(i,n)}{n^{i}} i^{\underline{p}}\\ &=\dfrac{m^k}{n^m} \sum\limits_{t=0}^n (-1)^t \dbinom{n}{t} (n-t)^m -\sum\limits_{p=0}^{k-1} c_p \sum\limits_{i=0}^{m-1} i^{\underline{p}} \sum\limits_{t=0}^n (-1)^t \dbinom{n}{t} \dfrac{(n-t)^i}{n^{i}}\\ &=m^k \sum\limits_{t=0}^n (-1)^t \dbinom{n}{t} (\dfrac{n-t}{n})^m -\sum\limits_{p=0}^{k-1} c_p \sum\limits_{t=0}^n (-1)^t \dbinom{n}{t} \sum\limits_{i=0}^{m-1} (\dfrac{n-t}{n})^i i^{\underline{p}}\\ \end{aligned}$$

第一个和式中，当 $t \neq 0$ 时均趋近于 $0$，故其等于 $m^k+\epsilon(m)$。

第二个和式中，考虑求 $\sum\limits_{i=0}^{m-1} (\dfrac{n-t}{n})^i i^{\underline{p}}$：

• 当 $t=0$ 时，其等于 $\sum\limits_{i=0}^{m-1} i^{\underline{p}}=\dfrac{1}{p+1} m^{\underline{p+1}}$。

• 当 $t \neq 0$ 时，记 $a=\dfrac{n-t}{n}$，$f(x)=\sum\limits_{i=0}^{m-1} a^i x^i=\dfrac{1-(ax)^m}{1-ax}$，所求即：

$$f^{(p)}(1)=p!\dfrac{a^p}{(1-ax)^{p+1}}+\epsilon(m)=p! \dfrac{n}{t} (\dfrac{n-t}{t})^p+\epsilon(m)$$

于是带入得：

$$s_k(m) =m^k+\epsilon(m) -\sum\limits_{p=0}^{k-1} c_p \dfrac{1}{p+1} m^{\underline{p+1}} - \sum\limits_{p=0}^{k-1} c_p \sum\limits_{t=1}^n (-1)^t \dbinom{n}{t} [p! \dfrac{n}{t} (\dfrac{n-t}{t})^p+\epsilon(m)]$$

接下来先推导 $c_t$：

$$\begin{aligned} \sum\limits_{p=0}^{k-1} \dbinom{k}{p} x^p &= \sum\limits_{p=0}^{k-1} \dbinom{k}{p} \sum\limits_{t=0}^p S2(p,t) x^{\underline{t}}\\ &= \sum\limits_{t=0}^{k-1} x^{\underline{t}} \sum\limits_{p=t}^{k-1} \dbinom{k}{p} S2(p,t) \\ \end{aligned}$$

$$\begin{aligned} c_p &=\sum\limits_{t=p}^{k-1} \dbinom{k}{t} S2(t,p)\\ &=\sum\limits_{t=p}^{k} \dbinom{k}{t} S2(t,p) -S2(k,t)\\ &=S2(k+1,t+1)-S2(k,t)\\ &=(t+1) S2(k,t+1)\\ \end{aligned}$$

$$s_k(m) =m^k+\epsilon(m) -\sum\limits_{p=0}^{k-1} S2(k,p+1) m^{\underline{p+1}} - \sum\limits_{p=0}^{k-1} (p+1) S2(k,p+1) \sum\limits_{t=1}^n (-1)^t \dbinom{n}{t} [p! \dfrac{n}{t} (\dfrac{n-t}{t})^p+\epsilon(m)]$$

可以发现关于 $m$ 的部分全部消掉了。

$$s_k=- \sum\limits_{p=0}^{k-1} (p+1)! S2(k,p+1) \sum\limits_{t=1}^n (-1)^t \dbinom{n}{t} \dfrac{n}{t} (\dfrac{n-t}{t})^p$$

$$s_k=\sum\limits_{p=1}^{k} p! S2(k,p) \sum\limits_{t=1}^n (-1)^{t+1} \dbinom{n}{t} \dfrac{n}{t} (\dfrac{n-t}{t})^{p-1}$$

可以分两步计算：

• $$f_p=\sum\limits_{t=1}^n (-1)^{t+1} \dbinom{n}{t} \dfrac{n}{t} (\dfrac{n-t}{t})^{p-1}$$

• $$s_k=\sum\limits_{p=1}^{k} p! S2(k,p) f_p$$

第一步即计算数列 $k$ 次幂和，使用分治乘做到 $O(n \log^2 n+m \log m)$。具体做法可见 P4705 玩游戏.

第二步，将第二类斯特林数拆开：

$$\begin{aligned} s_k &= \sum\limits_{p=1}^{k} f_p \sum\limits_{t=0}^p (-1)^t \dbinom{p}{t} (p-t)^k\\ &= \sum\limits_{p=1}^{k} f_p \sum\limits_{t=0}^p (-1)^{p-t} \dbinom{p}{t} t^k\\ &= \sum\limits_{p=1}^{m} (-1)^p f_p \sum\limits_{t=0}^m (-1)^t \dbinom{p}{t} t^k\\ &= \sum\limits_{t=0}^m (-1)^t t^k \sum\limits_{p=1}^{m} (-1)^p \dbinom{p}{t} f_p \\ \end{aligned}$$

同样分两步计算：

• $$g_t=\sum\limits_{p=1}^{m} (-1)^p \dbinom{p}{t} f_p$$

• $$s_k=\sum\limits_{t=0}^m (-1)^t t^k g_t$$

第一步可以直接 NTT 计算，复杂度 $O(m \log m)$。

第二步同样是计算数列 $k$ 次幂和，复杂度 $O(m \log^2 m)$。

综上，总时间复杂度 $O(n \log^2 n+m \log^2 m)$。