浅谈字符串及各种神奇自动机
众所周知,自动机是处理字符串问题的好方法(废话
由于本人还是太弱,本文不涉及严格证明与构建方法,仅帮助感性理解介绍自动机的原理及应用
先将推荐的博客放在这里(建议结合着看):
写在前面:
-
字符串问题时间复杂度大多是线性或者一个 \(log\)
-
本文中用 \(|S|\) 代表字符串 \(S\) 的长度,用 \(S_i\) 表示字符串 \(S\) 的第 \(i\) 位,用 \(pre_i\) 表示第 \(i\) 位前面的前缀,用 \(suf_i\) 表示前 \(i\) 位后面的后缀
-
本文中默认字符集大小为 \(26\) (小写英文字母)
自动机
有限状态自动机(FSM "finite state machine" 或者FSA "finite state automaton" )是为研究有限内存的计算过程和某些语言类而抽象出的一种计算模型。有限状态自动机拥有有限数量的状态,每个状态可以迁移到零个或多个状态,输入字串决定执行哪个状态的迁移。有限状态自动机可以表示为一个有向图。有限状态自动机是自动机理论的研究对象。——百度百科
哇,没啥用……所以别看上面这个了(
自动机大概就是一个图,每一个点代表一个状态
假如我们有一个字符串,就从初始状态开始,一点一点往后走……
没啦
很简单不是吗
AC 自动机
前置芝士:Trie 树
AC 自动机主要用于字符串的匹配
所以……不如先从简单的开始?
KMP
单模式串匹配单文本串
现在有一个模式串 \(S="abaa"\),和一个文本串 \(T="ababac"\) ,问 \(S\) 在 \(T\) 中出现多少次。
暴力匹配,对于 \(T\) 中的每个位置,判断是否是 \(S\) 的起点,\(O(|S| |T|)\)
这……肯定太暴力了
我们来考虑一下匹配的过程
-
第一位,\(S_1=T_1\),配上了
-
第二位,\(S_2=T_2\),配上了
-
第三位,\(S_3=T_3\),配上了
-
第四位,失配了
从第二位开始再来?
不!我们已经知道第一位是 \(a\) ,第二位是 \(b\),第三位是 \(a\) 了!
从第二位开始肯定配不上
从第三位开始才可能配的上
那么从第四位开始,以 \(S_2\) 和 \(T_4\) 继续比较……
时间复杂度是 \(O(|S|+|T|)\)。
咋实现呢?这不是重点,所以就不讲了
AC 自动机
多模式串匹配单文本串
现在有 \(n\) 个模式串 \(S=“aba”,“bc”,“ba”\),和一个文本串 \(T="abcaba"\) ,问每个 \(S\) 在 \(T\) 中出现多少次。
暴力 KMP , \(O(|T|\sum|S|)\)
还是太暴力了……
多个模式串,怎么办呢
自然而然地会想到建 Trie 树
记第 \(i\) 个字符串在 Trie 树上的终止节点是 \(t_i\)
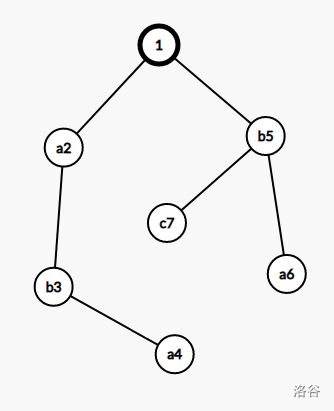
那就是拿文本串在树上跑嘛!
是不是有点自动机的感觉了?
- 在 \(1\) 号节点,有儿子 \(a\),于是来到 \(2\) 号节点
- 在 \(2\) 号节点,有儿子 \(b\),于是来到 \(3\) 号节点
- 在 \(3\) 号节点,没有儿子 \(c\)……
失配了,咋办?
其实这时候还可以从 \(5\) 号节点继续!
因为 \("b"\) 是 \("ab"\) 的后缀
事实上,我们把这个叫做 \(fail\) 指针
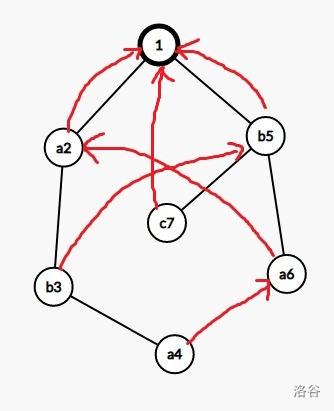
仔细观察一下,显然 \(fail_i\) 代表的字符串是 \(i\) 代表的字符串的一个后缀,而且还是最长的
显然 \(fail\) 指针构成了一棵树(并不显然
当然,到 \(4\) 号节点的时候, \(aba\) 已经匹配上了, \(ba\) 也自然匹配上了
所以到每个节点,都要不停跳 \(fail\) ,将它到 \(1\) 号节点的链上答案都统计一遍
那继续举例
-
在 \(3\) 号节点,没有儿子 \(c\),跳到 \(5\) 号节点
-
在 \(5\) 号节点,有儿子 \(c\),于是来到 \(7\) 号节点,\(ans_{bc}++\)
-
在 \(7\) 号节点,没有儿子 \(a\),于是来到 \(1\) 号节点
-
在 \(1\) 号节点,有儿子 \(a\),于是来到 \(2\) 号节点
-
在 \(2\) 号节点,有儿子 \(b\),于是来到 \(3\) 号节点
-
在 \(3\) 号节点,有儿子 \(a\),于是来到 \(4\) 号节点,\(ans_{aba}++\),\(ans_{ba}++\)
时间复杂度 \(O(|T||S|)\)
还是不太行啊……
到每个节点,都要不停跳 \(fail\) ,将它到 \(1\) 号节点的链上答案都统计一遍
这也太浪费时间了吧……
刚刚不是说 \(fail\) 指针构成了一棵树吗?
那到一个节点就打一个标记,最后再对每个点统计子树标记之和不就行了?
\(O(|T|+\sum|S|)\)
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n;
char s[N*10];
int ch[N][26],nxt[N],in[N];
int cnt,ans[N],mp[N];
queue <int> q;
void findnext(){
q.push(1);
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=0;i<26;i++){
if(ch[x][i]){
int v=ch[x][i];
q.push(v);
if(x==0) nxt[v]=0;
else nxt[v]=ch[nxt[x]][i],in[ch[nxt[x]][i]]++;
}
else ch[x][i]=ch[nxt[x]][i];
}
}
}
int main(){
scanf("%d",&n);
cnt=1;
int maxx=0;
for(int i=0;i<26;i++) ch[0][i]=1;
for(int i=1;i<=n;i++){
scanf("\n%s",s);
int l=strlen(s),x=1;
for(int j=0;j<l;j++){
if(!ch[x][s[j]-'a']) ch[x][s[j]-'a']=++cnt;
x=ch[x][s[j]-'a'];
}
mp[i]=x;//mp是t_i
}
//建 Trie
findnext();
//建 AC 自动机
scanf("\n%s",s);
int l=strlen(s),x=1;
for(int i=0;i<l;i++){
int k=ch[x][s[i]-'a'];
ans[k]++;
x=ch[x][s[i]-'a'];
}
//跑自动机
for(int i=1;i<=cnt;i++) if(!in[i]) q.push(i);
while(!q.empty()){
int u=q.front();
q.pop();
int v=nxt[u];
in[v]--;
ans[v]+=ans[u];
if(!in[v]) q.push(v);
}
//用拓扑排序代替 dfs ,就不用建树了
//当然建树也行
for(int i=1;i<=n;i++) printf("%d\n",ans[mp[i]]);
}
多模式串匹配多文本串
现在有 \(n\) 个串 \(S=“ababa”,“ab”,“bab”,"b","baabab\),\(q\) 个询问第 \(x\) 个字符串在第 \(y\) 个字符串中出现多少次。
现在更难了……
暴力 AC 自动机, \(O((\sum{S})^2)\)
考虑一下询问,其实就是 Trie 树上从 \(1\) 到 \(t_y\) 的每个节点,有多少个能跳 \(fail\) 到 \(t_x\)
刚刚不是说 \(fail\) 指针构成了一棵树吗?
那把 Trie 树上从 \(1\) 到 \(t_y\) 的每个节点权值设为 \(1\) ,就是求 \(t_x\) 的子树和耶
搞出 fail 树的 dfn 就可以用树状数组维护了,很轻松
第二个问题,怎么设权值呢?
其实很简单,在 Trie 树上 dfs ,把根节点到当前节点上的链上的权值全设为 \(1\)
然后查询就好了呀
\(O(\sum S log\sum S)\)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n;
char s[N*10];
int sch[N][26];
int ch[N][26],fa[N],nxt[N],in[N];
int cnt,id,ans[N],mp[N];
queue <int> q;
struct abc{
int x,num;
};
vector <abc> v[N];
struct nod{
int to,nxt;
}e[N*2];
int head[N],cntt;
void add(int u,int v){
e[++cntt].to=v;
e[cntt].nxt=head[u];
head[u]=cntt;
}
void findnext(){
q.push(1);
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=0;i<26;i++){
if(ch[x][i]){
int v=ch[x][i];
q.push(v);
if(x==0) nxt[v]=0;
else nxt[v]=ch[nxt[x]][i],
add(ch[nxt[x]][i],v),add(v,ch[nxt[x]][i]);
}
else ch[x][i]=ch[nxt[x]][i];
}
}
}
int dfin[N],dfout[N],idd;
void dfs(int u,int fa){
dfin[u]=++idd;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa) continue;
dfs(v,u);
}
dfout[u]=idd;
}
int c[N];
int lowbit(int x){
return x & (-x);
}
void modify(int x,int k){
while(x<N) c[x]+=k,x+=lowbit(x);
}
int query(int x){
int ans=0;
while(x) ans+=c[x],x-=lowbit(x);
return ans;
}
int query2(int x){
return query(dfout[x])-query(dfin[x]-1);
}
void dfss(int u,int fa){
modify(dfin[u],1);
for(int i=0;i<v[u].size();i++){
int x=v[u][i].x,num=v[u][i].num;
ans[num]=query2(x);
}
for(int i=0;i<26;i++){
int v=sch[u][i];
if(v==fa || !v) continue;
dfss(v,u);
}
modify(dfin[u],-1);
}
int main(){
cnt=1;
for(int i=0;i<26;i++) ch[0][i]=1;
scanf("%s",s+1);
int l=strlen(s+1);
int x=1;
for(int i=1;i<=l;i++){
if(s[i]=='P') mp[++id]=x;
else{
if(s[i]=='B') x=fa[x];
else{
if(!ch[x][s[i]-'a'])
ch[x][s[i]-'a']=++cnt,
sch[x][s[i]-'a']=cnt,
fa[cnt]=x;
x=ch[x][s[i]-'a'];
}
}
}
//建 Trie
findnext();
dfs(1,0);
cin>>n;
for(int i=1;i<=n;i++){
int x,y;
scanf("%d%d",&x,&y);
v[mp[y]].push_back((abc){mp[x],i});
}
//存每个节点的询问
dfss(1,0);
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
}
AC 自动机 DP
咕了,后补
后缀自动机(SAM)
AC 自动机只能解决匹配之类的问题
如果我们想把一个字符串的所有子串拎出来操作(比如不同子串个数)怎么办呢?
有一个很巧妙的思路:
任意一个子串都是某个后缀的前缀
所以其实只要把后缀都搞出来就好啦
那当然,还是要用最好用的 Trie 树

拿 abbaba 为例:
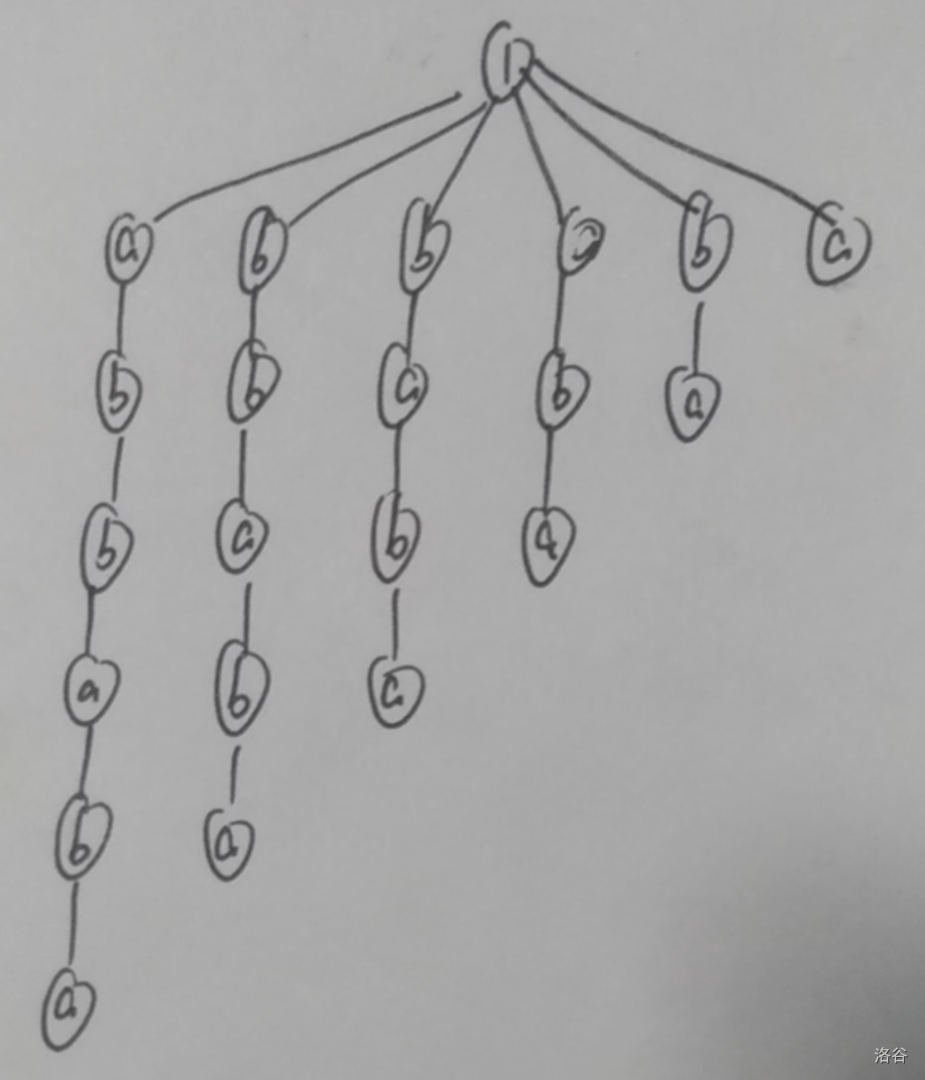
啊,问题来了:这样点数是 \(O(|S|^2)\) 的
但其实,我们可以把它压缩成一个 \(O(|S|)\) 的 DAG :
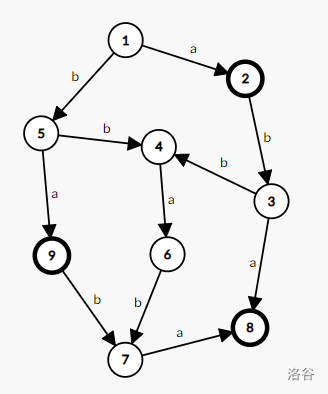
这就是后缀自动机(SAM)
Endpos
怎么把 \(O(|S|^2)\) 个节点变成 \(O(|S|)\) 呢?
有个好东西,叫做 \(Endpos\)
Endpos 实际上是一个集合,表示某个子串在原串中出现时,其最后一个字母在原串中的位置
比如 ba 在 abbaba 中的 Endpos 就是 {4,6} , b 在 abbaba 中的 Endpos 就是 {2,3,5}
事实上, Endpos 有许多奇妙的性质:
考虑在子串前面加一个字母,显然 Endpos 会变少
如果在子串前面加另一个字母,显然 Endpos 也会变少,而且加两种字母得到的 Endpos 互不相交
比如 b 的 Endpos 是 {2,3,5}
加入 a :ab 的 Endpos 是 {2,5}
加入 b :bb 的 Endpos 是 {3}
这……像不像棵树?
Parent 树
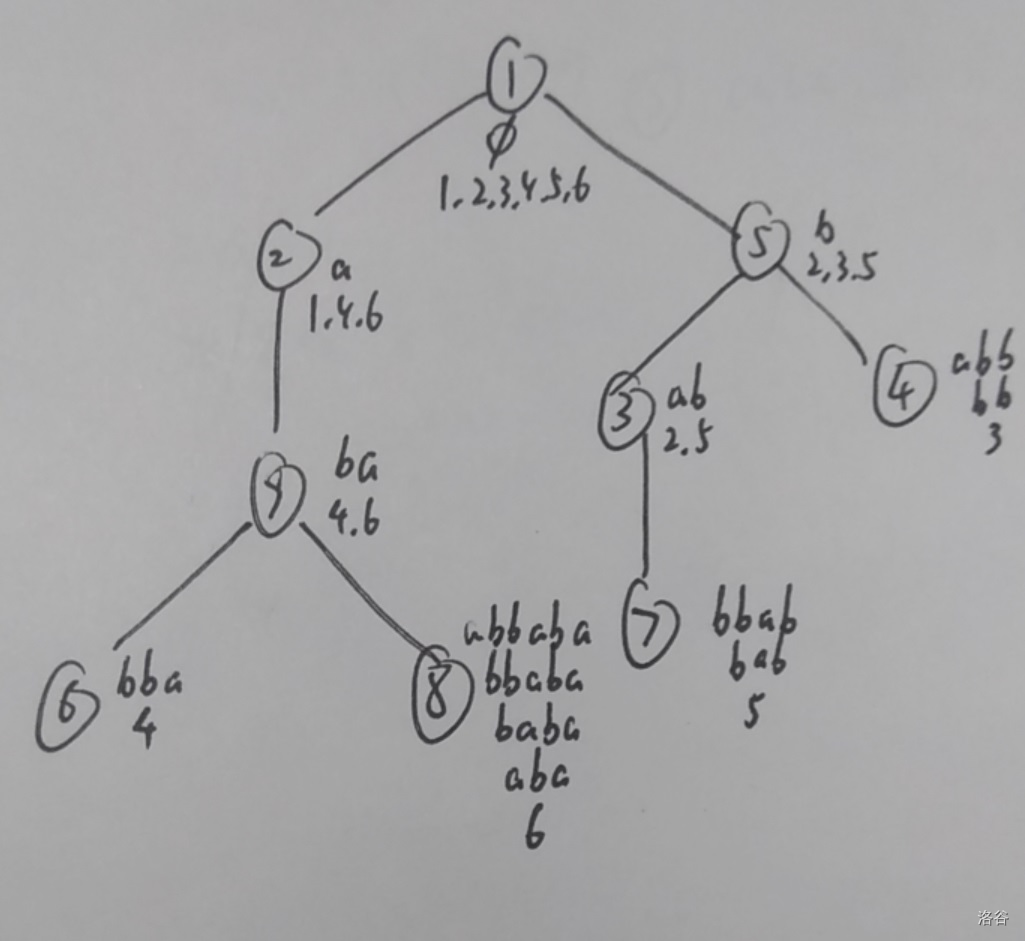
这棵树也有名字,叫做 Parent 树
每个节点叫做一个状态,它包含许多子串,这些子串的 Endpos 是相同的
不妨把状态 \(k\) 中包含的最长的子串记为 \(longest(k)\) , Endpos 集合大小记为 \(size(k)\)
仔细观察一下,还有很多奇妙的性质:
- \(size(k)=\sum\limits_{v \in son(k)} size(v) +[longest(k) \in pre]\)
发现当 \(longest(k)\) 是前缀的时候,只要加上一个字符,它本身的 Endpos 就被丢掉了,所以要加一
- 每个状态包含的子串一定是 \(longest(k)\) 的后缀,而且还是连续的
后缀自动机
接下来是最劲爆的事情:
Parent 树和后缀自动机的节点时一样的!
不信去对比一下上面的两幅图
构建与实现这里就略过了,只说明一下二者的区别
想学习的话建议这里:史上最通俗的后缀自动机详解——KesdiaelKen
-
Parent 树是在子串前面添加字符
-
SAM 是在子串后面添加字符
而且,通过 SAM 走到一个节点得到的字符串,Endpos 就属于这个节点
还有就是,如果把原串对应的节点在 Parent 树上到根的路径都叫 终止节点 ,那原串的每个后缀都会在终止节点停下
是不是很有用啊?
应用
有了这个强大的自动机,能干啥呢?
首先有两个自动机本身基本的东西需要求出来
求每个节点的 Endpos 集合大小
- \(size(k)=\sum\limits_{v \in son(k)} size(v) +[longest(k) \in pre]\)
在 Parent 树上 dp 就可以力
前缀怎么判断呢?只需要在建自动机时的 case 1 判一下就行了
求每个节点包含的子串个数
- 状态 \(k\) 中最短的子串长度 = 状态 \(fa(k)\) 中最长的子串长度 +1
所以就是 状态 \(k\) 中最长的子串长度 - 状态 \(fa(k)\) 中最长的子串长度
接下来开始正式的运用
字符串匹配
刚才 AC 自动机干的事也可以拿后缀自动机来搞啦
拿文本串跑后缀自动机,停下来的节点包含的子串个数就是答案
(不过空间太大了……还是过不了模板题)
求不同的子串个数
显然就是 每个节点包含的子串个数 之和
求第 \(k\) 小子串
dp 出 \(f_i\) 表示:走到 \(i\) 节点后,还可以走到多少个子串
不同位置算作相同:\(f_i=1+\sum\limits_{e(i,v)\in SAM} f_v\)
不同位置算作不同:\(f_i=len_i-len_{fa_i}+\sum\limits_{e(i,v)\in SAM} f_v\)
然后 dfs 一遍就行了
求最长公共前缀(LCP)
- Parent 树是在子串前面添加字符
所以两个子串的最长公共后缀就是 Parent 树上的最近公共祖先(LCA)
前缀咋办呢?
给反串建 SAM 就行啦
回文自动机(PAM)
除了匹配与子串,字符串问题中还有一类特殊的问题——回文串
回文串:原串与反串相同的字符串
这时候就需要奇妙的回文自动机了
回文自动机的本质却和 SAM 比较类似,是用 \(O(n)\) 的时空表示出所有回文串
不过本质不同的回文串本来就只有 \(O(n)\) 个,就不用什么 Endpos 之类的东西压缩了
结构
回文自动机和 AC 自动机很相似,其实也是树(所以也叫回文树)
不过它其实是由两棵树构成的,一棵树存奇数长度的回文串(根节点为 1 节点),另一棵存偶数长度的回文串(根节点为 0 节点)
同样的,每个节点表示一个回文串
- 特别的,0 号节点表示空串,1 号节点不表示任何串(虚点)
边
每个边都有个字符 \(c\) ,由父亲向子节点的转移相当于在父节点串的两旁同时加上 \(c\)
比如 \(aba\) 向子节点连边 \(a\) 就可以得到 \(aabaa\)
len
就是该节点表示的回文串长度
特别的, 0 号节点的 len 是 0, 1 号节点的 len 是 -1
- 因为转移的时候 len 会加 2 ,len 设为 -1 转移后长度就为 1 了,方便很多
size
该节点表示的回文串在原串中的出现次数
fail
和 AC 自动机很类似
fail 指针指向的是 最长回文后缀
但它的应用并不是拿来匹配,而是像 SAM 那样,通过跳 fail 来处理一些信息
- 特别的,0 号和 1 号节点的 fail 都是 1 号节点
num
该节点表示回文串的回文后缀数量
\(num_i=num_{fail_i}+1\)
trans
(有时候光靠以上的几个信息还不足以解决问题)
该节点表示的回文串的长度不超过其一半的最长回文后缀
例如 ababa ,它的 trans 就指向 a
求解方式和 fail 差不多
具体的构建与实现再次略过
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
struct nodd{
int to,nxt;
}e[N*2];
int head[N*2],cntt;
void add(int u,int v){
e[++cntt].to=v;
e[cntt].nxt=head[u];
head[u]=cntt;
}
struct nod{
int ch[27];
int len,fail,siz,num,trans;
nod(){
memset(ch,0,sizeof(ch));
len=fail=0;
}
}t[N*2];
void dfs(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
dfs(v);
t[u].siz+=t[v].siz;
}
}
char s[N];
int lst=0,cnt=1;
void PAM(int n){
int p=lst;
int c=s[n]-'a';
while(s[n-t[p].len-1]!=s[n]) p=t[p].fail;
if(!t[p].ch[c]){
cnt++;
int q=t[p].fail;
while(s[n-t[q].len-1]!=s[n]) q=t[q].fail;
t[cnt].fail=t[q].ch[c];
t[cnt].len=t[p].len+2;
t[cnt].num=t[t[cnt].fail].num+1;
if(t[cnt].len<=2) t[cnt].trans=t[cnt].fail;
else{
int r=t[p].trans;
while(s[n-t[r].len-1]!=s[n] || t[r].len+2>t[cnt].len/2) r=t[r].fail;
t[cnt].trans=t[r].ch[c];
}
t[p].ch[c]=cnt;
}
lst=t[p].ch[c];
t[lst].siz++;
}
long long ans;
int main(){
scanf("%s",s+1);
int l=strlen(s+1);
t[0].fail=t[1].fail=1;
t[1].len=-1;
for(int i=1;i<=l;i++) PAM(i);
for(int i=0;i<=cnt;i++) if(i!=1) add(t[i].fail,i);
dfs(1);
for(int i=1;i<=cnt;i++) ans=max(ans,1ll*t[i].len*t[i].siz);
cout<<ans;
}
小结
自动机是处理字符串问题的有力工具,形式多样,变化多端,也很锻炼思维
不过需要注意的是:自动机的空间真的不小……

