凸包与动态规划——浅谈斜率优化与 wqs 带权二分
广告
你还在为题目限制太多而放弃吗?
你还在为dp太慢而焦虑吗?
你还在为炸空间而烦恼吗?
来试试凸包斜率优化与 wqs 带权二分吧!
简介
(上面怎么又有广告)
前置芝士你需要知道的:动态规划在转移时,最终转移而来的状态称为决策点
斜率优化与 wqs 带权二分都是利用凸包与切线的概念优化 dp 的工具
但是两者算法几乎完全不同,注意不要搞混
斜率优化是利用决策点的特性通过单调栈直接优化
wqs带权二分是通过二分斜率将限制转化为普通的加权问题
那,我们从凸包开始说起吧
凸包与切线
凸包
凸包,众所周知,就是凸起的小山包
为了偷懒方便,本文所提到的凸包都是开口向下的(即斜率单调递减)
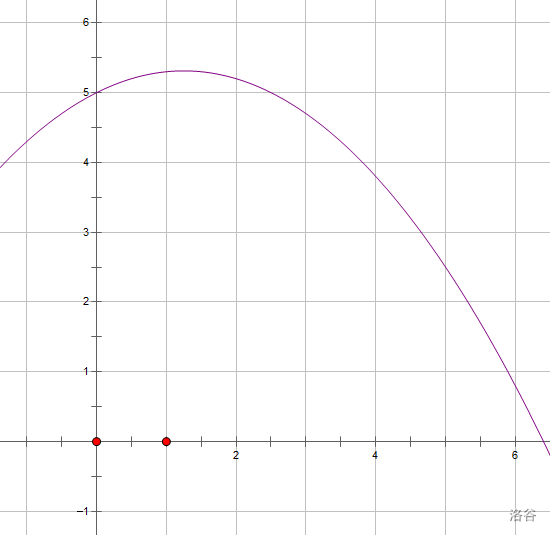
- 在数学上的定义好像是:
若存在, \(f''(x)\) 恒大于或恒小于 \(0\)
也就是 \(f'(x)\) (斜率)有单调性
然而,在 OI 中凸包一般都不是光滑(离散)的
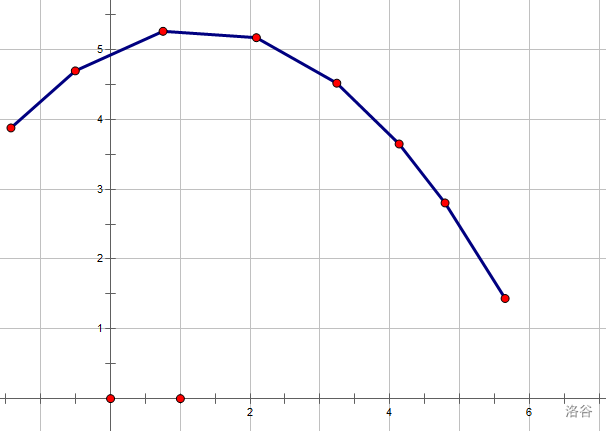
其实定义也是类似的:
经过相邻两点的直线斜率有单调性
- 性质:从凸包中选出一些点连线,仍然是个凸包
证明很显然,斜率有单调性嘛
一次函数
\(y=kx+b\)
-
\(k\) :斜率
-
\(b\) :截距
图像就是根直线
不是这有啥好说的(
切线
凸包 + 一次函数 = 切线!(雾
数学上的定义:与凸包交且只交于一点
数学上一般求过某点的切线,求导即可
可是不光滑的呢?
……好像没办法求
其实我们可以换个方法:求指定斜率为 \(k\) 的切线与切点
过凸包上的每一点作斜率为 \(k\) 的直线试试?

哦?切点的截距是最大的!
(其实原因就是,先把直线放到最上面,一点一点向下移,第一个碰到凸包的就是切点)
那类似的,在不光滑的凸包上也可以这么定义!
-
\(Q\):如果有两个点对应的截距一样怎么办?
-
\(A\):其实就是这两点间的连线的斜率和 \(k\) 相同,其实选哪一个都可以,但实际解题时需要确定好取最左边或最右边的
斜率优化
呃,凸包这种很数学的东西为什么会和动态规划结合在一起啊……
先别管凸包,来道动规题吧
题目
给出序列 \(C_i\) ,可以分成若干组。若将 \(i\) 到 \(j\) 分为一组,则代价为 \((j-i+\sum\limits_{k=i}^j C_k-L)^2\) 。求代价最小值。
动态规划
显然 dp 做
秉承尽量低维的思想,设 \(f_i\) 为 \(i\) 为某组的最后一个时,前 \(i\) 个代价的最小值
转移方程显然
记 \(s_k=\sum\limits_{i=1}^k C_i\)
\(O(n^2)\)
一次函数与凸包
啥,这也能优化?
大佬:你看这个式子,只有 i(相当于常量) 和 j …… 决策点会不会有啥性质?
说干就干,把 j 作为主元试试
记 \(A_j=s_j+j\) ,\(B_i=s_i+i-1-L\)
好家伙,这不就是个关于 \(j\) 的一次函数嘛?!
斜率单调递增(所以是凹的)
而且我们要求的 \(f_i\) 呢,随着 \(b\) 的增大而增大
所以能想到,其实就是在平面直角坐标系上有很多点 \((x,y)=(A_j,f_j+A_j^2)\)
决策点就是过每个点作斜率为 \(k\) 的直线,截距最大的点
想到了啥?
这不就是刚刚说的凸包的切线吗?
但是这又不是凸包……
但其实,如果有三个点形成了凸槽(即斜率不是单调递增的)
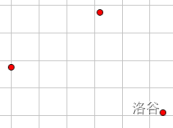
会发现中间那个点无论如何截距都比左边或右边的小
事实上,只有凸包上的点才有可能是决策点
那咋实现呢?
注意到 \(x=A_j=s_j+j\) 单调递增,所以可以一个一个加入
根据上面的理论,加入一个点时,它就能将前面与它形成凹槽的点踢掉
这样就只剩下凸包了!
凸包的斜率单调递增,那拿单调栈维护就可以力
切线与切点
好吧,事情还没有结束
我们要算的是 切点 ,不是 凸包
直接去算显然不太现实
但是我们又发现 \(k=2B_i\) 单调递增
也就是说,切点实际上是一点一点向右移的
然后就很简单了,把单调栈改成单调队列(其实就是增加了从左边删除的操作),每次把尾指针移到切点就可以力
每个点入队/出队至多两次,于是就成功做到了 \(O(n)\) !
附:我们刚刚用到了什么条件?
-
dp是一维的 -
\(k\) 具有单调性
-
\(x\) 单调递增(其实递减可能也行?)
-
\(b\) 与 \(f_i\) 相关
代码
贼短
#include<bits/stdc++.h>
using namespace std;
const long long N=5e4+5,INF=1e18;
long long n,L;
long long a[N],s[N],f[N];
long long q[N],h,t;//队列,尾指针,头指针
double cal(long long l,long long r){
long long xl=l+s[l],xr=r+s[r];
long long yl=f[l]+xl*xl,yr=f[r]+xr*xr;
return 1.0*(yl-yr)/(xl-xr);
}//计算斜率
int main(){
cin>>n>>L;
for(long long i=1;i<=n;i++) cin>>a[i],s[i]=s[i-1]+a[i];
memset(f,0x7f,sizeof(f));
f[0]=0;
h=1,t=1,q[1]=0;
for(long long i=1;i<=n;i++){
long long k=2*(i-1+s[i]-L);//斜率
while(h<t && cal(q[h],q[h+1])<k) h++;//尾指针移到切点
long long j=q[h];//决策点
f[i]=f[j]+(i-j-1+s[i]-s[j]-L)*(i-j-1+s[i]-s[j]-L);//转移
while(h<t && cal(q[t-1],q[t])>cal(q[t],i)) t--;//头指针维护凸包
q[++t]=i;
}
cout<<f[n];
}
练习
二维的 dp ,还要求输出方案
不过本质还是一维 dp 套上斜率优化
(后面还会有其他练习的,所以这里只放一题)
wqs 带权二分
哇,好高大上的名字(其实我觉得叫“斜率二分”更好
虽然同是用凸包优化 dp ,但它与斜率优化截然不同(所以忘掉斜率优化吧)
还记得二项式反演吗?
- 【广告时间】如果你不知道的话可以来看看浅谈二项式反演与容斥
有时候问题中会出现恰好 \(k\) 个的限制,通过二项式反演(或者容斥)可以转化成钦定有 \(k\) 个的问题
wqs带权二分的作用其实和这个很像,只不过不是容斥:
有时候问题中会出现恰好 \(k\) 个的限制,通过 wqs 带权二分可以转化为 没有限制,但是每使用一次就多 \(w\) 的代价 的问题
不懂吗?没关系,往下看吧
题目
你要抓神奇宝贝! 现在一共有 \(n\) 只神奇宝贝。 你有 \(a\) 个『宝贝球』和 \(b\) 个『超级球』,其抓到第 \(i\) 只神奇宝贝的概率分别是 \(p_i\) 和 \(q_i\) ,每种球不能在同一只神奇宝贝上使用多次。求最优策略下,抓到神奇宝贝的总个数期望最大值,保留五位小数。
\(n \leq 10^5\)
动态规划
设 \(f_{i,j,k}\) 为前 \(i\) 个神奇宝贝,用了 \(j\) 个宝贝球和 \(k\) 个神奇球的最大期望值
转移方程显然
\(O(n^3)\)
凸包
这个显然没办法斜率优化了,因为不存在决策点的说法
不过 \(f_{n,j,k}\) 在每行和每列上都是有凸性的
什么,为啥?这里插入两个证明凸性的好方法
-
凸性的证明方法:
-
1.感性理解
-
2.打表找规律(建议)
-
据极不完全统计,第二种方法的正确率可达 100% (雾)
好,不妨把 \(f_{n,a,k}\) 看成一个关于 \(k\) 的函数
那么函数图像就是一个上凸包

我们想求的是 \(f_{n,a,b}\),可是不能直接 \(O(n^3)\) 求……
有一个很巧妙的想法:
通过切线来算出 \(f_{n,a,b}\)
啥意思呢?
还是确定一个斜率 \(k\) ,来算切点
显然 \(k\) 越大,切点就越小
那我们二分 \(k\) ,每次算出切点,不就可以把过 \(b\) 的切线算出来了?
现在只需考虑确定 \(k\) 时怎么算出切点的横坐标与纵坐标
假设切线是 \(y=kx+b\)
刚刚也说过了,切点的 \(b\) 是最大的
\(b=y-kx\)
好,还记得 \(x\) 和 \(y\) 的意义吗?
\(x\) 是使用超级球的个数, \(y\) 是最大期望值
那不就相当于不限制使用超级球的个数,但是使用一个就有 \(k\) 的代价,求最大值(即 \(b\) )与取最大值时使用超级球的个数(即 \(x\) )吗?
当然,\(y=kx+b\) 也求得出来
\(O(n^2)\) dp 即可
还有一个二分呢,假设二分的总数量为 \(V\) (通常是斜率的范围除以精度,这里就是 \(\frac{1}{0.0001}=10000\))
(注意:实际做题时通常将精度开得小一点)
总时间复杂度为 \(O(n^2logV)\)
二分套二分
到这里其实你已经学会 wqs 带权二分力
但是这道题还过不去……
其实既然超级球能把限制去掉,为啥宝贝球不行呢?
一样的道理,在上面的基础上再套一层二分宝贝球的斜率
现在最终要处理的问题就是:
没有限制,但是使用宝贝球和超级球分别有 \(k1\) 和 \(k2\) 的代价,求最大值与取最大值时使用两种球的个数
啊这,这不直接贪心就行?
总时间复杂度为 \(O(nlog^2V)\)
细节
还有点麻烦的小问题
如果有多个点对应的截距一样怎么办?
其实就是这多点共线且连线的斜率和 \(k\) 相同,其实选哪一个都可以,但实际解题时需要确定好取最左边或最右边的
代码里写的是确定最左边的
也就是贪心时尽量不用
最后统计答案的时候乘上的就是二分的左指针
为啥要这样呢?
其实如果要求的点在多点共线中间的话是二分不到的,只能二分到最左边的点
但是就算没有二分到,斜率一定是多点共线的斜率,算出来的答案还是一样的
代码
#include<bits/stdc++.h>
using namespace std;
const int N=2200;
const double eps=1e-6;
int n,a,b;
double p[N],q[N];
double ua,ub,tot;
void check(double a,double b){
ua=ub=tot=0;
for(int i=1;i<=n;i++){
double maxx=0;
int cnta=0,cntb=0;
if(maxx<p[i]-a-eps) maxx=p[i]-a,cnta=1,cntb=0;
if(maxx<q[i]-b-eps) maxx=q[i]-b,cnta=0,cntb=1;
if(maxx<1-(1-p[i])*(1-q[i])-a-b-eps)
maxx=1-(1-p[i])*(1-q[i])-a-b,cnta=1,cntb=1;
ua+=cnta,ub+=cntb;
tot+=maxx;
}
}
int main(){
cin>>n>>a>>b;
for(int i=1;i<=n;i++) cin>>p[i];
for(int i=1;i<=n;i++) cin>>q[i];
double la=0,ra=1,lb,rb;
//外层二分
while(la+eps<ra){
double mida=(la+ra)/2;
lb=0,rb=1;
//内层二分
while(lb+eps<rb){
double midb=(lb+rb)/2;
check(mida,midb);
if(ub>=b) lb=midb;//说明切点偏右,斜率小了
else rb=midb;
if(ub==b) break;//如果切点二分到了b直接退出
}
if(ua>=a) la=mida;
else ra=mida;
if(ua==a) break;//如果切点二分到了a直接退出
}
cout<<tot+la*a+lb*b;
}
练习
没有单独是 wqs 带权二分的练习……
所以来点套娃题!
wqs 带权二分套斜率优化


 浙公网安备 33010602011771号
浙公网安备 33010602011771号