Coppersmith's Method

CopperSmith's Method

Coppersmith算法在ctf的密码学问题中应用越来越广泛，但少有人深究其原理，本文将介绍Coppersmith方法基本原理，所对应的格子构造与格基规约方法，调整Coppersmith求解上界的方法。
注：因blog渲染的原因，本文采用截图的方式展现大部分公式推导内容
本文检索目录：

Reference

https://www.math.auckland.ac.nz/~sgal018/crypto-book/ch19.pdf

Definition

Example

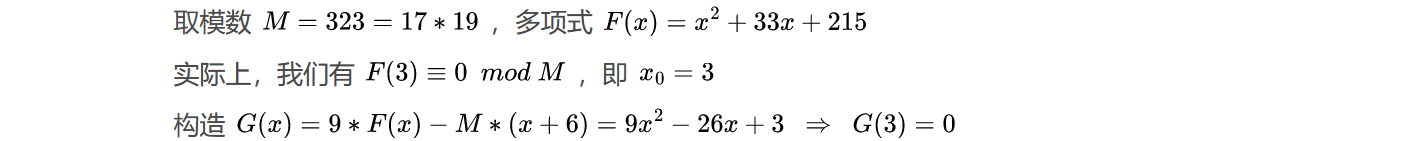
Howgrave-Graham

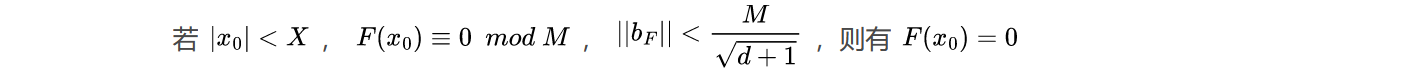
Proof

这波推导梦回高二MOer的日子////

How to Find G(x)

Example

Coppersmith's Method

Coppersmith

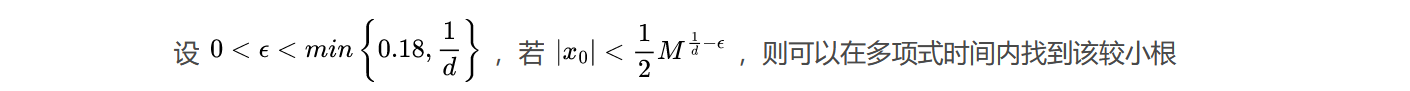
Proof

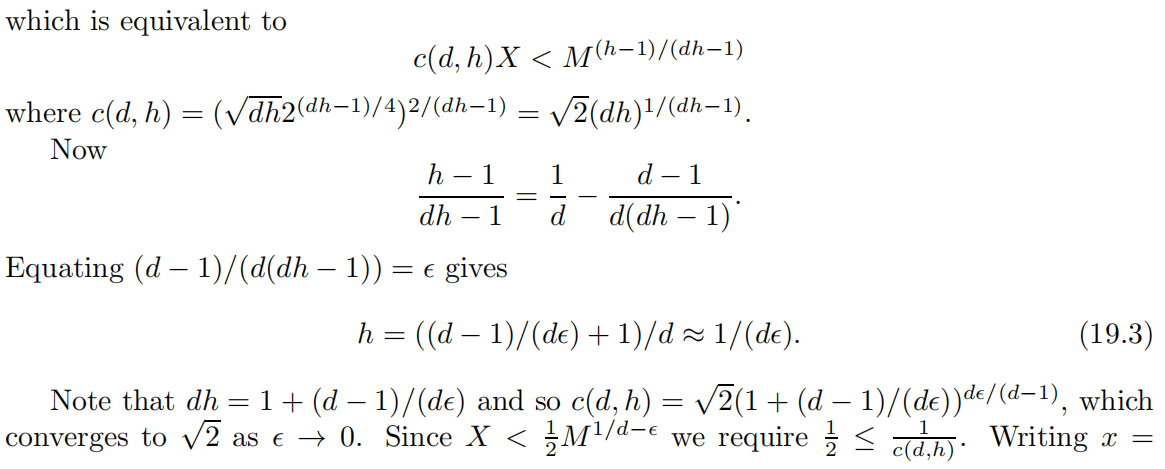
Coding

在实际运用过程中，我们往往使用sagemath中封装好的small_root函数，但部分题目会卡small_root函数的上界，即该函数计算得到的X上界小于求解未知量x0，这时需要我们调整参数，下面用github上开源的一段代码展示调整参数的过程：

def matrix_overview(B, bound):
    for ii in range(B.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(B.dimensions()[1]):
            a += '0' if B[ii,jj] == 0 else 'X'
            a += ' '
        if B[ii, ii] >= bound:
            a += '~'
        print (a)
def coppersmith(pol, modulus, beta, h, t, X):
    # 计算矩阵维度
    n = d * h + t
    # 将多项式转到整数环上
    polZ = pol.change_ring(ZZ)
    x = polZ.parent().gen()
    # 构造上文所述lattice，polZ(x * X) 就是环上的多项式f(X * x)
    g = []
    for i in range(h):
        for j in range(d):
            g.append((x * X)**j * modulus**(h - i) * polZ(x * X)**i)
    for i in range(t):
        g.append((x * X)**i * polZ(x * X)**h)
    # 构造格B
    B = Matrix(ZZ, n)
    for i in range(n):
        for j in range(i+1):
            B[i, j] = g[i][j]
    # 展示格的样式
    matrix_overview(B, modulus^h)
    # LLL
    B = B.LLL()
    # 将最短向量转化为多项式，并且去除相应的X 
    new_pol = 0
    for i in range(n):
        new_pol += x**i * B[0, i] / X**i
    # 解方程
    potential_roots = new_pol.roots()
    # 检查根
    roots = []
    for root in potential_roots:
        if root[0].is_integer():
            result = polZ(ZZ(root[0]))
            if gcd(modulus, result) >= modulus^beta:
                print("p: ",(gcd(modulus, result)))
                roots.append(ZZ(root[0]))
    return roots
N = 
ZmodN = Zmod(N)
P.<x> = PolynomialRing(ZmodN)
pbar = 
f = pbar + x
beta = 0.4
d = f.degree()
epsilon = beta / 7
h = ceil(beta**2 / (d * epsilon))
t = floor(d * h * ((1/beta) - 1))
X = ceil(N**((beta**2/d) - epsilon)) 
roots = coppersmith(f, N, beta, h, t, X)

可以看到：

X = ceil(N**((beta**2/d) - epsilon)) 

Example

可以参考我的另一篇文章，“2023hgame-week3-RSA大冒险2”一题进行参数调整的尝试（还没发出来，等2.7hgame结束发）

Ending

以下内容待更新完善：
1.二元及多元coppersmith原理（大概会另开一篇文章）
2.Some Applications of Coppersmith’s method，这部分可以去原文翻，理解难度不大，也都是大家最常见的板题了，这里就没写（
3.相关函数源码解析，比如这里本来想拿small_root的源码来讲调参，但是咕咕咕了，尽快补一下（主要是想在发hgame crypto wp之前更出来
4.好多国际赛上出现过的有意思的coppersmith构造（或者也可以说是Lattice的构造）会陆续更到这里