2023 hgame crypto wp 全
做了今年hgame的题目,ak crypto的同时也从题目中学到了不少,贴一份所有密码方向题目的wp。
Week 1
RSA | 100pts
根据题目描述,用factorb分解n,在这里用的factorb在线api:
http://factordb.com/api?query=
exp:
from Crypto.Util.number import *
import gmpy2
import requests
def queryFactors(n):
s=[]
url="http://factordb.com/api?query="+str(n)
r = requests.get(url)
factors=r.json()['factors']
for f in factors:
for i in range(f[1]):
s.append(int(f[0]))
return s
c=110674792674017748243232351185896019660434718342001686906527789876264976328686134101972125493938434992787002915562500475480693297360867681000092725583284616353543422388489208114545007138606543678040798651836027433383282177081034151589935024292017207209056829250152219183518400364871109559825679273502274955582
n=135127138348299757374196447062640858416920350098320099993115949719051354213545596643216739555453946196078110834726375475981791223069451364024181952818056802089567064926510294124594174478123216516600368334763849206942942824711531334239106807454086389211139153023662266125937481669520771879355089997671125020789
e=65537
p=queryFactors(n)[0]
q=n//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(long_to_bytes(m))

Be Stream | 100pts
def stream(i):
if i==0:
return key[0]
elif i==1:
return key[1]
else:
return (stream(i-2)*7 + stream(i-1)*4)
这里流密码的生成器是一个二阶线性递推数列,利用数列中的项进行对明文的异或加密操作,暴力递归求解每一项时间复杂度显然是不够的
注意到对明文的异或是在mod 256意义下进行的,于是可以将该数列放在mod 256意义下考虑,而二阶线性递推数列在模意义下具有周期性,本题经验证得到周期为64,于是得到flag
exp:
key = [int.from_bytes(b"Be water", 'big'), int.from_bytes(b"my friend", 'big')]
enc= b''#data
stream=[]
stream.append(key[0]%256)
stream.append(key[1]%256)
for i in range(2,64):
stream.append((stream[i-2]*7 + stream[i-1]*4)%256)
flag=b""
for i in range(len(enc)):
water=stream[((i//2)**6)%64]
flag += bytes([(water ^ enc[i])])
print(flag)

另外在处理二阶线性递推的问题时,往往还会采用矩阵快速幂进行加速,出题人给出的官方wp也用到了这样的方法
enc = b''#data
key = [int.from_bytes(b"Be water", 'big'), int.from_bytes(b"my friend", 'big')]
def mul(a, b):
c = [[0, 0], [0, 0]]
for i in range(2):
for j in range(2):
for k in range(2):
c[i][j] += (a[i][k] * b[k][j]) % 256
c[i][j] %= 256
return c
def power(n):
if n==1: return key[1] % 256
if n==0: return key[0] % 256
res = [[1, 0], [0, 1]]
A = [[4, 7], [1, 0]]
while n:
if n & 1: res = mul(A, res)
A = mul(A, A)
n >>= 1
return (res[1][0] * key[1] + res[1][1] * key[0]) % 256
flag = b''
for i in range(0, len(enc)):
water = power((i//2)**6)
flag += bytes([water ^ enc[i]])
print(flag)
兔兔的车票 | 100pts
题目中生成了部分noise data,利用三张noise图片对原始图片进行异或加密,实际上是key reuse的想法,把经过noise data混淆后的十六张图片两两异或可以试出来
上述方法基于的原理:
1.生成的noise图片中保留了部分(0,0,0)的数据点,导致异或时没有起到混淆作用
2.两张有实际意义的图片进行异或,可以大致看出图片信息,并不会完全混淆,如下图
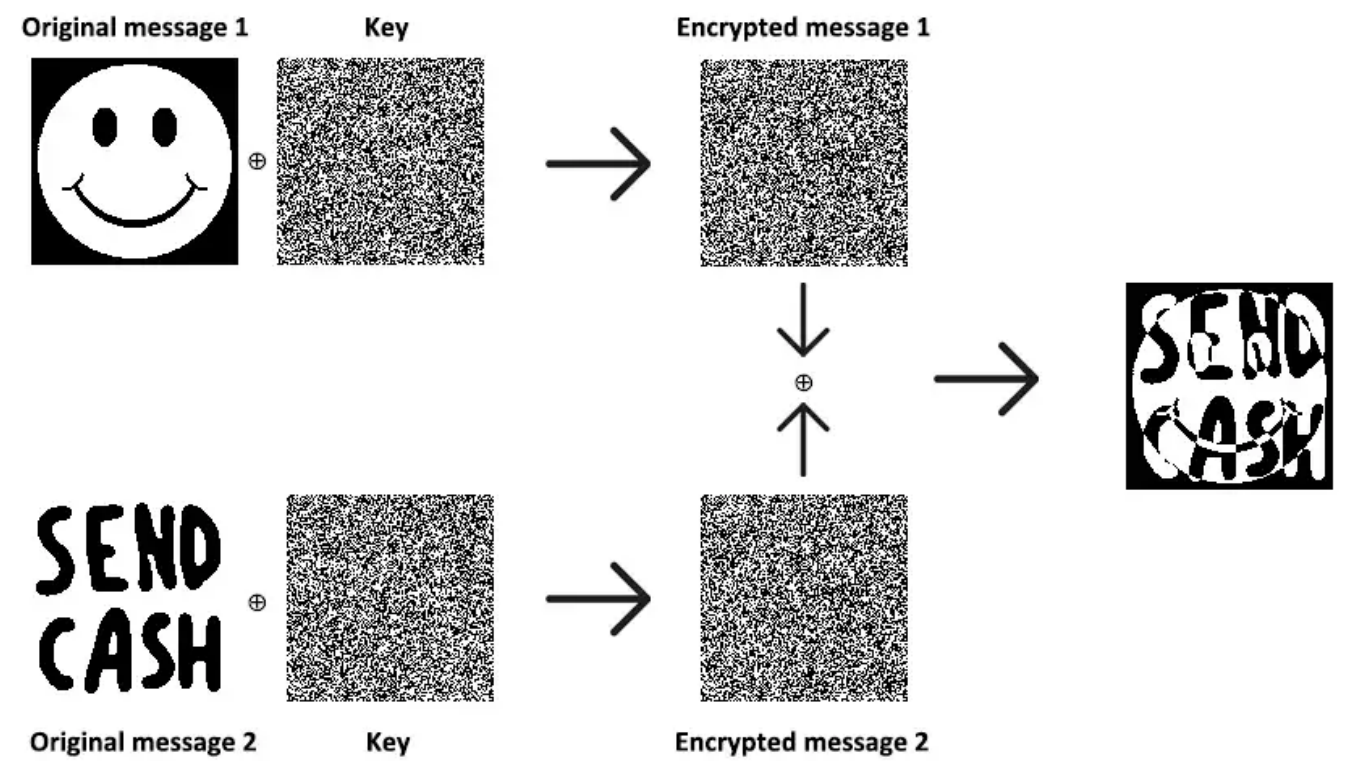
exp:
from PIL import Image, ImageDraw
width=379
height=234
image_path="path\\enc1.png"
img1=Image.open(image_path)
image_path="path\\enc6.png"
img2=Image.open(image_path)
img3 = Image.new("RGB", (width, height))
for i in range(height):
for j in range(width):
p1, p2 = img1.getpixel((j, i)), img2.getpixel((j, i))
img3.putpixel((j, i), tuple([(p1[k] ^ p2[k]) for k in range(3)]))
img3.save('path\\0.png')

神秘的电话 | 100pts
这题套娃了没啥意思,手解morse,得到
0223E_PRIIBLY__HONWA_JMGH_FGKCQAOQTMFR
根据提示,倒序后再解18层的栅栏,得到
rmocfhm_wo_ybipe2023_ril_hnajg_katfqqg
凭感觉像是维吉尼亚,稍微手试结合爆破得到密钥vidar,从而得到flag
week2
包里有什么 | 200pts
经典的背包密码问题,a数组是2为公比的等比数列,符合超递增形式,利用w混淆a数组得到数组b,m为模数
题目给出b[0],已知a[0],可求w
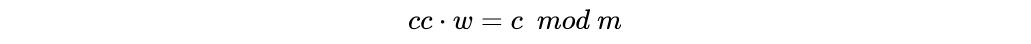
在mod m意义下对c乘w的逆元可以恢复通过用a数组进行背包加密的密文cc,从而利用a数组的超递增性质得到flag
exp:
from Crypto.Util.number import *
import gmpy2
m = 1528637222531038332958694965114330415773896571891017629493424
b0 = 69356606533325456520968776034730214585110536932989313137926
c = 93602062133487361151420753057739397161734651609786598765462162
l=m.bit_length()-2
#w=(b0+m)//2
w=b0//2
a = [2 << i for i in range(l)]
b = [w * i % m for i in a]
assert b[0]==b0
cc=(c*gmpy2.invert(w,m))%m
flag=""
for i in range(len(a)-1,-1, -1):
if cc >= a[i]:
cc -= a[i]
flag+="1"
else:
flag+="0"
flag=flag[::-1]
print(long_to_bytes(int(flag,2)))

也可以求w之后得到b,利用LLL算法进行规约得到flag,但利用LLL算法解背包密码是有约束条件的,并不能对所有情况适用,不能算是本问题的最优解法
Rabin | 150pts
Rabin的板题
exp:
from Crypto.Util.number import *
import gmpy2
e=2
p=65428327184555679690730137432886407240184329534772421373193521144693375074983
q=98570810268705084987524975482323456006480531917292601799256241458681800554123
c=0x4e072f435cbffbd3520a283b3944ac988b98fb19e723d1bd02ad7e58d9f01b26d622edea5ee538b2f603d5bf785b0427de27ad5c76c656dbd9435d3a4a7cf556
n=p*q
a,inv_q ,inv_p= gmpy2.gcdext(q,p)
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
a = (inv_p * p * mq + inv_q * q * mp) % n
b = n - int(a)
c = (inv_p * p * mq - inv_q * q * mp) % n
d = n - int(c)
for i in(a,b,c,d):
print(long_to_bytes(i))

RSA大冒险1 | 200pts
level1:
把p当作模数,RSA中针对明文m较小的常规解法
level2:
def encrypt(self):
m_ = bytes_to_long(self.m)
c = pow(m_ ,self.e, self.p*self.q)
self.q = getPrime(512)
return hex(c)
每次调用encrypt进行加密的时候,会更新q的值,但p的值始终不变,产生了后门漏洞,分析清楚了就是常规的RSA模不互素的板子
level3:
e=3低指数攻击的板子
level4:
def encrypt(self):
m_ = bytes_to_long(self.m)
c = pow(m_, self.e, self.p*self.q)
self.e = getPrime(17)
return hex(c)
每次调用encrypt更新公钥e的值不更新p q,共模攻击的板子
exp:
from Crypto.Util.number import *
import gmpy2
#level1
n=361067668573234937895991468059126957309979597456638107518559509053801374729041826137407865616458091
e=65537
p=283512251808796606274360612102827230673
c=0x59f3320c32623159430da5f90aeb570c113b8773b190269405a57682da80541fd0a137545f9924fac5
phi=p-1
d=gmpy2.invert(e,phi)
m=pow(c,d,p)
print(long_to_bytes(m))
#m<n_But_also_m<p
#level2
num1=51714374014784626103389830324623745659758993696818466586014210858366422589570962326044934205165918356339002759574360310601646796554589261089973724419748591357516363775394363541872361180983687867285327133570976393450434372893591590304184278633127463257220213248050866258191414660072916311978916360257899176269
num2=78196272419906767037902832849004105232756023123277232046319587647595140446895325078900581644916520119933600043244420093307315612825163702610998235549248103079987514827335240153615251940195733209944058117702322811676907822899379157063913023209806857080156813524890681666184681309091756341694731879686951138779
c=0x2efe7c797fe9a3485abd4e6c5020f1a0037e0765b363bb3d857bdf41955ff50225fb87568b885fbfe3a79215afd79f4e5eb3adb1ea2d981a0bba1c2401c8db6aa8a0afb72115240dd02e8a79db70bb96b1c9d3fa1acbd66d20aa0308fcb7e814a8714b0ec0f50d7c8ee3e88433f1d7e3204cd64eb1672829f8d4af7ed9a89647
e=65537
p=GCD(num1,num2)
n=num1
phi=p-1
d=gmpy2.invert(e,phi)
m=pow(c,d,p)
print(long_to_bytes(m))
#make_all_modulus_independent
#level3
n=95956427905848709110790455827730781859758109105059149423798771136301462430886494550451263147653782416592902380881006366962525095344162802236463218784261545406669496659045343242247652612436969313296341862158360642994537918335689393284271914642479655859203315571729535683775913838294618830103890837529279728977
e=3
c=0xfec61958cefda3eb5f709faa0282bffaded0a323fe1ef370e05ed3744a2e53b55bdd43e9594427c35514505f26e4691ba86c6dcff6d29d69110b15b9f84b0d8eb9ea7c03aaf24fa957314b89febf46a615f81ec031b12fe725f91af9d269873a69748
temp=gmpy2.iroot(c,3)[0]
print(long_to_bytes(temp))
#encrypt_exponent_should_be_bigger
#level4
e1=69317
c1=0x9ced9e743f5a8e6d7b492001a607464f166cbf01869aa2348462681a54ef620e7698c8c8bfcd3e69357959fc561fb567b7bfd110103fc4a9749b44b2d8d92d16a8d3febf064d62c22b0c86e0915b54697e657e509e370a7233a6fe16cc08d1f5423a9f109b2e3d24cdece14b37a768bd09e3d4b73b724aaeb75c85633c443c72
n=132737573094397166200928323625376462448848709444893383097753580817921870674064012914464680073446196954339074738165979967268640670655884248726027366288498282161714749783486609569598319765091144131157441483840208937402381051309052892634969923866469069795545874253572601030174066186475561988582476654384721746937
e2=113723
c2=0x714d0aff617f24ded351530f942ca8dc9e9c2f5466c24c494245ddf625720fe4e1d34c7fc3c9e99d6ac1d21eb0d2daba111de9e13c778eed4fe6cf03d2951b27a46b0b9b931bb416b1d3bbca76cdd0225f7187075e81e49e9ccc713cb2bb39ced501276ea3c03363eecaade4445fad88216f5e11b812121f963582f79d339bad
gcd, s, t = gmpy2.gcdext(e1, e2)
if s < 0:
s = -s
c1 = gmpy2.invert(c1, n)
if t < 0:
t = -t
c2 = gmpy2.invert(c2, n)
plain = (gmpy2.powmod(c1, s, n) * gmpy2.powmod(c2, t, n)) % n
print(long_to_bytes(plain))
#never_uese_same_modulus
零元购年货商店 | 250pts
审一下源码
func Encrypt(u string) (string, error) {
block, err := aes.NewCipher(key)
if err != nil {
return "", err
}
plainText := []byte(u)
blockMode := cipher.NewCTR(block, iv)
cipherText := make([]byte, len(plainText))
blockMode.XORKeyStream(cipherText, plainText)
return base64.StdEncoding.EncodeToString(cipherText), nil
}
func Decrypt(cipherText string) (string, error) {
decodeData, err := base64.StdEncoding.DecodeString(cipherText)
if err != nil {
return "", errors.New("invalid base64")
}
block, err := aes.NewCipher(key)
blockMode := cipher.NewCTR(block, iv)
plainText := make([]byte, len(decodeData))
blockMode.XORKeyStream(plainText, decodeData)
return string(plainText), nil
}
利用CTR模式进行了AES加密,CTR模式密文改动某一字节,明文只有对应字节改动,尝试得到将cookie第十三位ascii+=1,对应用户名第一位ascii+=3,因此先将用户名设置为Ridar-Tu
cookie:
ESJsI22Q3vTqbTR5am7kjg7Qwm3RlmQbZA2VFfx4OfQu1veLIrevOSpWQ1MQiszz8eKa%2FaF%2FazDChg%3D%3D
修改为:
ESJsI22Q3vTqaTR5am7kjg7Qwm3RlmQbZA2VFfx4OfQu1veLIrevOSpWQ1MQiszz8eKa%2FaF%2FazDChg%3D%3D
因为没有go环境所以只能这样枚举试一试,实际上应该直接调用题目中的encrypt和decrypt函数求解,只需要满足传入用户名为八位字符即可

官方exp:
package main
import (
"encoding/base64"
"fmt"
"net/url"
)
func main() {
var encodedToken = ""
token, _ := url.QueryUnescape(encodedToken)
decodeData, _ := base64.StdEncoding.DecodeString(token)
decodeData[9] ^= 'a' ^ 'V'
decodeData[10] ^= 'a' ^ 'i'
decodeData[11] ^= 'a' ^ 'd'
decodeData[12] ^= 'a' ^ 'a'
decodeData[13] ^= 'a' ^ 'r'
decodeData[14] ^= 'a' ^ '-'
decodeData[15] ^= 'a' ^ 'T'
decodeData[16] ^= 'a' ^ 'u'
attackData := base64.StdEncoding.EncodeToString(decodeData)
fmt.Println(token)
fmt.Println(attackData)
attackToken := url.QueryEscape(attackData)
fmt.Println(attackToken)
}
week3
ezDH | 300pts
离散对数可以求B,从而得到shared secret,然后简单推一下式子:
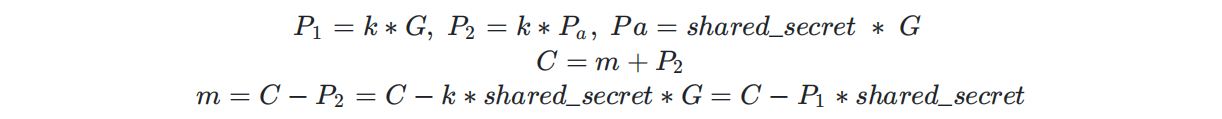
exp:
from Crypto.Util.number import *
N=0x2be227c3c0e997310bc6dad4ccfeec793dca4359aef966217a88a27da31ffbcd6bb271780d8ba89e3cf202904efde03c59fef3e362b12e5af5afe8431cde31888211d72cc1a00f7c92cb6adb17ca909c3b84fcad66ac3be724fbcbe13d83bbd3ad50c41a79fcdf04c251be61c0749ea497e65e408dac4bbcb3148db4ad9ca0aa4ee032f2a4d6e6482093aa7133e5b1800001
g=2
B=0x1889c9c65147470fdb3ad3cf305dc3461d1553ee2ce645586cf018624fc7d8e566e04d416e684c0c379d5819734fd4a09d80add1b3310d76f42fcb1e2f5aac6bcdd285589b3c2620342deffb73464209130adbd3a444b253fc648b40f0acec7493adcb3be3ee3d71a00a2b121c65b06769aada82cd1432a6270e84f7350cd61dddc17fe14de54ab436f41b9c9a0430510dde
#Bob_secret=sympy.discrete_log(N,B,g)
#print(B_s)
Bob_secret=523395080617584542626887374797915530377197776414307699064494325754883865689240606662282052952769155869279302851357127396057956141700522707614969003724858649469855458912748021620773222294584347455737042066389082761054791847391943575954645806724433924897674867376454396257875249718213145700160788809038411884417511593659507
A=0x22888b5ac1e2f490c55d0891f39aab63f74ea689aa3da3e8fd32c1cd774f7ca79538833e9348aebfc8eba16e850bbb94c35641c2e7e7e8cb76032ad068a83742dbc0a1ad3f3bef19f8ae6553f39d8771d43e5f2fcb986bd72459456d073e70d5be4d79ce5f10f76edea01492f11b807ebff0faf6819d62a8e972084e1ed5dd6e0152df2b0477a42246bbaa04389abf639833
p=6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
a=-3
b=1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
E = EllipticCurve(GF(p), [a, b])
shared_secret=210079986310539059026469300720655426951919393335485123618687987029746658763798439576376646226161293006261472023436870446704160814487044427272498126726277523426054334489402918696632471053566567964288295442264373353184045686758631952518445700562724692050307270259376021103356466045824174058551054535796277627154836626119222585862131679625673279898703654
P1=E((2032638959575737798553734238953177065671021112450002471824225734491735604600003028491729131445734432442510201955977472408728415227018746467250107080483073647, 3510147080793750133751646930018687527128938175786714269902604502700248948154299853980250781583789623838631244520649113071664767897964611902120411142027848868))
c=E(6670373437344180404127983821482178149374116817544688094986412631575854021385459676854475335068369698875988135009698187255523501841013430892133371577987480522, 6648964426034677304189862902917458328845484047818707598329079806732346274848955747700716101983207165347315916182076928764076602008846695049181874187707051395)
P2=shared_secret*P1
m=(c-P2)[0]
print(long_to_bytes(m))

至于为什么起手想到了离散对数解B,N的结尾是00001,N-1应该比较光滑,自然可以联想到Pohlig-Hellman algorithm解DLP
ezBlock | 350pts
近期应该会更一篇差分的文章,更完了贴到这里,这里就先简单说下思路
经过了四轮S-box,每一次已知经过S-box混淆前后的值,就有一定概率得到对应的key,感觉这题设计成可以选择明文的交互,主动探索良好的差分性质会更理想
exp:
m_list = [hex(i * 0x1111)[2:].rjust(4, '0') for i in range(16)]
c_list = [28590, 33943, 30267, 5412, 11529, 3089, 46924, 59533, 12915, 37743, 64090, 53680, 18933, 49378, 23512, 44742]
c_list = [hex(i)[2:].rjust(4, '0') for i in c_list]
s_box = {0: 0x6, 1: 0x4, 2: 0xc, 3: 0x5, 4: 0x0, 5: 0x7, 6: 0x2, 7: 0xe, 8: 0x1, 9: 0xf, 10: 0x3, 11: 0xd, 12: 0x8, 13: 0xa, 14: 0x9, 15: 0xb}
ans = []
for k in range(4):
t = {}
for i in range(16):
t[int(m_list[i][k], 16)] = int(c_list[i][k], 16)
for a in range(16):
for b in range(16):
for c in range(16):
for d in range(16):
for e in range(16):
key = [a,b,c,d,e]
for i in range(16):
m = i
for j in range(4):
m = m ^ key[j]
m = s_box[m]
m = m ^ key[4]
if m != t[i]:
break
elif i==15:
ans.append(key)
print(ans)
key = [0, 0, 0, 0, 0]
for k in ans:
key = [(key[i]*16+k[i]) for i in range(5)]
print([hex(i) for i in key])
flag = 'hgame{' + hex(key[0])[2:] + '_' + hex(key[1])[2:] + '_' + hex(key[2])[2:] + '_' + hex(key[3])[2:] + '_' + hex(key[4])[2:] + '}'
print(flag)
#[[4, 15, 4, 4, 13], [15, 4, 15, 5, 8], [4, 9, 9, 7, 13], [2, 3, 2, 0, 5]]
#['0x4f42', '0xf493', '0x4f92', '0x4570', '0xd8d5']

RSA大冒险2 | 350pts
level1:
Boneh_Durfee's attack板子
level2:
yafu可以分解
看了官方wp,出题人想出一个费马分解,那yafu可以分解n就不奇怪了
level3:
指向我的另一篇文章:https://www.cnblogs.com/App1eTree/p/coppersmith.html
coppersmith的板子,但是被卡了上界,需要手动调下参数
这里只给出level3利用small roots方法解根的exp:
def coppersmith(pol, modulus, beta, h, t, X):
n = d * h + t
polZ = pol.change_ring(ZZ)
x = polZ.parent().gen()
g = []
for i in range(h):
for j in range(d):
g.append((x * X)**j * modulus**(h - i) * polZ(x * X)**i)
for i in range(t):
g.append((x * X)**i * polZ(x * X)**h)
B = Matrix(ZZ, n)
for i in range(n):
for j in range(i+1):
B[i, j] = g[i][j]
B = B.LLL()
new_pol = 0
for i in range(n):
new_pol += x**i * B[0, i] / X**i
potential_roots = new_pol.roots()
roots = []
for root in potential_roots:
if root[0].is_integer():
result = polZ(ZZ(root[0]))
if gcd(modulus, result) >= modulus^beta:
print("p: ",(gcd(modulus, result)))
roots.append(ZZ(root[0]))
return roots
N = 131435096190932476282107019932753538842822700854000789960859541290365971093411528417224106949167098928833908993920820537191845190683132521684195137876258992862198519678667815269992895368819967417416360582282152133401991348142208574505338629119903776681479509250804953601559034849627028222835444168985167733627
ZmodN = Zmod(N)
P.<x> = PolynomialRing(ZmodN)
leak = 884164308941646697376000124313396231277143112153939022790874440209793278332165
#f = pbar + x
for i in range(132,2**9):
print(i)
pbar=((leak<<9)+i)<<244
f=pbar + x
beta = 0.50
d = f.degree()
epsilon = beta / 45
h = ceil(beta**2 / (d * epsilon))
t = floor(d * h * ((1/beta) - 1))
X = ceil(N**((beta**2/d) - epsilon))
roots = coppersmith(f, N, beta, h, t, X)
print(roots)
#b'now_you_know_how_to_use_coppersmith'
week4
LLLCG | 50pts
最开始的附件少打了一个括号,用后一个数据除掉前一个数据就可以了,好像RCTF也有一样的非预期哈哈
ECRSA | 400pts
RSA毕竟是基于大整数分解困难的,但是这里给出了p q,只是定义在椭圆曲线上,故对于私钥d的定义变为
d=inverse(e, order)
其中order是圆锥曲线的阶,再就是需要在F(p) F(q)上分别求出明文,利用中国剩余定理CRT进行合并得到最终的flag
exp:
from sage.all import *
from sage.all_cmdline import *
from Crypto.Util.number import *
p=115192265954802311941399019598810724669437369433680905425676691661793518967453
q=109900879774346908739236130854229171067533592200824652124389936543716603840487
n = 1265973137163332340636107173548074387094288440751164714475805591193132153433
a = 3457301624586139606837804088262299224575469302815229087413111295501888448568
b = 1032821371338209482066820365696715669963814382548975103442891640397173555138
e = 11415307674045871669
ciphertext = b''
Ep = EllipticCurve(Zmod(p), [a, b])
Eq = EllipticCurve(Zmod(q), [a, b])
cx = bytes_to_long(ciphertext)
cp = Ep.lift_x(Integer(cx))
cq = Eq.lift_x(Integer(cx))
dp = inverse(e, Ep.order())
dq = inverse(e, Eq.order())
mp = (dp * cp).xy()[0]
mq = (dq * cq).xy()[0]
flag = CRT_list([ZZ(mp), ZZ(mq)], [p, q])
print(long_to_bytes(int(flag)))
LLLCG Revenge | 350pts
HNP问题,LCG、DSA等算法都可以作为oracle产生相邻项参数之间线性递推的效果
这里n是360bit,r最大是340bit,至少泄露20bit的MSB,起手构造矩阵进行LLL,过后会把之前blog关于HNP的文章迁移过来,到时候在这里放链接
exp:
from Crypto.Util.number import *
t = 39
n = 2348542582773833227889480596789337027375682548908319870707290971532209025114608443463698998384768703031935081
# Load data
s=[data]
# Calculate A & B
A = []
B = []
for i in range(len(s)-1):
A.append(ZZ((-1*s[i])%n))
for i in range(1,len(s)):
B.append(ZZ(s[i]))
# Construct Lattice
K = 2^340 # ki < 2^340
X = n * identity_matrix(QQ, t) # t * t
Z = matrix(QQ, [0] * t + [K/n] + [0]).transpose() # t+1 column
Z2 = matrix(QQ, [0] * (t+1) + [K]).transpose() # t+2 column
Y = block_matrix([[X],[matrix(QQ, A)], [matrix(QQ, B)]]) # (t+2) * t
Y = block_matrix([[Y, Z, Z2]])
# Find short vector
Y = Y.LLL()
a=n*Y[1][39]/2**340
print(long_to_bytes(a))

Good luck for hgame 2024



 浙公网安备 33010602011771号
浙公网安备 33010602011771号