Paillier CryptoSystem

Paillier CryptoSystem

Introduce

一种较新的非对称加密模式，一种支持加法同态的公钥密码系统。

Key Generation

常见加密方式有两种，下面给出参数选取方式

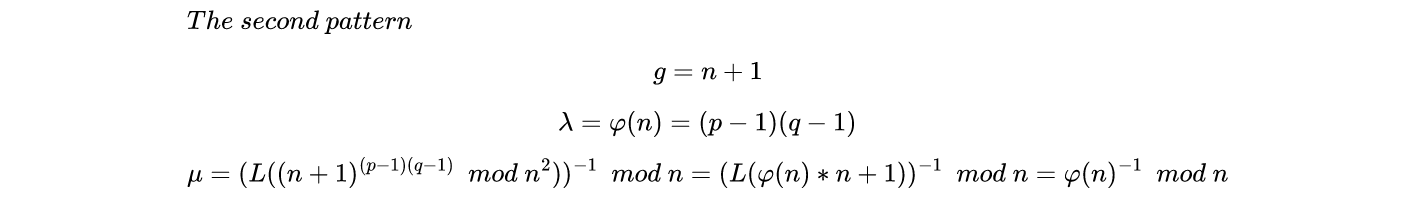
Encryption

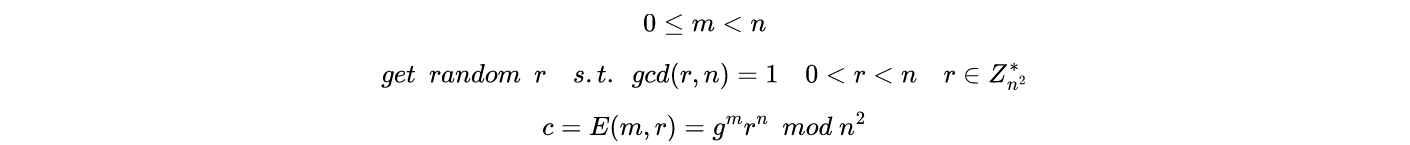
Decryption

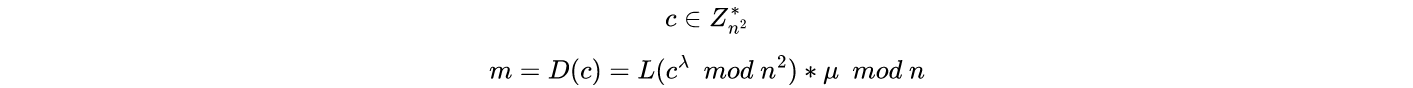
Proof

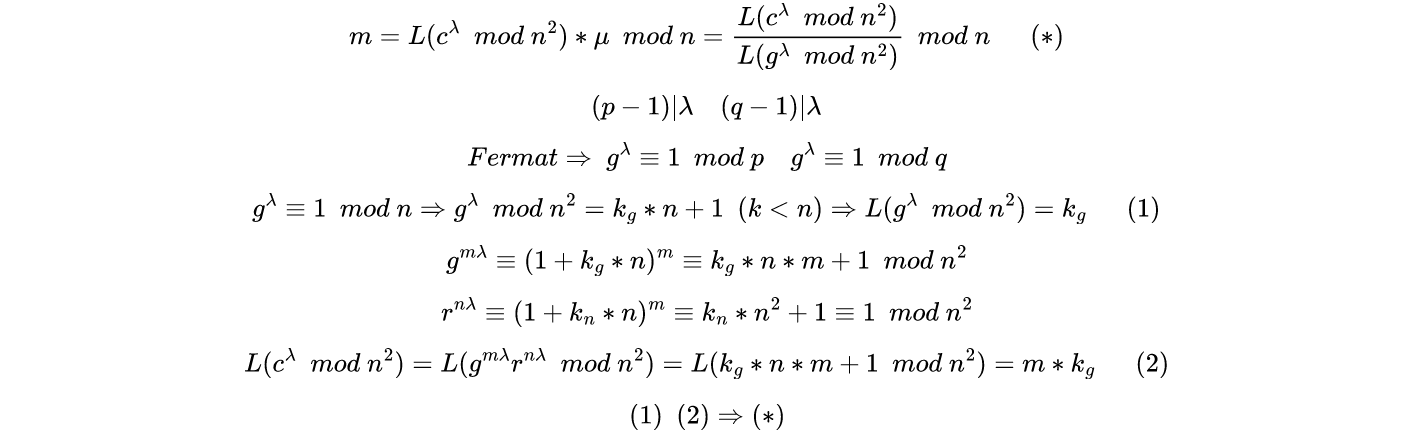
Homomorphic properties

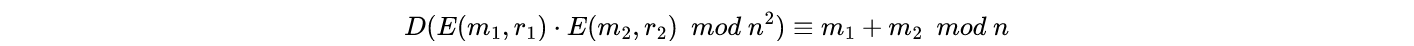
Problem

DASCTF Apr not RSA

from Crypto.Util.number import getPrime as bytes_to_long
from secret import flag,p,q
from sympy import isprime,nextprime
import random
m=bytes_to_long(flag)
n=p*q
g=n+1
r=random.randint(1,n)
c=(pow(g,m,n*n)*pow(r,n,n*n))%(n*n)
print "c=%d"%(c)
print "n=%d"%(n)

第二类加密方式
exp：

from Crypto.Util.number import long_to_bytes,inverse
from sympy import nextprime
from gmpy2 import iroot
def L(x,n):
    return (x-1)/n
c=
n=
#factor(n)
a = iroot(n,2)[0]
p = nextprime(a)
q = n//p
assert p*q == n
Lambda = (p-1)*(q-1)
miu = inverse(Lambda,n)
m = (L(pow(c,Lambda,n**2),n)*miu)%n
print long_to_bytes(m)

2022BytesCTF compare

from Crypto.Util.number import getPrime, getRandomNBitInteger, inverse
from fractions import Fraction
from gmpy2 import lcm
import re

N = 512
safe_expr = re.compile(r'^([-+*/0-9.~%^&()=|<>]|and|or|not|MSG)+$')

def encode(m, n, g):
    r = getRandomNBitInteger(N)
    c = pow(g, m, n*n) * pow(r, n, n*n) % (n*n)
    return c

def decode(c, n, l, u):
    return int(Fraction(pow(c, l, n * n) - 1, n) * u % n)

def round(expr):
    p = getPrime(N)
    q = getPrime(N)

    n = p * q
    g = getRandomNBitInteger(N)
    print('n =', n)
    print('g =', g)

    a = getRandomNBitInteger(N)
    b = getRandomNBitInteger(N)

    print('a =', encode(a, n, g))
    print('b =', encode(b, n, g))

    msg = int(input("msg = "))

    l = int(lcm(p - 1, q - 1))
    u = inverse(Fraction(pow(g, l, n * n) - 1, n), n)

    return (a > b) is bool(eval(expr, None, {'MSG': decode(msg, n, l, u)}))

def main():
    expr = input('Hello, Give me your expr: ')
    expr = re.sub(r'\s', '', expr)

    if safe_expr.match(expr) is None:
        raise Exception('Hacker?')

    for i in range(100):
        print('Round:', i)
        try:
            assert round(expr)
        except:
            print('You lost.')
            break
    else:
        print('Congratulations!')
        print(open('/flag').read())

if __name__ == '__main__':
    main()

from pwn import *
from Crypto.Util.number import *
import gmpy2
p=remote('ip')
p.recvuntil(b'Hello, Give me your expr: ')
p.sendline(b'MSG < 2**512')
for i in range(100):
    p.recvuntil(b'n = ')
    n=int(p.recvuntil(b'\n')[:-1].decode())
    mod=n*n
    p.recvuntil(b'a =')
    a=int(p.recvuntil(b'\n')[:-1].decode())
    p.recvuntil(b'b =')
    b=int(p.recvuntil(b'\n')[:-1].decode())
    msg=a*gmpy2.invert(b,mod)%mod
    p.sendline(str(msg).encode())
    print(i)
p.interactive()