「IOI2018」Highway 高速公路收费

题目描述：

在日本，城市是用一个高速公路网络连接起来的。这个网络包含 $N$ 个城市和 $M$ 条高速公路。每条高速公路都连接着两个不同的城市。不会有两条高速公路连接相同的两个城市。城市的编号是从 $0$ 到 $N-1$ ，高速公路的编号则是从 $0$ 到 $M-1$ 。每条高速公路都可以双向行驶。你可以从任何一个城市出发，通过这些高速公路到达其他任何一个城市。

使用每条高速公路都要收费。每条高速公路的收费都会取决于它的交通状况。交通状况或者为顺畅，或者为繁忙。当一条高速公路的交通状况为顺畅时，费用为 $A$ 日元（日本货币），而当交通状况为繁忙时，费用为 $B$ 日元。这里必有 $A<B$ 。注意，$A$ 和 $B$ 的值对你是已知的。

你有一部机器，当给定所有高速公路的交通状况后，它就能计算出在给定的交通状况下，在两个城市 $S$ 和 $T(S≠T)$之间旅行所需要的最小的高速总费用。

然而，这台机器只是一个原型。所以 $S$ 和 $T$ 的值是固定的（即它已经被硬编码到机器中），但是你并不知道它们的值是什么。你的任务就是去找出 $S$ 和 $T$ 的值。为了找出答案，你打算先给机器设定几种交通状况，然后利用它输出的高速费用来推断出 $S$ 和 $T$ 。由于设定高速公路交通状况的代价很大，所以你并不想使用这台机器很多次。

实现细节:

你需要实现下面的过程：

void find_pair(int N, std::vector<int> U, std::vector<int> V, int A, int B)

$N$: 城市的数量。
$U$ 及 $V$ : 长度为 $M$ 的数组，其中 $M$ 为连接城市的高速公路的数量。对于每个 $(0 \leq i \leq M-1)$，高速公路 $i$ 连接城市 $U[i]$ 和 $V[i]$。
$A$: 交通状况顺畅时高速公路的收费。
$B$: 交通状况繁忙时高速公路的收费.

对于每个测试样例，该过程会被调用恰好一次。
注意，$M$ 为数组的长度，可以按照注意事项的相关内容来取得。

过程 $find$_$pair$ 可以调用以下函数:

long long ask(std::vector<int> w)

w 的长度必须为 $M$ 。数组 $w$ 描述高速公路的交通状况。
对于每个 $(0 \leq i \leq M-1)$，$w[i]$ 表示高速公路 $i$ 的交通状况。 $w[i]$ 的值必须为 $0$ 或 $1$ 。
- $w[i] = 0$ 表示高速公路 $i$ 的交通状况为顺畅。
- $w[i] = 1$ 表示高速公路 $i$ 的交通状况为繁忙。
该函数返回的是，在 $w$ 所描述的交通状况下，在城市 $S$ 和 $T$ 之间旅行所需的最少总费用。
该函数最多只能被调用 $100$ 次（对于每个测试样例）。

$find$_$pair$ 应调用以下过程来报告答案 :

void answer(int s, int t)

$s$ 和 $t$ 的值必须为城市 $S$ 和 $T$（两者的先后次序并不重要）。
该过程必须被调用恰好一次。

如果不满足上面的条件，你的程序将被判为 $Wrong Answer$ 。否则，你的程序将被判为
$Accepted$，而你的得分将根据 $ask$ 的调用次数来计算（参见子任务）。

输入格式：

交互库将读取如下格式的输入：

第 $1$ 行：$N$ $M$ $A$ $B$ $S$ $T$
第 $i+2$ 行 $(0 \leq i \leq M-1)$：$U[i]$ $V[i]$

输出格式：

如果你的程序被判为 $Accepted$ ，交互库打印出 $Accepted:$ $q$ ，这里的 $q$ 为函数 $ask$被调用的次数。
如果你的程序被判为 $Wrong Answer$ ，它打印出 $Wrong Answer:$ $MSG$ 。各类 $MSG 的含义如下：

$answered$ $not$ $exactly$ $once$：过程 $answer$ 没有被调用恰好一次。
$w$ $is$ $invalid$：传给函数 $ask$ 的 $w$ 的长度不是 $M$ ，或者某个 $i$ $(0 \leq i \leq M-1)$ 上的 $w[i]$ 既不是 $0$ 也不是 $1$ 。
$more$ $than$ $100$ $calls$ $to$ $ask$：函数 $ask$ 的调用次数超过 $100$ 次。
${s, t}$ $is$ $wrong$：调用 $answer$ 时的 $s$ 和 $t$ 是错的。

样例：

设 $N=4$,$M=4$,$U=[0,0,0,1]$,$V=[1,2,3,2]$,$A=1$,$B=3$,$S=1$ 和 $T=3$ 。评测程序调用 $find$_$pair(4, \{0, 0, 0, 1\}, \{1, 2, 3, 2\}, 1, 3)$ 。

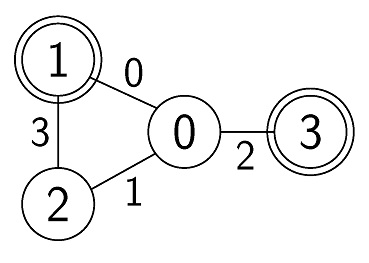
上图中，编号为的 $i$ 边对应高速公路 $i$ 。其中一些对 $ask$ 的可能调用和对应的返回值如下表所示：

\[\begin{matrix} 调用 & & & & & & & & & 返回值 \\ ask(\{0,0,0,0\}) & & & & & & & & & 2 \\ ask(\{0,1,1,0\}) & & & & & & & & & 4 \\ ask(\{1,0,1,0\}) & & & & & & & & & 5 \\ ask(\{1,1,1,1\}) & & & & & & & & & 6 \end{matrix} \]

对于函数调用 $ask(\{0, 0, 0, 0\})$ ，所有高速公路的交通状况均为顺畅，因此每条高速公路的费用都是 $1$ 。从城市 $S=1$ 到城市 $T=3$ 的费用最低的路径就是 $1 \to 0 \to 3$。这条路径的总费用等于 $2$ 。因此，这个函数的返回值就是 $2$ 。

对于一个正确的解答来说，过程 $find$_$pair$ 应调用 $answer(1, 3)$ 或 $answer(3, 1)$。

数据范围与提示：

$2 \leq N \leq 90000$
$1 \leq M \leq 130000$
$1 \leq A \leq B \leq 1000000000$
对于每个$0 \leq i \leq M-1$
- $0 \leq U[i] \leq N-1$
- $0 \leq V[i] \leq N-1$
- $U[i] \neq V[i]$
$(U[i],V[i]) \neq (U[j],V[j])且(U[i],V[i]) \neq (U[j],V[j]) (0<i<j \leq M-1)$
你可以从任何一个城市出发，通过高速公路到达其他任何一个城市。
$0 \leq S \leq N-1$
$0 \leq T \leq N-1$
$S \neq T$
在本题中，评测程序不是适应性的。意思是说，在评测程序开始运行的时候 SSS 和 TTT 就固定下来，而且不依赖于你的程序所做的询问。

子任务：

\[\begin{matrix} 编号 & 分值 & & & & & & & 限制 \\ 1 & 5 & & & & & & & S 或 T 有一个是 0,N \leq 100, M = N-1 \\ 2 & 7 & & & & & & & S 或 T 有一个是 0,M = N-1 \\ 3 & 6 & & & & & & & M=N-1,U[i]=i,V[i]=i+1(0 \leq i \leq M-1) \\ 4 & 33 & & & & & & & M=N-1 \\ 5 & 18 & & & & & & & A=1,B=2 \\ 6 & 31 & & & & & & & 没有附加限制 \\ \end{matrix} \]

假设你的程序被判为 $Accepted$，而且函数 $ask$ 调用了 $X$ 次。你在该测试样例上的得分 $P$ ，取决于对应子任务的编号，其计算如下：

子任务 1 ：$P=5$ 。
子任务 2 ：如果 $X \leq 60$ ，$P=7$ 。否则 $P=0$ 。
子任务 3 ：如果 $X \leq 60$ ，$P=6$ 。否则 $P=0$ 。
子任务 4 ：如果 $X \leq 60$ ，$P=33$ 。否则 $P=0$ 。
子任务 5 ：如果 $X \leq 52$ ，$P=18$ 。否则 $P=0$ 。
子任务 6 ：
- 如果 $X \leq 50$ ，$P=31$ 。
- 如果 $51 \leq X \leq 52$ ，$P=21$ 。
- 如果 $53 \leq X$，$P=0$ 。

注意，你在每个子任务上的得分，等于你在该子任务中所有测试样例上的最低得分。

题解：

一道被机房dalao ~~Dance-Of-Faith~~ A穿了的IOI题。个人认为这个是一道非常好的题目，在做着子任务的时候，慢慢的标算就可以推出来了，做出来之后发现也不是特别毒瘤，做起来也是十分享受的。所以我们怼着子任务一个一个做过去吧。

子任务1：

这个应该不用多讲吧，由于边数最多只有$99$条，并且这是一棵树，所以我们可以先询问一次，得到$S$与$T$的距离之后一条一条边询问过去即可。

子任务2：

这个相比于子任务1不同的地方在于这棵树的边数会有很多，所以并不能一条一条询问过去。于是我们开始想给出了$S$和$T$有一个点在$0$的条件有什么用。首先，我们还是需要询问一次来得到$S$和$T$之间的距离$dist$，然后因为一个点在$0$，那么我们就可以确定另一个点是在以这个点为根的树中深度为$dist$之间的节点中的一个。然后就是很好想了，我们把可能的节点全部都取出来，然后在这些点之中二分。假设当前的区间是$[l,r]$，那么我们将$[l,mid]$之中所有的点到根节点之间的路径全部都设置成$1$，这样，如果得到的回答仍然还是$dist*A$则说明$[l,mid]$区间没有所求的点，继续在$[mid+1,r]$之间二分，否则在$[l,mid]$之间二分，这样就可以得到另一个节点的位置了，最多的询问次数为$log(n)+1=18$次。

子任务3：

这个应该没有什么好讲的吧，就是一条链上二分搞搞就可以了。

子任务4：

这个子任务是最接近正解的一个了吧，题目中只保证这是一颗树。想一想会发现，如果我们两个点的位置都不知道的话，实际上是做不出来的。所以我们尽量的将这个子任务转化成之前的比较简单的子任务。实际上，虽然题目没有保证$S$和$T$中至少一个是$0$，但是我们可以构造出这样的一种情况，即确定了某条边$e=u \to v$是从$S$到$T$之间的一条边，然后把这条边割掉，分成两个树，在以$u$为根的子树中找$S$，以$v$为根的子树中找$T$。这样我们就相当于把这转化成了子任务2了，之后的做法都是一样的。最多的询问次数是$log(m)+2*log(\frac{n}{2})=17+16*2=49$次询问。

子任务5：

这。。就跳过了吧。。虽然并不知道这个子任务到底怎么做，或许有高妙的做法吧，但是我们通过前几个子任务实际上就可以推出标算了。

子任务6：

现在我们要在一个图中考虑这道题目了。实际上，之前的子任务已经提示很多了，既然之前的子任务都是在树中完成的，那么我们就会想到实际上这道题目或许在树中比较容易做一些。于是我们还是考虑把这幅图转化成一棵树，然后按照子任务4的做法就可以完成了。但是我们需要考虑到一点，就是我们如果把这幅图转成树，$S$到$T$的最短花费可能就会改变。实际上，我们只需要找到一条边$e=u \to v$，使得$e$至少在一条从$S$到$T$的最短路上，然后分别一$u$和$v$为根，两边形成两棵$Bfs$树，这样就可以转化成子任务4了。为什么呢？首先我们找到了这样一条边$e$，并且形成了$Bfs$树之后，我们就可以把所有的非树边都染成$B$，这样从$S$到$T$的最少花费的路径一定是在这个树上的。于是我们就相当于强制把这个图转化成了一棵树了。之后和子任务4的做法就是一样的。所以接下来具体的讲一讲如何找到一条这样的边$e$。
首先我们仍然采用二分的方法。假设我们当前二分到了区间$[l,r]$，并且$S$到$T$的最小花费仍然是$dist*A$。然后我们尝试将$[l,mid]$的所有的边染成$B$，如果这样查询之后的最小花费不再是$dist*A$，那么在$[l,mid]$区间中至少有一条边处于从$S$到$T$的最短路上的，于是我们就继续在$[l,mid]$中二分，否则在$[mid+1,r]$中二分。

引用一段来自Dance_Of_Faith的讲解：

但是这里我还是想要讲一下细节上存在的问题，也就是染$A$染$B$交换什么时候会出问题。在树上做的时候完全不会有问题，我前面说了，因为树上的最短路径是唯一的。但图上我们始终坚持保留一条全$A$的路径，也就是让判定条件是$dist*A$，原因很简单，如果不这么做会导致另一条不一定是最短路的路径成为当前染色情况下的带权最短路。
举一个在找$e=u \to v$时的例子，假设$A<<B$，$s$到$t$有两条长为$2,3$的路径，一开始所有边都是$B$：如果我们第一次二分把长度为$3$的路径染为$A$，得到的回答会是$3*A$，也就是走了长度为$3$的路，我们无法从中知道这些染成$A$中的边中是否一定存在最短路上的边。以及在$Bfs$树上二分的时候，如果调换$A,B$的角色，只把树边染成$B$，每次二分的时候把树上的二分范围以外的边染成$A$，问题就会和上个例子类似。实际结果就是询问得到的最短路有可能是从横跨两棵树的边上绕过去的，而并没有经过$u \to v$，因为一个点可能从它的子树中绕出去会更短，具体例子在这里就不做说明了。

最后计算一下最多需要的询问次数：
1.刚开始需要一次询问来得到$dist$。
2.二分得到边$e$，需要$log(m)=17$次。
3.在每棵树上二分，最多需要$2*log(n)=16*2=32$次。

所以这样最多只需要$50$次就可以完成任务，并且这实际上并不会被卡成这样，所以知道算法之后还是比较容易过的。

Code

#include "highway.h"
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
typedef pair<int,int>P;
const int N=1e5+500;
#define fi first
#define se second
#define mk make_pair
std::vector<int>w,T1,T2;
vector<P>G[N];
int disu[N],disv[N],idxu[N],idxv[N];
int n,m,pos;
ll res,dist;

int GetPath() {
  fill(w.begin(),w.end(),0);
  int l=0,r=m-1;
  while(l<r) {
    int mid=(l+r)>>1;
    for(int i=l;i<=mid;i++) w[i]=1;
    if(ask(w)==res) l=mid+1;
    else {
      for(int i=l;i<=mid;i++) w[i]=0;
      r=mid;
    }
  }
  return l;
}

void Bfs(int st,int *dis,int *idx) {
  queue<int>Q;
  while(!Q.empty()) Q.pop();
  for(int i=0;i<n;i++) dis[i]=-1;
  Q.push(st);
  dis[st]=0;
  while(!Q.empty()) {
    int o=Q.front();Q.pop();
    for(auto p:G[o]) {
      int to=p.fi,id=p.se;
      if(dis[to]==-1) {
	dis[to]=dis[o]+1;
	idx[to]=id;
	Q.push(to);
      }
    }
  }
}

int Solve(vector<int>&In,vector<int>&Ot,int *idxIn,int *idxOt) {
  int l=0,r=In.size()-1;
  while(l<r) {
    int mid=(l+r)>>1;
    for(int i=0;i<m;i++) w[i]=1;
    w[pos]=0;
    for(int i=1;i<(int)Ot.size();i++)  w[idxOt[Ot[i]]]=0;
    for(int i=1;i<=mid;i++) w[idxIn[In[i]]]=0;
    ll ret=ask(w);
    if(ret==res) r=mid;
    else l=mid+1;
  }
  return In[l];
}

void find_pair(int N,std::vector<int> U,std::vector<int> V,int A,int B) {
  n=N,m=U.size();
  for(int i=0;i<m;i++) w.push_back(0);
  for(int i=0;i<m;i++) {
    G[U[i]].push_back(mk(V[i],i));
    G[V[i]].push_back(mk(U[i],i));
  }
  res=ask(w);
  dist=res/A;
  pos=GetPath();
  Bfs(U[pos],disu,idxu);
  Bfs(V[pos],disv,idxv);
  for(int i=0;i<n;i++) {
    if(disu[i]<disv[i]) T1.push_back(i);
    if(disv[i]<disu[i]) T2.push_back(i);
  }
  sort(T1.begin(),T1.end(),[](int x,int y) {return disu[x]<disu[y];});
  sort(T2.begin(),T2.end(),[](int x,int y) {return disv[x]<disv[y];});
  int pos1=Solve(T1,T2,idxu,idxv);
  int pos2=Solve(T2,T1,idxv,idxu);
  answer(pos1,pos2);
  return ;
}

posted @ 2018-09-22 16:03 Apocrypha 阅读(837) 评论(0) 编辑收藏举报

刷新页面返回顶部

Apocrypha

「IOI2018」Highway 高速公路收费