317号子任务 CCF 201903-5 Apare_xzc Dijkstra 60分(据说没有AC的)

317号子任务

---

题面：

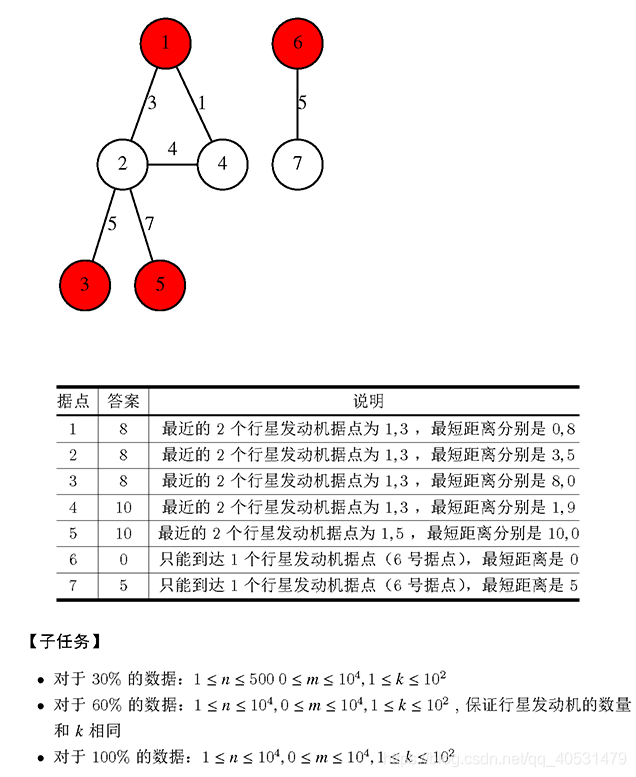
Sample input

7 6 2
1 0 1 0 1 1 0
1 4 1
1 2 3
2 4 4
2 3 5
2 5 7
6 7 5

Sample output

8
8
10
10
0
5

---

据说这题没人100分，最高60…

思路：

1. 存图，我用链式前向星
2. 去重边和自环, 用map<<int,int>int>
3. 因为60%的数据行星发动机据点数<=K<=100, 而n<=10000. 所以我用Dijkstra算法求出每个行星发动机据点到所有点的最短距离。时间复杂度O(Knlog2(n))
   10010000*log2(10000)

---

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4+100;
const int maxm = 2e4+100;
const int INF = 0x3f3f3f3f;
int head[maxn],strong[maxn],tot,n;
struct Node{
	int Next,to,d;
}node[maxm];
void initEdge()
{
	tot = 0;
	memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int d)
{
	node[tot].to = v;
	node[tot].d = d;
	node[tot].Next = head[u];
	head[u] = tot++;
}
map<pair<int,int>,int> mp;
map<pair<int,int>,int>::iterator it;
//strong[i]为 1 的站点是行星发动机据点
//可能是以个不连通的图
//可能有重边和自环
//对于每个点，求距离它K个最近的行星据点到到他的距离之和
struct Point{
	int x,d;//节点X离原点的距离为d
	bool operator < (const Point& rhs)const{
		return d > rhs.d;
	}
	Point(int xx,int dd):x(xx),d(dd){}
};
vector<int> far[maxn];
bool vis[maxn];
int Dis[maxn];
void Dijkstra(int st)
{
	for(int i=1;i<=n;++i)
		vis[i] = false, Dis[i] = INF;
	Dis[st] = 0;
	priority_queue<Point> Q;
	Q.push(Point(st,0));
	while(!Q.empty())
	{
		int id = Q.top().x;
		int dis = Q.top().d;
		Q.pop();
		if(vis[id]) continue;
		vis[id] = true;
		far[id].push_back(dis);
		for(int i=head[id];i!=-1;i=node[i].Next)
		{
			int to = node[i].to;
			int d = node[i].d;
			if(vis[to]) continue;
			if(Dis[to]==-1||Dis[to]>dis+d)
			{
				Dis[to] = dis+d;
				Q.push(Point(to,Dis[to]));
			}
		}
	}
}

int main()
{
	int m,k,u,v,w;
	vector<int> V;
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;++i)
	{
		scanf("%d",strong+i);
		if(strong[i]) V.push_back(i);
	}
	pair<int,int> pii;
	for(int i=0;i<m;++i)
	{
		scanf("%d%d%d",&u,&v,&w);
		if(u==v) continue; //去自环
		if(u>v) swap(u,v);
		pii = make_pair(u,v);
		if(!mp.count(pii))
			mp[pii] = w;
		else if(mp[pii]>w) //去重边
			mp[pii] = w;
	}
	initEdge();
	for(it=mp.begin();it!=mp.end();++it)
	{
		u = it->first.first;
		v = it->first.second;
		w = it->second;
		addedge(u,v,w);
		addedge(v,u,w);
	}
	int len = V.size();
	for(int i=0;i<len;++i)
	{
		Dijkstra(V[i]);
	}
	for(int i=1;i<=n;++i)
	{
		sort(far[i].begin(),far[i].end());
		int ans = 0;
		int sz = far[i].size();
		for(int j=0;j<sz&&j<k;++j)
		{
			ans += far[i][j];
		}
		printf("%d\n",ans);
	}
	return 0;
}

---