BPTT详解

一、基本概念 

RNN前向传播图

    

 

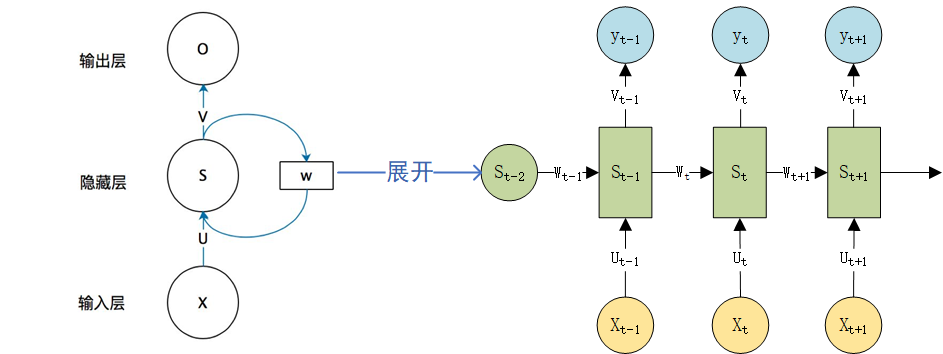
对应的前向传播公式和每个时刻的输出公式

$S_{t}=tanh(UX_t+WS_{t-1})  \qquad \qquad {y_t}'=softmax(VS_t)$

使用交叉熵为损失函数，对应的每个时刻的损失和总的损失。通常将一整个序列（一个句子）作为一个训练实例，所以总的误差就是各个时刻（词）的误差之和。

$ L_t=-y_tlog{y_t}' =-\sum_i y_{t,i}log(y_{t,i}')$

$ L=\sum_t L_t=-\sum_ty_tlog({y_t}') $

将各公式整理如下：

 $

\left{\begin{matrix}
S_{t}=tanh(UX_{t}+WS_{t-1})\\
z_t=VS_t\\
{y_t}'=softmax(z_t)\\
L_t=-y_t log{y_t}'=-\sum_i y_{t,i}log(y_{t,i}') \\
L=\sum_t L_t
\end{matrix}\right.

$

 对各个符号的解释

符号	解释
K	词汇表的大小
T	句子长度
H	隐藏层大小
$z_t$	长度为K的vector
${y_t}$	长度为K的vector,表示真实的标签，一般是one-vector
$y_{t,i}$	对应的第i个词的标签值
${y_t}'$	长度为K的vector,表示预测的向量
$y_{t,i}'$	表示生成的词在是词表的第i个词的概率
$L_t$	当前时刻的损失
$L$	一个句子的损失，由各个时刻的损失求和得到，$L=\sum_t L_t$
$V\in \mathbb{R}^{K \times H}$	隐藏层到输出层的权重
$W\in \mathbb{R}^{H \times K}$	上一个隐藏层状态到当前层的输入的权重
$U\in \mathbb{R}^{H \times H}$	输入的权重

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

二、具体梯度求导

1.对V的导数

$ \frac{\partial L}{\partial V}=\sum_t \frac{\partial L_t}{\partial V}$

$L_t=-y_t log{y_t}'=-\sum_i y_{t,i}log(y_{t,i}')$

$y_{t,i}'=\frac{e^{z_{t,i}}}{\sum_k e^{z_{t,k}}}$

由链式求导法则

$\frac{\partial L_t}{\partial V}=\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial V } \qquad \qquad \frac{\partial L_t}{\partial z_t }=\frac{\partial L_t}{\partial {y_t}' } \frac{\partial {y_t}' }{\partial z_t }  $

其中$\frac{\partial L_t}{\partial {y_t}'} $和$\frac{\partial {z_t}}{\partial V }$的值如下

$\frac{\partial L_t}{\partial {y_t}'} =-\sum_{t,i}\frac{ y_{t,i}}{y_{t,i}'}' $

$\frac{\partial {z_t}}{\partial V }=S_t$

 

$z_t$是一个向量，如果生成的词是第i个词，那么i对应的位置的交叉熵和其他位置的交叉熵是不同的。

1)如果 $i = j$:第i位置的交叉熵

$\frac{\partial y_{t,i}'}{\partial z_{t,i}}=\frac{e^{z_{t,i}} \sum_k e^{z_{t,k}} - e^{z_{t,i}} e^{z_{t,i}}} {({\sum_k e^{z_{t,k}}})^2}=\frac{e^{z_{t,i}}}{\sum_k e^{z_{t,k}}}(1-\frac{e^{z_{t,i}}}{\sum_k e^{z_{t,k}}})=y_{t,i}'(1-y_{t,i}')$

2)如果 $i \neq j$:其他位置的交叉熵

$\frac{\partial y_{t,j}'}{\partial z_{t,i}}=-\frac{e^{z_{t,j}} e^{z_{t,i}}} {({\sum_k e^{z_{t,k}}})^2}=-\frac{e^{z_{t,j}}} {\sum_k e^{z_{t,k}}}\frac{e^{z_{t,i}}} {\sum_k e^{z_{t,k}}}=-y_{t,j}' y_{t,i}'$

偏导数的值，将两者的交叉熵相加，求的整个的熵

$ \frac{\partial L_t}{\partial z_t}=(-\sum_{t,i}\frac{ y_{t,i}}{y_{t,i}'}) \frac{\partial y_{t,i}'}{\partial z_{t,i}}  -\frac{ y_{t,i}}{y_{t,i}'}y_{t,i}'(1-y_{t,i}')+  \sum_{i,i \neq j}  \frac{ y_{t,i}} {y_{t,j}'}y_{t,i}' y_{t,j}'$

$= -y_{t,i}+y_{t,i}y_{t,i}'+  \sum_{i,i \neq j} y_{t,i} y_{t,i}'=-y_{t,i}+y_{t,i}'  \sum_i y_{t,i}= y_{t,i}'-y_{t,i} $

在t时刻对V的偏导

$\frac{\partial L_t}{\partial V}=\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial V } =(y_{t,i}'-y_{t,i} )S_t$

最终的损失，把各个时刻的相加则可得到。整个循环一遍，会改变参数，并不是每个时刻更新。

$ \frac{\partial L}{\partial V}=\sum_t \frac{\partial L_t}{\partial V}$

 

2.对U的导数

对U的导数和对V的导数相似，

$ \frac{\partial L}{\partial U}=\sum_t \frac{\partial L_t}{\partial U}$

$\frac{\partial L_t}{\partial U}=\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial S_t }   \frac{\partial {S_t}}{\partial U}  $

由V得到如下值：

$\frac{\partial L_t}{\partial z_t }=(y_{t,i}'-y_{t,i} )$

$\frac{\partial {z_t}}{\partial S_t }=V$

$\frac{\partial {S_t}}{\partial U} =tanh' X_t$

所以

$\frac{\partial L_t}{\partial U}=(y_{t,i}'-y_{t,i} )Vtanh' X_t$

3.对W的导数

 对W的导数会有依赖项，故而需要求解依赖项。

$ \frac{\partial L}{\partial W}=\sum_t \frac{\partial L_t}{\partial W}$

$\frac{\partial L_t}{\partial W}=\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial S_t }   \frac{\partial {S_t}}{\partial W}  $

由V得到如下值：

$\frac{\partial L_t}{\partial z_t }=(y_{t,i}'-y_{t,i} )$

$\frac{\partial {z_t}}{\partial S_t }=V$

$\frac{\partial {S_t}}{\partial W} =\frac{\partial {S_t}}{\partial W} +\frac{\partial {S_t}}{\partial S_{t-1}} \frac{\partial {S_{t-1}}}{\partial W}+\frac{\partial {S_t}}{\partial S_{t-1}} \frac{\partial {S_{t-1}}}{\partial S_{t-2}}  \frac{\partial {S_{t-2}}}{\partial W}\cdot\cdot\cdot $

总结起来：

$\frac{\partial {S_t}}{\partial W}=\sum_k^T\prod_{t=k+1}^{T} \frac{\partial {S_t}}{\partial S_{t-1}}\frac{\partial {S_k}}{\partial S_W}$

$\frac{\partial L_t}{\partial W}=\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial S_t }   \frac{\partial {S_t}}{\partial W} =\frac{\partial L_t}{\partial z_t }  \frac{\partial {z_t}}{\partial S_t } \sum_k^T\prod_{t=k+1}^{T} \frac{\partial {S_t}}{\partial S_{t-1}}\frac{\partial {S_k}}{\partial S_W}$

所以

$\frac{\partial L_t}{\partial U}=(y_{t,i}'-y_{t,i} )Vtanh'  \sum_k^T\prod_{t=k+1}^{T} \frac{\partial {S_t}}{\partial S_{t-1}}\frac{\partial {S_k}}{\partial S_W}$