Batch Normalization
一、Internal Covariate Shift
论文提出BN是用来解决“Internal Covariate Shift”问题的。如果输入数据经常变换,那么网络模型很难学到泛化的特征。对于深度学习这种包含很多隐层的网络结构,在训练过程中,因为各层参数不停在变化,所以每个隐层都会面临covariate shift的问题,也就是在训练过程中,隐层的输入分布老是变来变去,这就是所谓的“Internal Covariate Shift”,Internal指的是深层网络的隐层,是发生在网络内部的事情,而不是covariate shift问题只发生在输入层。
然后提出了BatchNorm的基本思想:让每个隐层节点的激活输入分布固定下来呢?这样就避免了“Internal Covariate Shift”问题了。
二、加速收敛
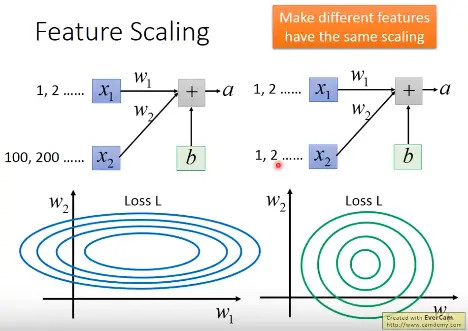
在没有进行BN之前,如果两个输入数据$x_1$,$x_2$的分布的量级差别很大的话,导致$x_2$对计算结果的影响比较大(图左),所以训练的时候,横纵方向上需要给与不同的training rate,在$x_1$方向需要一个更大的learning rate,使参数快速的变大,才能平衡$x_2$影响的结果,不过这样做的办法却不见得很简单,因为学习率不好控制。如果做了normalization之后,输入数据是同一个量级,使得error surface看起来比较接近正圆的话(图右),就可以使训练容易得多,从而加速收敛。
三、解决梯度消失和梯度爆炸
因为深层神经网络在做非线性变换前的激活输入值(就是那个$y=wx+b$,$x$是输入)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值$wx+b$是大的负值或正值),所以这导致反向传播时低层神经网络的梯度消失.BN之后,因为大权重有小梯度,这就不怕bp导致梯度放大,引起梯度爆炸。
四、BN其他优点
1.允许使用较大的学习率
分布较为一致,较大的学习率也不会导致不稳定的学习,较大的学习率可以避免进入局部最优,也能够加速收敛。
2.可以不需要小心翼翼地设置权重初始化
初始化对学习的影响减小了,可以不那么小心地设置初始权重。举例来说,对于一个单元的输入值,不管权重w,还是放缩后的权重kw,BN过后的值都是一样的,这个k被消掉了,对于学习来说,激活值是一样的。$\frac{kw-k\bar{w}}{k\sqrt{\sigma }}$,可以看到k被消掉。
3.减小对正则的需要
而导致overfitting往往是数据很大导致,而BN就使数据变小,overfitting现象就可以得到一定的缓解。所以可以减小或者不用dropout。
五、BN具体执行流程
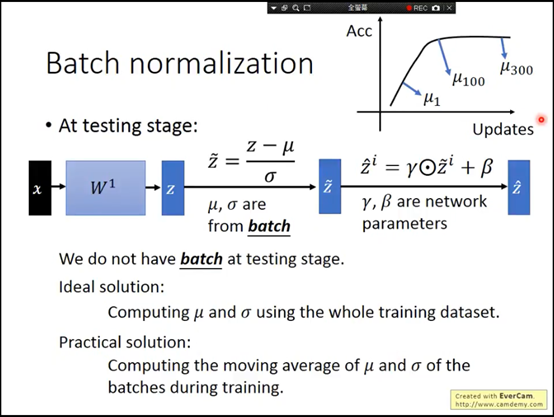
我们可能不希望所有的数据总是均值为0,方差为1。更好的模拟原始的数据。
$y_i\gets\hat{\gamma x_i}+\beta\equiv BN_{\gamma,\beta}x_i$
参考:
https://www.cnblogs.com/guoyaohua/p/8724433.html
https://www.jianshu.com/p/b4d186cca6be



