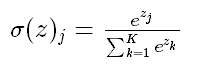激活函数

激活函数的作用

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。故而激活函数可以增加模型的表达能力。

1.sigmoid函数

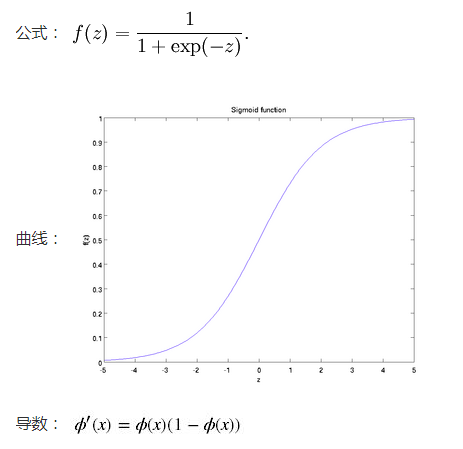
sigmoid函数也叫 Logistic 函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。

A.  优点

在特征相差比较复杂或是相差不是特别大时效果比较好。

B.  缺点

激活函数计算量大，反向传播求误差梯度时，求导涉及除法

反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练

Sigmoids函数收敛缓慢。 

下面解释为何会出现梯度消失：

sigmoid 原函数及导数图形如下

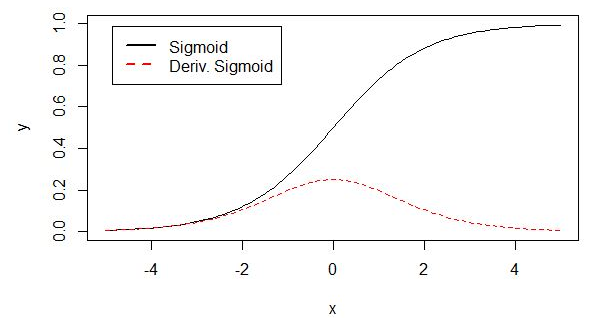
由图可知，导数从 0 开始很快就又趋近于 0 了，易造成“梯度消失”现象。

  2.   tanh函数

 

 

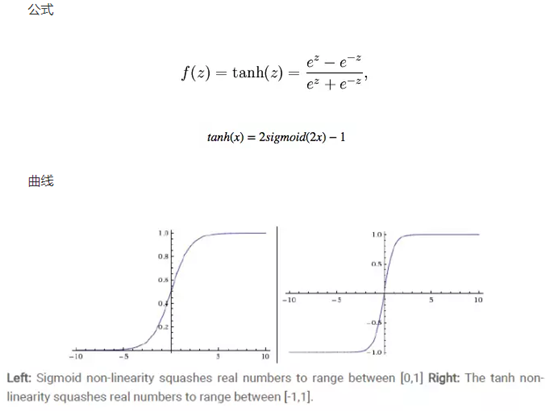
取值范围为[-1,1]。

tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。

A.  优点

与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。

B.  缺点

tanh一样具有软饱和性，从而造成梯度消失，在两边一样有趋近于０的情况 

3.   ReLU函数

 

 

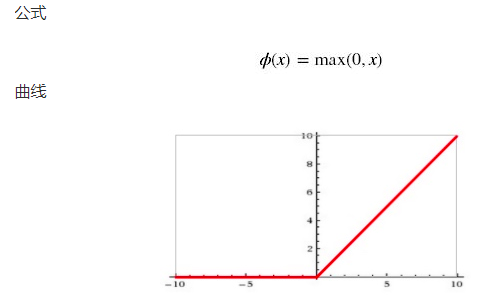
 取值范围[0,正无穷]

A.  优点

ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。

B.  缺点

随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。与sigmoid类似，ReLU的输出均值也大于0，偏移现象和 神经元死亡会共同影响网络的收敛性。   

针对在x<0的硬饱和问题，我们对ReLU做出相应的改进，使得 

 

 

 

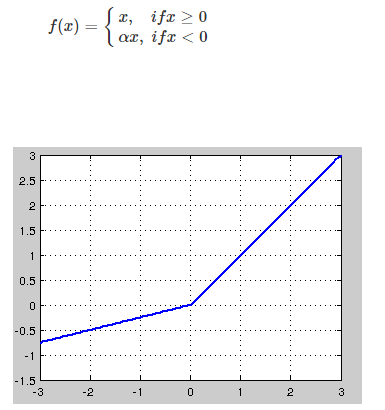
这就是Leaky-ReLU, 而P-ReLU认为，α也可以作为一个参数来学习，原文献建议初始化a为0.25，不采用正则。

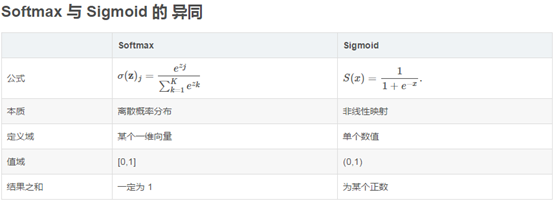
4.  softmax函数

Softmax - 用于多分类神经网络输出