L1和L2 详解(范数、损失函数、正则化)

一、易混概念

对于一些常见的距离先做一个简单的说明

1.欧式距离

假设X和Y都是一个n维的向量，即$X=（x_1, x_2, x_3, … x_n），Y=（y_1, y_2, y_3, … y_n）$

则欧氏距离：$D(X,Y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}$

2.L2范数

假设X是n维的特征$X=（x_1, x_2, x_3, … x_n）$ 

L2范数：$||X||_2=\sqrt{\sum_{i=1}^nx_i^2}$

3.闵可夫斯基距离

这里的p值是一个变量，当p=2的时候就得到了欧氏距离。

$D(X,Y)=(\sum_{i=1}^n|x_i-y_i|^p)^{\frac{1}{p}}$

4.曼哈顿距离

来源于美国纽约市曼哈顿区，因为曼哈顿是方方正正的。

$D(X,Y)=\sum_{i=1}^n|x_i-y_i|$

二、损失函数

L1和L2都可以做损失函数使用。

1.  L2损失函数

L2范数损失函数，也被称为最小平方误差（LSE）。它是把目标值$y_i$与估计值$f(x_i)$的差值的平方和最小化。一般回归问题会使用此损失，离群点对次损失影响较大。

$L=\sum_{i=1}^n(y_i−f(x_i))^2$

2.  L1损失函数

也被称为最小绝对值偏差（LAD），绝对值损失函数（LAE）。总的说来，它是把目标值$y_i$与估计值$f(x_i)$的绝对差值的总和最小化。

$L=\sum_{i=1}^n|y_i−f(x_i)|$ 

3.  二者对比

与最小平方相比，最小绝对值偏差方法的鲁棒性更好。因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数大的多，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

 

三、正则化

1.  正则化为什么可以避免过拟合？

正规化是防止过拟合的一种重要技巧。正则化通过降低模型的复杂性， 达到避免过拟合的问题。

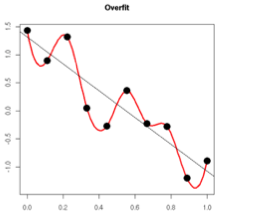
过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。

 

 

 

2.  L1正则

L1正则常被用来进行特征选择，主要原因在于L1正则化会使得较多的参数为0，从而产生稀疏解，我们可以将0对应的特征遗弃，进而用来选择特征。一定程度上L1正则也可以防止模型过拟合。

假设$L(W)$是未加正则项的损失，$\lambda$是一个超参，控制正则化项的大小。

则最终的损失函数：$L=L(W)+\lambda \sum_{i=1}^n |w_i|$

3.  L2正则

主要用来防止模型过拟合，直观上理解就是L2正则化是对于大数值的权重向量进行严厉惩罚。

则最终的损失函数：$L=L(W)+\lambda \sum_{i=1}^n w_i^2$

 

4.  为什么L1会产生稀疏解

稀疏性：很多参数值为0。

1）梯度的方式：

对其中的一个参数$w_i$计算梯度，其他参数同理，$\eta$是步进，$sign(w_i)$是符号函数。

L1的梯度：

$L=L(W)+\lambda \sum_{i=1}^n |w_i|$

$\frac{\partial L}{\partial w_i}=\frac{\partial L(W)}{\partial w_i}+\lambda sign(w_i)$

$w_i=w_i-\eta \frac{\partial L(W)}{\partial w_i}-\eta \lambda  sign(w_i)$

L2的梯度：

$L=L(W)+\lambda \sum_{i=1}^n w_i^2$

$\frac{\partial L}{\partial w_i}=\frac{\partial L(W)}{\partial w_i}+2\lambda w_i$

$w_i=w_i-\eta \frac{\partial L(W)}{\partial w_i}-\eta 2\lambda w_i$

当$w_i$小于1的时候，L2的惩罚项会越来越小，而L1还是会非常大，所以L1会使参数为0，而L2很难。

2）图形的方式：

损失函数L与参数$w$的关系图，绿点是最优点。

 

如果加上L2正则，损失函数L为$L+\lambda w^2$，对应的函数是蓝线，最优点是黄点。

 

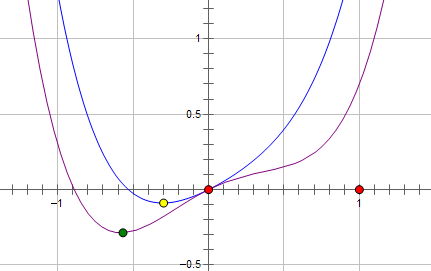
如果是加上L1损失，那么损失函数L是$L+\lambda |w|$，对应的函数是粉线，最优点是红点，参数$w$变为0。

 

 

两种正则化，能不能将最优的参数变为0，取决于最原始的损失函数在0点处的导数，如果原始损失函数在0点处的导数$\frac{\partial L}{\partial w}$不为0，则加上L2正则化项$2 \lambda w$之后，导数依然不为0,说明在0这点不是极值点，最优值不在w=0处。

而施加 $L1 =L+\lambda |w|$正则项时，导数在$w=0$这点不可导。不可导点是否是极值点，就是看不可导点左右的单调性。单调性可以通过这个点左、右两侧的导数符号判断，导数符号相同则不是极值点，左侧导数正，右侧导数负，则是极小值，左侧导数负，右侧导数正，极大值。

根据极值点判断原则，$w=0$左侧导数$\frac{\partial L1}{\partial w}=\frac{\partial L}{\partial w}-\lambda$，只要正则项的系数 $\lambda$ 大于$\frac{\partial L}{\partial w}$,那么左侧导数小于0，$w=0$右侧导数$\frac{\partial L1}{\partial w}=\frac{\partial L}{\partial w}+\lambda > 0$，所以$w=0$ 就会变成一个极小值点，所以L1经常会把参数变为0，产生稀疏解。