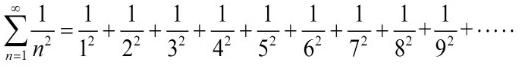级数初步
写在前面:
高考复习笔记

http://discordthege.deviantart.com/art/Free-pegasus-colonist-675224065
|
目录
|
定义
|
级数是指将数列的项依次用加号连接起来的函数 典型的级数有正项级数、交错级数、幂级数、傅里叶级数等 ——bia度百科
数列,是以正整数集(或它的有限子集)为定义域的函数,是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项,以此类推,排在第n位的数称为这个数列的第n项,通常用an表示 著名的数列有斐波那契数列,卡特兰数,杨辉三角等 ——bia度百科 |
历史
数列是一个古老的数学课题,我国对数列概念的认识很早,例如《周髀算经》里谈到:“在周城的平地立八尺高的周髀(即表竿),日中测影,在二十四节气中,冬至影长1丈3尺5寸,以后每一节气递减9寸55/6分;夏至影最短,仅长1尺6寸,以后每一节气又递增9寸55/6分”。这是等差数列的概念。《易传·系辞》:“河出图,洛出书,圣人则之;两仪生四象,四象生八卦”。这是世界数学史上有关等比数列的最早文字记载。我国古代还给出了一个无穷递缩等比数列,记载在《庄子·天下篇》中:“一尺之锤,日取其半,万世不竭。”而《九章算术》“衰分”一章,主要讲的就是分配比例及等差、等比数列等问题
在外国数学发展的早期也有许多人研究过数列这一课题。例如,在古巴比伦晚期的泥版文书中,有按级递减分物的等差数列问题,其中有一个问题大意是:10个兄弟分100两银子, 兄长最多,以此减少相同数目。现知第八兄弟分得6两,问相邻两兄弟相差多少?又如,在古埃及《阿美斯纸草书》上画有一图,在7、49、343、2401、16807数字边分别画着人、猫、鼠、大麦和量器。只有画作,却没有任何文字说明,因此成了一道流传的数谜。后人解出了这道数谜,认为图案要表达的意思是说:有7个人,每人畜养7只猫,每只猫捕食7只老鼠,而每只老鼠先前偷食了7株麦穗,每株麦穗能装满7个量杯......这可算是最早的等比数列了
——http://www.360doc.com/content/16/0720/10/26166517_576971392.shtml
常见类型
有穷数列、无穷数列
项数有限的数列为“有穷数列”;项数无限的数列为“无穷数列”
递增数列、递减数列、摆动数列
从第2项起,每一项都大于它的前一项的数列叫做递增数列
从第2项起,每一项都小于它的前一项的数列叫做递减数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列叫做摆动数列(摇摆数列)
周期数列
各项呈周期性变化的数列叫做周期数列
常数列
各项相等的数列叫做常数数列
等差数列、等比数列
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列(arithmetic sequence),这个常数叫做等差数列的公差(common difference),公差通常用字母d表示
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列(geometric sequence),这个常数叫做等比数列的公比(common ratio),公比通常用字母q表示
典型数列
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家Fibonacci以兔子繁殖为例子而引入,故又称为“兔子数列”
在数学上,斐波那契数列以如下被以递推的方法定义:
F(1)=1,F(2)=1,F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
矩阵乘法得第n项C++:
1 #include<bits/stdc++.h> 2 #define re register 3 4 typedef long long int ll; 5 using namespace std; 6 7 int const MOD=100007; 8 int n; 9 struct MART{ll mart[2][2];}base; 10 11 MART mul(MART a,MART b) 12 { 13 MART ans; 14 memset(ans.mart,0,sizeof(ans.mart)); 15 for(re int i=0;i<=1;++i) 16 for(re int j=0;j<=1;++j) 17 for(re int k=0;k<=1;++k) 18 { 19 ans.mart[i][j]+=a.mart[i][k]*b.mart[k][j]; 20 ans.mart[i][j]%=MOD; 21 } 22 23 return ans; 24 } 25 26 MART martxmul(int k) 27 { 28 MART ans; 29 ans.mart[0][0]=2;ans.mart[0][1]=1; 30 ans.mart[1][0]=1;ans.mart[1][1]=1; 31 while(k){ 32 if(k&1) ans=mul(ans,base); 33 k>>=1; 34 base=mul(base,base); 35 } 36 return ans; 37 } 38 39 int main(int arg,char *argv[],char *enc[]) 40 { 41 base.mart[0][0]=1;base.mart[0][1]=1; 42 base.mart[1][0]=1;base.mart[1][1]=0; 43 44 scanf("%d",&n); 45 46 printf("%d",martxmul(n-3).mart[0][0]); 47 48 return 0; 49 }
卡特兰数
卡特兰数又称卡塔兰数(Catalan number),是组合数学中一个常出现在各种计数问题中出现的数列,以比利时的数学家Catalan的名字来命名
卡特兰数Cn满足以下递推关系:
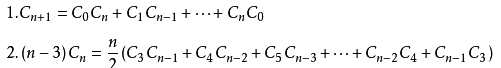
卡特兰数解决出入栈方案数问题C++:
1 #include<bits/stdc++.h> 2 #define re register 3 4 typedef long long int ll; 5 using namespace std; 6 7 const int MAXN=10010; 8 ll h[MAXN],n; 9 10 /* 11 h(n)=h(0)*h(n-1)+h(1)*h(n-2)+...+h(n-1)h(0) 12 (n>=2) 13 */ 14 int main(int arg,char *argv[],char *enc[]){ 15 scanf("%lld",&n); 16 h[0]=1;h[1]=1; 17 for(re ll i=2;i<=n;i++) 18 for(re ll j=0;j<=i-1;j++) 19 h[i]+=h[j]*h[i-j-1]; 20 for(re ll i=0;i<=n;i++) 21 printf("h[%lld] %lld\n",i,h[i]); 22 return 0; 23 } 24 /* 25 首先,我们设h(n)=序列个数为n的出栈序列种数 26 (栈直到整个过程结束时才空) 27 */
杨辉三角
杨辉三角,是二项式系数在三角形中的一种几何排列
在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现,书中载有“开方作法本源”图,注明“贾宪用此术”。而在欧洲,Pascal在1654年发现这一规律,所以这个表又叫做Pascal三角形
输出杨辉三角图形前n行C++:
1 #include<bits/stdc++.h> 2 #define re register 3 4 using namespace std; 5 6 const int maxn=15,m=2*maxn-1; 7 int n,tmp; 8 int arr[maxn+1][m]={0}; 9 10 int main(int arg,char *argv[],char *enc[]){ 11 scanf("%d",&n); 12 for(re int i=0;i<n;++i){ 13 arr[i][n-i-1]=1; 14 arr[i][n+i-1]=1; 15 16 } 17 for(re int i=2;i<n;++i) 18 for(re int j=n-i+1;j<n-2+i;j=j+2) 19 arr[i][j]=arr[i-1][j-1]+arr[i-1][j+1]; 20 for(re int i=0;i<n;++i){ 21 //for(re int j=0;j<n-i-1;++j) cout << " "; 22 tmp=1; 23 for(re int j=n-i-1;tmp<i+2;j=j+2){ 24 cout << setw(4) << arr[i][j] << " "; 25 ++tmp; 26 } 27 cout<<endl; 28 } 29 return 0; 30 }
其他
常用数列求和解题方法
公式求和法
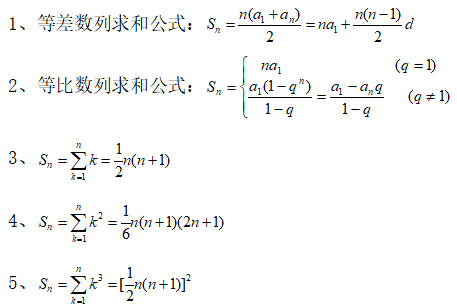
错位相减法
求数列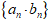 和
和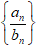 的前n项和,数列
的前n项和,数列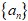 ,
,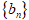 分别为等差与等比数列。求和时在求式的两边承以公比
分别为等差与等比数列。求和时在求式的两边承以公比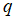 后,与原数列的和作差,即
后,与原数列的和作差,即 ,然后求
,然后求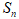 即可
即可
倒序相加法
将数列反序,再把正序与倒序对应项相加,使相加后的数列为一个简单数列,化繁为简,化未知为已知
分组求和法
其通项是几项等差数列、等比数列或易求和数列通项的和(差)式。若将这类数列适当拆开,可分为几个等差、等比、常见易求和的数列,然后通过重新组合的方法,使其转化为几个等差数列、等比数列,或转化为易求和数列的前n项求和,再将其合并,即可求出原数列的前n项和
裂项相消法
如果一个数列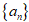 的通项能拆成两项之差,即
的通项能拆成两项之差,即 的每一项都可按此法化为某两项之差,然后重新组合,在求和时可以将一些正负项相互抵消,采用对消的方法求出到求和的目的
的每一项都可按此法化为某两项之差,然后重新组合,在求和时可以将一些正负项相互抵消,采用对消的方法求出到求和的目的
累加法
先引进一个恒等式,再通过把几个等式累加,可达到目的。一般引用的恒等式比数列通项高一次方,且是两个连续自然数的一定次方的差,列出含有通项的几个恒等式,通过迭加消去中间某些项,最后求得和式的一种方法
合并求和法
有些数列可以根据数列的特点,合理合并,从而简化运算。对一些特殊的数列,若将相邻两项或某些项合并在一起就具有某种特殊的性质,或呈现出一定的规律,则在数列求和时,可考虑把这些项放在一起先配对(并项)求和,得到一个新的容易求和的数列,然后再求和
——https://wenku.baidu.com/view/511c9b0ea8956bec0875e337.html
证明数列不等式的方法
先放缩再求和
1放缩后成等差数列
2放缩后成等比数列
3放缩后成差比数列
4放缩后为裂项相消
先求和再放缩
——https://wenku.baidu.com/view/30a6a93fcc7931b764ce1508.html