立体几何
写在前面:
高考复习笔记

http://discordthege.deviantart.com/art/Agrarian-Idyll-686018372
|
目录 |
角
角
定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形
取值范围:R
倾斜角
定义:平面直角坐标系内,当直线l与x轴相交时,取x轴作为基准, x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角
取值范围:[0°, 180°)
直线到角
定义:平面内,直线l1按逆时针方向旋转到与l2重合时所旋转的角,叫做l1到l2的角
取值范围:(0°, 180°)
直线夹角
定义:平面内,两直线相交,其中的锐角或直角叫做两直线的夹角
取值范围:(0°, 90°]
异面直线所成角
定义:有直线a与b是异面直线,经过空间一点O,作直线a',b',并使a'//a,b'//b,则把a'和b'所成的锐角或直角叫做异面直线a和b所成的角
取值范围:(0°, 90°]
平面向量所成角
定义:已知两个非零向量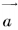 和
和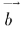 ,作
,作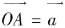 ,
,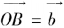 ,则
,则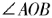 即为平面向量所成角
即为平面向量所成角
取值范围:[0°, 180°]
斜线与平面所成角
定义:平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角
取值范围:(0°, 90°)
二面角
定义:从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面
取值范围:[0°, 180°]
二面角的平面角
定义:以二面角的棱上任意一点为端点,在两个面内分别做垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角
取值范围:[0°, 180°]
辐角
定义:复数的辐角是指复数在复平面上对应的向量和正向实数轴所成的有向角。复数的辐角值可以是一切实数,但相差360°
取值范围:R
辐角主值
定义:复数的辐角在(-180°, 180°]之间的那个角
取值范围:(-180°, 180°]
直线、平面平行或垂直的判定
直线与平面平行的判定
①直线和平面在空间平面永无交点,则直线和平面平行(定义)
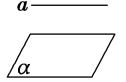
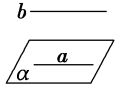
②平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行
平面与平面平行的判定
①如果两个平面无公共点,则称这两个平面平行(定义)
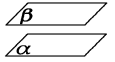
②一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行
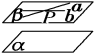
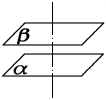
③如果两个平面同时垂直于一条直线,那么这两个平面垂直
直线和平面垂直的判定
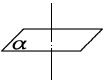
①如果直线l和平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α(定义)
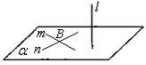
②一条直线与一个平面内的两条相交直线都垂直,则这条直线与该平面垂直
平面和平面垂直的判定
①两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直(定义)
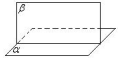
②一个平面过另一个平面的垂线,则这两个平面垂直
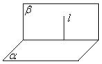
直线、平面平行或垂直的性质
直线与平面平行的性质
①一条直线与一个平面平行,则这条直线与该平面无交点
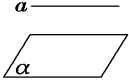
②一条直线和一个平面平行,则过这条直线的任一平面与此平面相交,这条直线和交线平行
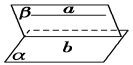
平面与平面平行的性质
①如果两个平行平面同时和第三平面相交,那么他们的交线平行
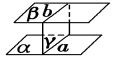
②如果两个平面平行,那么其中一个平面内的直线平行于另一个平面

直线和平面垂直的性质
①如果两个平行平面同时和第三平面相交,那么他们的交线平行
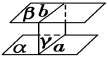
②如果两个平面平行,那么其中一个平面内的直线平行于另一个平面

平面和平面垂直的性质
①如果两个平面垂直,那么一个平面内垂直于它们交线的直线与一个面平垂直

空间向量求角
①证明要利用的三条直线两两垂直
②建立空间直角坐标系(右手直角坐标系,这姿势是让人做的??)
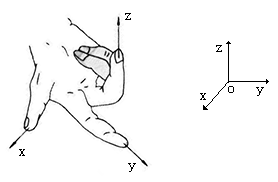
③求出空间中点的坐标,求出所需向量坐标
④使用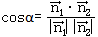 求解
求解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号