正态分布
写在前面:
高考复习笔记

|
目录
|
定义
|
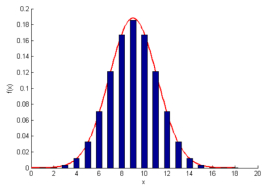
正态分布(/常态分布/高斯分布)是一个非常常见的连续概率分布,是连续随机变量概率分布的一种,自然界、人类社会、心理和教育中大量现象均按正态形式分布,例如能力的高低,学生成绩的好坏等都属于正态分布。它随随机变量的平均数、标准差的大小与单位不同而有不同的分布形态 正态分布在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线 正态分布曲线有以下性质: 集中性:正态曲线的高峰位于正中央,即均数所在的位置 对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交 均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降 曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100% ——bia度百科 |
历史
正态分布最早是De Moivre在1734年发表的一篇关于二项分布文章中提出的,当二项随机变量的位置参数n很大及形状参数p为1/2时,则所推导出二项分布的近似分布函数就是正态分布。Laplace在1812年发表的《分析概率论》中对De Moivre的结论作了扩展到二项分布的位置参数为n及形状参数为1>p>0时。
Laplace在误差分析试验中使用了正态分布。Legendre于1805年引入最小二乘法这一重要方法;而Gauss则宣称他早在1794年就使用了该方法,并通过假设误差服从正态分布给出了严格的证明。
“钟形曲线”这个名字可以追溯到Jouffret他在1872年首次提出这个术语"钟形曲面",用来指代二元正态分布。正态分布这个名字还被Charles S. Peirce、Francis Galton、Wilhelm Lexis在1875分别独立地使用。这个术语是不幸的,因为它反映和鼓励了一种谬误,即很多概率分布都是正态的。
这个分布被称为“Normal”或者“Gauss”正好是Stigler名字由来法则的一个例子,这个法则说“没有科学发现是以它最初的发现者命名的”。
——https://blog.csdn.net/hhaowang/java/article/details/83898881
分类
一维正态分布
X为随机变量,位置参数μ(期望值),尺度参数σ(标准差)
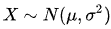
则其概率密度函数为
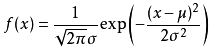
注:exp意为以e为底的指数函数
二维正态分布
X1、X2为随机变量,位置参数μ1、μ2(期望值),尺度参数σ1、σ2(标准差),结合紧密程度参数ρ
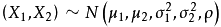
则其概率密度函数为
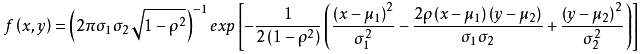
标准正态分布
标准正态分布是正态分布的一种,其期望值和标准差都是固定的,期望值为0,标准差为1
即μ=0,σ=1时:
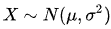
则其概率密度函数为
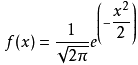
对数正态分布
对数正态分布是指一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布
如果数据是指数型发展的相乘(如细胞分裂后细胞个数)而不是相加,那么数据本身的对数服从正态分布,数据本身服从对数正态分布
对数正态分布从短期来看,与正态分布非常接近。但长期来看,对数正态分布向上分布的数值更多一些
性质
每个人都相信它(正态分布):实验工作者认为它是一个数学定理,数学研究者认为他是一个经验公式。
——Gabriel Lippmann
正态分布的前提
在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布
其中有三个要素:①独立②随机③相加
参数意义
μ是正态分布的位置参数,描述正态分布的集中趋势位置
σ描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中
ρ是描述二维正态分布两随机变量结合紧密程度的参数,从而确定变量的联合分布,不同的ρ对应不同的二维正态分布
曲线特点
正态曲线下:
横轴区间(μ-σ, μ+σ)内的面积为68.268949%。P{|X-μ|<σ} = 0.6827
横轴区间(μ-2σ, μ+2σ)内的面积为95.449974%。P{|X-μ|<2σ} = 0.9545
横轴区间(μ-3σ, μ+3σ)内的面积为99.730020%。P{|X-μ|<3σ} = 0.9973
由于“小概率事件”和假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件,认为在一次试验中该事件是几乎不可能发生的。由此可见X落在(μ-3σ, μ+3σ)以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间(μ-3σ, μ+3σ)看作是随机变量X实际可能的取值区间,这称之为正态分布的“3σ”原则
其他
为什么有很多数据不是正态分布?
在医学研究中很多分布就不是正态分布,对实施了前列腺癌症治疗的病人进行前列腺特异性抗原的检测,检测结果的分布不是正态分布:
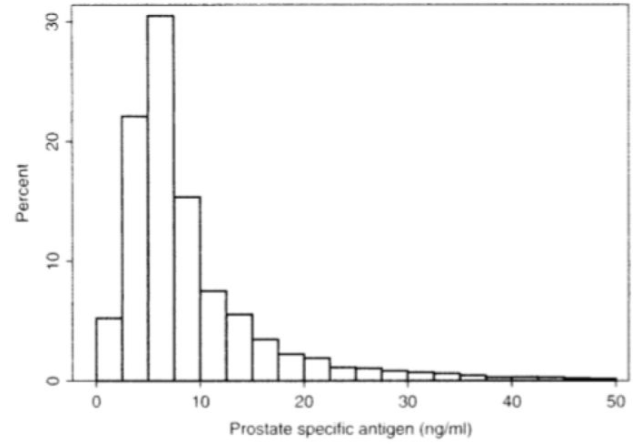
这里可能有两个原因导致了这一现象:
首先,样本取自实施了前列腺癌症治疗的病人,这些病人往往有各种各样的疾病,并不是全体人类样本,也就是说不够随机,所以结果很可能会偏向某一边。
其次,癌症并非是相加,癌细胞的分裂更像是乘法。数学中,可以通过对数来把乘法变为加法,对之前的数据取自然对数,结果就接近于正态分布了(这就是对数正态分布):
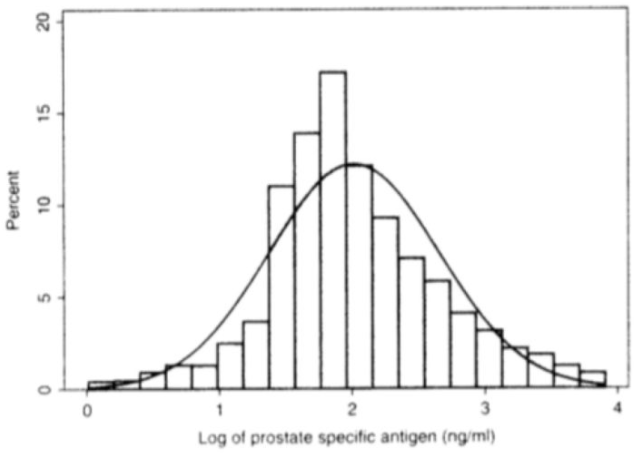
看上去还有点偏向左边,或许是因为采样不是取自全体人类,导致随机性不够。
以上数据及图片来自于《What is a p-value anyway? 34 Stories to Help You Actually Understand Statistics》。
——知乎 马同学

