试除法分解大整数
写在前面:
这篇博客是我在[◹]对 算术基本定理 的研究 中的一部分
- 试除法分解大整数
每次筛出一个素数p[i],看看其是否为要分解的正整数n的真因子
如果是的话,就除去n中所有的p[i]
是一种很朴素的尝试的思想,时间复杂度很大
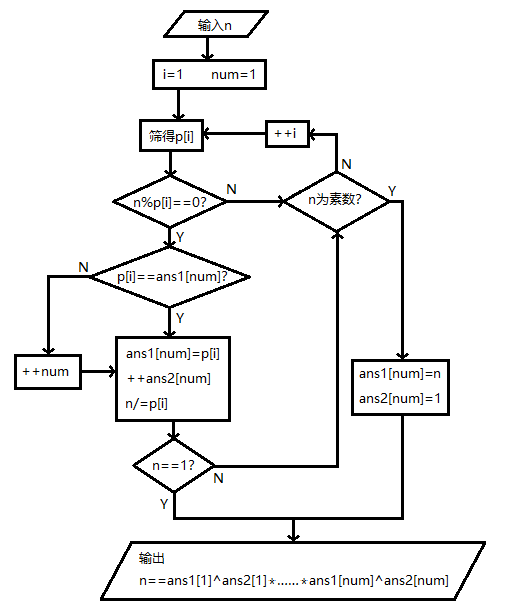
(注意,这张流程图是我的早期想法,和实际代码有点差别)
两个关键步骤的实现
筛出素数p[i]:[◹]三个线性筛法
判断素数:[◹]Miller-Rabin算法
代码实现的话,把主要步骤套进素数线性筛里面就好了
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int const MAXN=100010,MAXM=10010; 6 7 int n,preN,num=1; 8 int ans1[MAXM],ans2[MAXM]; 9 10 int prime[MAXN],tot; 11 bool notprime[MAXN]; 12 13 int ponyFE(int a,int b,int c) 14 { 15 int ans=1; 16 a%=c; 17 while(b!=0) 18 { 19 if(b&1) ans=(ans*a)%c; 20 b>>=1; 21 a=(a*a)%c; 22 } 23 return ans; 24 } 25 26 bool millerRabin(int x) 27 { 28 if(x==2) return 1; 29 if(!(x&1)||x==1) return 0; 30 31 bool pass; 32 int d=x-1,m; 33 while(!(d&1)) d>>=1;int tmp=d; 34 for(int i=1;i<=10;++i) 35 { 36 d=tmp;pass=0; 37 38 m=ponyFE(rand()%(x-2)+2,d,x); 39 if(m==1) continue; 40 else for(;d<x&&d>=0;m=(m*m)%x,d<<=1) 41 if(m==x-1){pass=1;break;} 42 43 if(!pass) return 0; 44 } 45 46 return 1; 47 } 48 49 int main(int argc,char *argv[],char *enc[]){ 50 51 scanf("%d",&n); 52 preN=n; 53 54 notprime[0]=1; 55 notprime[1]=1; 56 for(int i=2;i<=n;++i){ 57 if(!notprime[i]) 58 { 59 prime[tot++]=i; 60 61 if(n%i==0) 62 { 63 ans1[num]=i; 64 while(n%i==0){ 65 ++ans2[num]; 66 n/=i; 67 } 68 ++num; 69 } 70 71 if(n==1) break; 72 73 if(millerRabin(n)){ 74 ans1[num]=n; 75 ans2[num]=1; 76 ++num; 77 break; 78 } 79 } 80 for(int j=0; j<tot && i*prime[j]<=n;++j){ 81 notprime[i*prime[j]]=1; 82 if(i%prime[j]==0) break; 83 } 84 } 85 86 printf("%d==",preN); 87 for(int i=1;i<num-1;++i) 88 printf("%d^%d*",ans1[i],ans2[i]); 89 printf("%d^%d\n",ans1[num-1],ans2[num-1]); 90 91 return 0; 92 }
Java:
1 import java.util.Scanner; 2 3 class Pony{ 4 5 static int MAXN=100010,MAXM=10010; 6 7 static int n,preN,num=1; 8 static int[] ans1=new int[MAXM]; 9 static int[] ans2=new int[MAXM]; 10 11 static int tot; 12 static int[] prime=new int[MAXN]; 13 static boolean[] notprime=new boolean[MAXN]; 14 15 static int ponyFE(int a,int b,int c) 16 { 17 int ans=1; 18 a%=c; 19 while(b!=0) 20 { 21 if((b&1)==1) ans=(ans*a)%c; 22 b>>=1; 23 a=(a*a)%c; 24 } 25 return ans; 26 } 27 28 static boolean millerRabin(int x) 29 { 30 if(x==2) return true; 31 if((x&1)==0||x==1) return false; 32 33 boolean pass; 34 int d=x-1,m; 35 while((d&1)==0) d>>=1;int tmp=d; 36 for(int i=1;i<=10;++i) 37 { 38 d=tmp;pass=false; 39 40 m=ponyFE((int)(Math.random())%(x-2)+2,d,x); 41 if(m==1) continue; 42 else for(;d<x&&d>=0;m=(m*m)%x,d<<=1) 43 if(m==x-1){pass=true;break;} 44 45 if(!pass) return false; 46 } 47 48 return true; 49 } 50 51 public static void main(String[] args) throws Exception 52 { 53 Scanner cin=new Scanner(System.in); 54 55 n=cin.nextInt(); 56 preN=n; 57 58 notprime[0]=true; 59 notprime[1]=true; 60 for(int i=2;i<=n;++i){ 61 if(!notprime[i]) 62 { 63 prime[tot++]=i; 64 65 if(n%i==0) 66 { 67 ans1[num]=i; 68 while(n%i==0){ 69 ++ans2[num]; 70 n/=i; 71 } 72 ++num; 73 } 74 75 if(n==1) break; 76 77 if(millerRabin(n)){ 78 ans1[num]=n; 79 ans2[num]=1; 80 ++num; 81 break; 82 } 83 } 84 for(int j=0; j<tot && i*prime[j]<=n;++j){ 85 notprime[i*prime[j]]=true; 86 if(i%prime[j]==0) break; 87 } 88 } 89 90 System.out.printf("%d==",preN); 91 for(int i=1;i<num-1;++i) 92 System.out.printf("%d^%d*",ans1[i],ans2[i]); 93 System.out.printf("%d^%d\n",ans1[num-1],ans2[num-1]); 94 } 95 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号