更项减损术

写在前面：

　　这篇博客是我在[◹]对 算术基本定理 的研究 中的一部分

 

• 更相减损术

　　除了列举外，如何求解两个整数的最大公因数？

我们一直感觉，两个数的因数与两个数的差之间冥冥之中有着某种联系

　　别的先不说，来看一张打出来的表

　　一张看不出来什么，再看一张

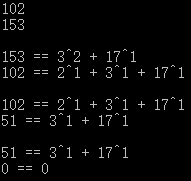
　　多看几张

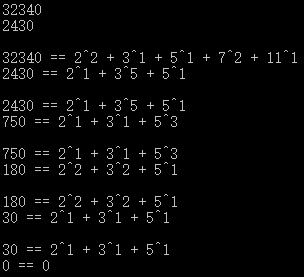
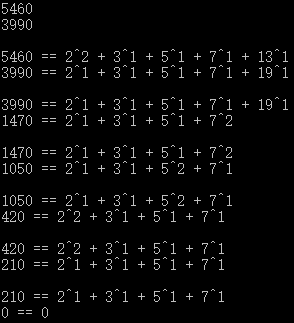
　　这几张表能说明什么呢？

　　我的想法是：

　　　　加减运算能够破坏一个数的标准分解结构(毕竟单项式拆成了多项式)

　　　　而除了两个(正整)数的公因子之外的因子，都可以看做多余的，加减运算能够破坏的只是这些多余的因子

　　　　反复进行加减，直到剩下的因数不能再被破坏(代码中体现为!b?)

　　　　剩下的那些因子之积就是GCD了

　　　　(初步的想法)

 

　　再想想，这不就是 乘法结合律 吗？？

 　　

　　来把两个数拆一下：

　　　　有两个数 a,b∈N*，a>b

　　　　根据算术基本定理，有

　　　　a == P₁^a1P₂^a2P₃^a3......P_n^an

　　　　b == P₁^b1P₂^b2P₃^b3......P_n^bn

　　　　再结合乘法结合律带入a，b，丢番图方程为：

　　　　蓝色部分即为a，b的最大公因数(所有质因子的积)

　　　　而因为a，b都是正整数，且规定a>b

　　　　在欧几里得算法中循环总是大数减小数(且两个数一定是正整数)

　　　　且规定直到再减就两个数相等，没有谁大谁小为止

　　　　则绿色部分最终的计算结果只能是1

此处将MOD运算看作对于每一轮减法的加速

　　　　那么答案就是a，b的最大公因数了！

若换成 MOD，那么就是每个质因数的指数之间来回减啊减啊，一直减到绿色部分质因数的指数都为0

　　精炼一下，就是：

　　　　任何一个数n∈N*，都可以拆成d'*n的形式(此时只有一个数，没有产生对比，则认为d'没有什么意义)

　　　　有两个数 a,b∈N*，a == d'*n₁，a == d'*n₂ (d'为a，b的最大公因数，a>b)

　　　　根据乘法结合律，有

a-b == d' * (n₁-n₂)

　　这样一来，乘法结合律就是算术基本定理从单项式到多项式的桥梁

　　(博主是瞎想的，如果有这方面的知识欢迎告知啦)

ps:博主高二，好多东西不知道啦