[Algorithm] Dynamic programming - 02 - Longest Common Subsequence - Drawing 2d matrix + back tracing

Write a function that takes in two strings and returns their longest common subsequence.

A subsequence of a string is a set of characters that aren't necessarily adjacent in the string but that are in the same order as they appear in the string. For instance, the characters ["a", "c", "d"] form a subsequence of the string "abcd", and so do the characters ["b", "d"]. Note that a single character in a string and the string itself are both valid subsequences of the string.

You can assume that there will only be one longest common subsequence.

Sample Input

str1 = "ZXVVYZW"
str2 = "XKYKZPW"

Sample Output

["X", "Y", "Z", "W"]

 

---

 

    ""	X	K	Y	K	Z	P	W
""	0	0	0	0	0	0	0   0
Z	0	0	0	0	0	1	1	1
X	0	1	1	1	1	1	1	1
V	0	1	1	1	1	1	1	1
V	0	1	1	2	2	2	2	2
Y	0	1	1	2	2	2	2	2
Z	0	1	1	2	2	3	3	3
W	0	1	1	2	2	3	3	4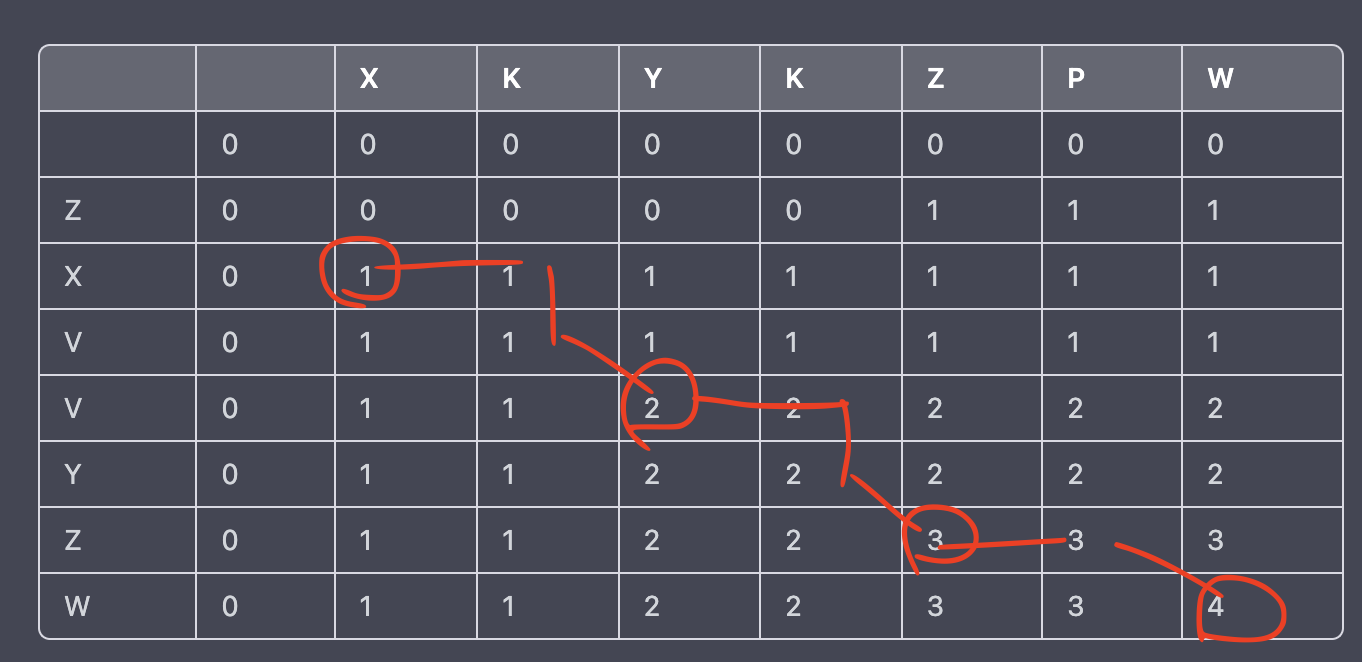

 

1. Start at cell (7, 7), which contains the length of the longest common subsequence of the entire strings.
2. If current value (4), is greater than (i-1, j) = 3, (i, j-1) = 3, then add str1[7] = W to the result array, then jump diagonally to (6,6)
3. Otherwise, if the value in cell (i-1, j) is greater than the value in cell (i, j-1), move up to cell (i-1, j).
4. Otherwise, move left to cell (i, j-1).
5. Repeat steps 2-4 until we reach cell (0, 0).

function longestCommonSubsequence(str1, str2) {
  const m = str1.length + 1;
  const n = str2.length + 1;

  const dp = Array.from({length: m}, () => Array.from({length: n}, () => 0))

  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      if (str1[i-1] !== str2[j-1]) {
        dp[i][j] = Math.max(
          dp[i-1][j],
          dp[i][j-1],
        )
      } else {
        dp[i][j] = 1 + dp[i-1][j-1]
      }
    }
  }
  console.log(dp)
  return backTracking(dp, str1)
}

function backTracking(dp, str1) {
  const res = []

  let i = dp.length - 1
  let j = dp[0].length - 1;

  while ( i !== 0 && j !== 0) {
    if (dp[i][j] === dp[i-1][j]) {
      i--;
    } else if (dp[i][j] === dp[i][j-1]) {
      j--;
    } else {
      res.unshift(str1[i-1])
      j--;
      i--;
    }
  }

  return res;
}

// Do not edit the line below.
exports.longestCommonSubsequence = longestCommonSubsequence;