树上启发式合并_训练总结+题目清单
前言：树上启发式合并(DSU on Tree)，是一个在O(nlogn) 时间内解决许多树上问题的有力算法，其对于树上离线问题的处理速度大于等于其他的算法，且更容易理解(个人认为处理与子树的关系牵涉很多)。具体思路大概就是先像树链剖分那样找到每个结点的重儿子，然后把所有轻儿子的贡献合并于重儿子(比较抽象吧~),当前结点操作完毕之后，再看如果当前结点是其父亲结点的一个轻儿子，那么该轻儿子贡献全部置0。对于重儿子的贡献保留。至于时间复杂度为什么是O(logn)，我也不太会证明，但是肯定比在线暴力对每个儿子操作其全部结点快，因为首先Dsu On Tree是个离线算法，你每次对当前结点的操作，实际是只要处理轻儿子结点(重儿子结点贡献已经有了)，这么来看你就较常规方法少了再遍历重儿子的那一步，时间复杂度自然而然就降了。
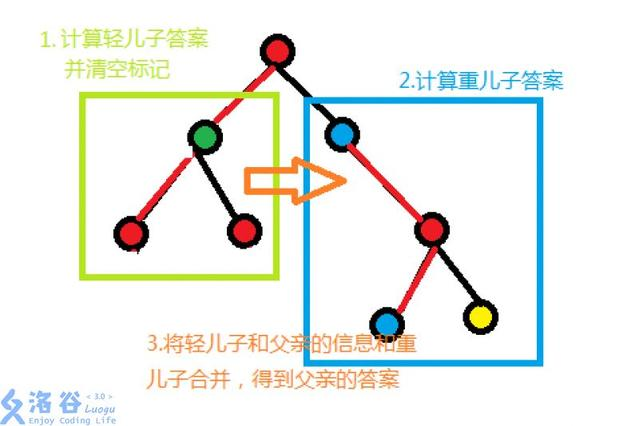←大概就是这个样子吧OvO
我觉得理解一个算法的，重要的一步是训练刷题+总结，所以我附上一些刷题题单，前面几个题会简单一些(CF2300分左右)，最后一个题有点难(CF2900分)
还有一道题是Wannafly Camp Day2E 阔立梯的树，我之前写过题解，是一个很不错的题:https://www.cnblogs.com/Anonytt/p/13080989.html
接下来我一道题一道题地写一下解析叭：
A：Codeforces-600E(Lomsat Gelral)
题意：对于每个子树，输出子树中出现次数最多的节点编号之和。（次数最多的编号有多个节点都要统计进去）
解法：这是一道比较模板的树上启发式合并题，每一次count，统计当前颜色col[u]出现的次数即cnt[col[u]]。如果其次数大于所有颜色中出现次数最多颜色的大小maxc,即把maxc更新成当前结点的颜色大小cnt[col[u]],同时更新sum。另外该题要求如果子树中出现颜色次数一样，那么和就等于这些相同颜色值大小和，所以你还需要特判更新一波。
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=1e5+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int col[maxn],cnt[maxn]; int siz[maxn],son[maxn]; void dfs(int u,int f){ siz[u]=1; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]){ son[u]=v; } } } ll ans[maxn],sum; int flag,maxc; void count(int u,int f,int val){ cnt[col[u]]+=val; if(cnt[col[u]]>maxc){ maxc=cnt[col[u]]; sum=col[u]; } else if(cnt[col[u]]==maxc) sum+=col[u]; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,bool keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,false); } if(son[u]){ dfs(son[u],u,true); flag=son[u]; } count(u,f,1); flag=0; ans[u]=sum; if(!keep){ count(u,f,-1); sum=maxc=0; } } int main(){ int n;scanf("%d",&n); mem(head,-1); rep(i,1,n) scanf("%d",&col[i]); rep(i,1,n-1){ int u,v;scanf("%d%d",&u,&v); add(u,v);add(v,u); } dfs(1,0); dfs(1,0,0); rep(i,1,n) printf("%lld ",ans[i]); puts(""); }
B：Codeforces-246E(Blood Cousins Return)
题意：给定一棵树，已知每个节点的父亲节点，和每个节点上的名字(字符串)，对于每个询问vi,ki，求子树vi内v的kth层儿子(子树内比子树根深度大k层的部分)中不重复名字的个数。
解法：因为有可能是森林，所以你需要统计一共有多少个树rootcnt,并记录每个数的根节点root[i](判断其是否为某个数根节点只需要看它父亲是不是0就行啦)，利用map离散化一下，就把名字当成颜色好了。同时count的时候也要注意某子树如果当前结点为u当前层中该颜色即col[u]是否在其他子树出现过，即也用map来记录一下，如果没有那ok，如果有的话，当前层次的颜色你就不需要再更新啦！另外值得一提的是：对于结点询问，如果只给你某个结点的v和第几层d，那么可以用vector<pair<int,int>> q[maxn]来记录，第一个q[u]记录结点v，q[u][i].first记录询问的id，q[u][i].second记录层次。然后你统计当前询问的时候，只需要看当前结点u是否充当v的时候q[u].size()是否>0，若如此则说明有询问坐落于该结点上。
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=1e5+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int n;map<string,int> mp;int c[maxn],root[maxn]; vector<pair<int,int> >q[maxn]; int siz[maxn],son[maxn],dep[maxn]; void dfs1(int u,int f){ dep[u]=dep[f]+1; siz[u]=1; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } int flag,ans[maxn]; int cnt[maxn]; map<pair<int,int>,int> pk; void count(int u,int f,int val){ if(val==1&&!pk[{dep[u],c[u]}]) cnt[dep[u]]+=val,pk[{dep[u],c[u]}]+=val; if(val==-1&&pk[{dep[u],c[u]}]) cnt[dep[u]]+=val,pk[{dep[u],c[u]}]+=val; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,0); } if(son[u]){ dfs(son[u],u,1); flag=son[u]; } count(u,f,1); for(int i=0;i<q[u].size();i++){ int id=q[u][i].first; int d=q[u][i].second; ans[id]=cnt[dep[u]+d]; } flag=0; if(!keep){ count(u,f,-1); } } int main(){ cin>>n;mem(head,-1); int cntcolor=0;int cntroot=0; rep(i,1,n){ string s;int x;cin>>s>>x; if(!mp[s]) mp[s]=++cntcolor; c[i]=mp[s]; if(!x){ ++cntroot; root[cntroot]=i; }else{ add(x,i);add(i,x); } } int m;cin>>m; rep(i,1,m){ int u,d;cin>>u>>d; q[u].push_back({i,d}); } rep(i,1,cntroot){ dfs1(root[i],0); } rep(i,1,cntroot){ dfs(root[i],0,0); } rep(i,1,m){ cout<<ans[i]<<endl; } }
C: Codeforces-1009F(Dominant Indices)
题意：给定一棵以 1 为根，n 个节点的树。设 d(u,x)为 u 子树中到 u 距离为 x 的节点数。对于每个点，求一个最小的 k，使得 d(u,k) 最大。
解法：这个其实也挺简单的，同样是记录每一层该颜色出现的次数，若该颜色次数大于等于(Hint!!)最大值就进行更新maxx和loc，你需要注意如果cnt[col[u]]和maxx一致，要把loc更新成最近的dep[u]，我就是这里没注意wa了一发，其实样例就能检测出来，如果是树链的情况的话。
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define pb push_back #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=1e6+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int n; int dep[maxn],siz[maxn],son[maxn]; void dfs1(int u,int f){ siz[u]=1; dep[u]=dep[f]+1; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } int flag,cnt[maxn],maxx,loc,ans[maxn]; void count(int u,int f,int val){ cnt[dep[u]]+=val; /* if(val>0&&cnt[dep[u]]>maxx){ maxx=cnt[dep[u]]; loc=dep[u]; } */ if(val>0&&cnt[dep[u]]>=maxx){ if(cnt[dep[u]]>maxx) maxx=cnt[dep[u]],loc=dep[u]; else if(cnt[dep[u]]==maxx&&dep[u]<loc){ loc=dep[u]; } } for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,0); } if(son[u]){ dfs(son[u],u,1); flag=son[u]; } count(u,f,1); ans[u]=loc-dep[u]; flag=0; if(!keep){ count(u,f,-1); maxx=0;loc=INF; } } int main(){ cin>>n;mem(head,-1);maxx=0;loc=INF; rep(i,1,n-1){ int u,v;cin>>u>>v; add(u,v);add(v,u); } dfs1(1,0); dfs(1,0,0); rep(i,1,n){ cout<<ans[i]<<endl; } }
D:Codeforces-375D(Tree and Queries)
题意:现有一棵 n 个点的树，点的编号从 1 起，树以 1 为根，每个点 i 都一个颜色 ci，接下来有 m 个询问，每次询问以 vj为根的子树中，求有多少种颜色，这些颜色在子树中出现的次数至少为 kj。
解法：直接统计就行，注意如果val是正的就{cnt[c[u]]+=val;vis[cnt[c[u]]]+=val;}，否则{vis[cnt[c[u]]]+=val;cnt[c[u]]+=val;}
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define pb push_back #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=1e5+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int n,m,c[maxn]; vector<pair<int,int> >q[maxn]; int siz[maxn],son[maxn],dep[maxn]; void dfs1(int u,int f){ dep[u]=dep[f]+1; siz[u]=1; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } int flag,cnt[maxn],vis[maxn],ans[maxn]; void count(int u,int f,int val){ if(val==1) {cnt[c[u]]+=val;vis[cnt[c[u]]]+=val;} else {vis[cnt[c[u]]]+=val;cnt[c[u]]+=val;} for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,0); } if(son[u]){ dfs(son[u],u,1); flag=son[u]; } count(u,f,1); for(int i=0;i<q[u].size();i++){ int id=q[u][i].first; int lim=q[u][i].second; ans[id]=vis[lim]; } flag=0; if(!keep){ count(u,f,-1); } } int main(){ scanf("%d%d",&n,&m);mem(head,-1); rep(i,1,n) scanf("%d",&c[i]); rep(i,1,n-1){ int u,v;scanf("%d%d",&u,&v); add(u,v);add(v,u); } rep(i,1,m){ int x,k;scanf("%d%d",&x,&k); q[x].pb({i,k}); } dfs1(1,0); dfs(1,0,0); rep(i,1,m){ cout<<ans[i]<<endl; } }
E:Codeforces-570D(Tree Requests)
题意：一棵以1为根的树，每个节点上都有1个字母，有m个询问。每次询问v对应的子树中，深度为h的这层节点的字母，能否打乱重排组成回文串。根的深度为1，每个点的深度为到根的距离。
解法：因为有26个字母，其实看做只有26个颜色，你每次count的时候统计cnt[dep[u]][c[u]]，c[u]数组大小开到26就行了，dep[u]数组开到5e5，所以不会炸数组，看是否是回文，你只需要统计该层中所有颜色%2后的值num，并统计num的和sum，若sum=0则说明是一个全是偶数的回文串，若sum=1说明这些结点中有一个颜色是单数的，当然这也是回文串的范畴(放在最中间),但是若sum>1了就不行，因为这样就不可构成回文串了。
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=5e5+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int n,m,c[maxn],ans[maxn]; vector<pair<int,int> >q[maxn]; int siz[maxn],son[maxn],dep[maxn]; void dfs1(int u,int f){ siz[u]=1;dep[u]=dep[f]+1; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } int flag,cnt[maxn][30]; void count(int u,int f,int val){ cnt[dep[u]][c[u]]+=val; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,0); } if(son[u]){ dfs(son[u],u,1); flag=son[u]; } count(u,f,1); for(int i=0;i<q[u].size();i++){ int id=q[u][i].first; int d=q[u][i].second; int num=0; rep(j,1,26){ if(cnt[d][j]&1) num++; } ans[id]=num>1?0:1; } flag=0; if(!keep){ count(u,f,-1); } } int main(){ scanf("%d%d",&n,&m);mem(head,-1); for(int i=2;i<=n;i++){ int u;scanf("%d",&u); add(u,i);add(i,u); } string s;cin>>s;s=" "+s; rep(i,1,n) c[i]=s[i]-'a'+1; dfs1(1,0); rep(i,1,m){ int x,y;scanf("%d%d",&x,&y); q[x].push_back(make_pair(i,y)); } dfs(1,0,0); rep(i,1,m){ if(ans[i]) puts("Yes"); else puts("No"); } }
F:Codeforces-208E(Blood Counsins)
题意：在一个森林中，如果两个节点a和b向上的第p个祖先相同，就称他们为p代表亲。(跟日常生活中有所不同，p不一定是他们的最近公共祖先)。 给出一些询问，问v的p代表亲的数量。
解法：这里就是反向思维来思考了，即求每个节点u的子树中，距离u节点距离为p的结点数量(记得最后减1即删去本身哦~)，这里就用到了倍增思想来揪出距离结点a长度为p的祖先是谁。
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=1e5+5; int tot,head[maxn]; struct E{ int to,next; }edge[maxn<<1]; void add(int u,int v){ edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } int n,fa[maxn][40],root[maxn]; void bz(){ for(int j=1;j<=30;j++){ for(int i=1;i<=n;i++){ fa[i][j]=fa[fa[i][j-1]][j-1]; } } } int siz[maxn],son[maxn],dep[maxn]; void dfs1(int u,int f){ fa[u][0]=f; dep[u]=dep[f]+1; siz[u]=1; //rep(i,1,20) fa[u][i]=fa[fa[u][i-1]][i-1]; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } vector<pair<int,int> >q[maxn]; int flag,cnt[maxn],ans[maxn]; void count(int u,int f,int val){ cnt[dep[u]]+=val; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==flag) continue; count(v,u,val); } } void dfs(int u,int f,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f||v==son[u]) continue; dfs(v,u,0); } if(son[u]){ dfs(son[u],u,1); flag=son[u]; } count(u,f,1); for(int i=0;i<q[u].size();i++){ int id=q[u][i].first; int d=q[u][i].second; ans[id]=cnt[d]-1; } flag=0; if(!keep){ count(u,f,-1); } } int main(){ cin>>n;mem(head,-1); int rootcnt=0; rep(i,1,n){ int x;cin>>x; if(!x) root[++rootcnt]=i; else{ add(x,i);add(i,x); } } rep(i,1,rootcnt) dfs1(root[i],0); bz(); int m;cin>>m; rep(i,1,m){ int u,p;cin>>u>>p; int d=dep[u]; for(int j=20;j>=0;j--){ if(p&(1<<j)) u=fa[u][j]; } q[u].push_back({i,d}); } rep(i,1,rootcnt) dfs(root[i],0,0); rep(i,1,m){ cout<<ans[i]<<" "; } cout<<endl; }
G:Codeforces-741D(Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths)
题意(这是算法发明者专门为这个算法量身订造的题目哦):一棵根为1 的树，每条边上有一个字符（a-v共22种）。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中最长的Dokhtar-kosh路径的长度。给你n个点构成的一棵树，树里面的每一条边有一个权值，求出每个子树里面能通过重排构成回文串的最大路径长度.
解法：首先我们需要从一个点来入手，容易发现字符只有22种，比较少，而满足重排后能构成回文串的条件是：每个字符出现次数都为偶数或出现次数为奇数的字符仅有一个。因此我们可以考虑将其压缩成0表示出现次数为偶数，1表示出现次数为奇数。而对于一个路径上的字符，我们只需考虑每个字符的出现次数，这样我们巧妙地把问题状压了一下,用一个整数就可以表达出所有符合条件的状态：0 或者 （1<<i）,0<=i<=21,总共22种。之后我们可以考虑维护一个值 dis[i] 表示 从 i 到 1 的路径上字符的状态，其实利用异或的性质，dis[i]就是从 1 到 i 路径里面所有字符表示的状态异或的答案。同时我们如果知道两个点，怎样求出两个点形成的状态呢，也是利用异或的性质，假设有两个点u和v，dis[u]^dis[v]^dis[lca(u,v)]^dis[lca(u,v)]其实就是答案，简化一下就是 dis[u]^dis[v]，因为两个点的lca上的部分会因为异或的性质抵消掉。那么我们就很容易发现如果两个节点之间形成的路径符合条件的话，那么dis[u]^dis[v] = 0 | (1<<i),1<=i<=21这里我们还需要在求每个子树的答案维护一个值，即f[dis[i]] 表示在以当前节点为根的子树中状态为dis[i] 的最大深度。然后我们先按照dsu on tree 套路，先去遍历每一个轻儿子，计算数据但是不保留，之后处理重儿子，计算数据并且保留，最后再计算轻儿子和当前节点对答案的贡献。具体过程参考代码，时间复杂度O(23nlogn)
#include<bits/stdc++.h> #define ll long long #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define endl '\n' #define eps 0.000000001 #define pb push_back #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0); using namespace std; const int INF=0x3f3f3f3f; const ll inf=0x3f3f3f3f3f3f3f3f; const int mod=1e9+7; const int maxn=5e5+5; int tot,head[maxn]; struct E{ int to,next,w; }edge[maxn<<1]; void add(int u,int v,int w){ edge[tot].to=v; edge[tot].w=w; edge[tot].next=head[u]; head[u]=tot++; } int dep[maxn],siz[maxn],son[maxn],dis[maxn],L[maxn],R[maxn],id[maxn],dfn; void dfs1(int u,int f){ dep[u]=dep[f]+1; siz[u]=1; L[u]=++dfn; id[dfn]=u; for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==f) continue; dis[v]=dis[u]^edge[i].w; dfs1(v,u); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } R[u]=dfn; } int ans[maxn],flag,f[maxn*10]; void calc(int u,int fa){ if(f[dis[u]]) ans[u]=max(ans[u],f[dis[u]]-dep[u]); rep(i,0,21){ if(f[dis[u]^(1<<i)]){ ans[u]=max(ans[u],f[dis[u]^(1<<i)]-dep[u]); } } f[dis[u]]=max(f[dis[u]],dep[u]); for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==fa||v==flag) continue; rep(j,L[v],R[v]){ int x=id[j]; if(f[dis[x]]) ans[u]=max(ans[u],f[dis[x]]+dep[x]-2*dep[u]); rep(k,0,21){ if(f[dis[x]^(1<<k)]){ ans[u]=max(ans[u],f[dis[x]^(1<<k)]+dep[x]-2*dep[u]); } } } rep(j,L[v],R[v]) f[dis[id[j]]]=max(f[dis[id[j]]],dep[id[j]]); } } void dfs(int u,int fa,int keep){ for(int i=head[u];i!=-1;i=edge[i].next){ int v=edge[i].to; if(v==son[u]||v==fa) continue; dfs(v,u,0); ans[u]=max(ans[u],ans[v]); } if(son[u]){ dfs(son[u],u,1); ans[u]=max(ans[u],ans[son[u]]); flag=son[u]; } calc(u,fa); flag=0; if(!keep){ rep(i,L[u],R[u]) f[dis[id[i]]]=0; } } int main(){ int n;cin>>n;mem(head,-1); rep(i,2,n){ int x;char s; cin>>x>>s; add(i,x,1LL<<(s-'a')); add(x,i,1LL<<(s-'a')); } dfs1(1,0); dfs(1,0,0); rep(i,1,n) cout<<ans[i]<<" "; }
