参考博客:https://www.cnblogs.com/onepixel/articles/7674659.html
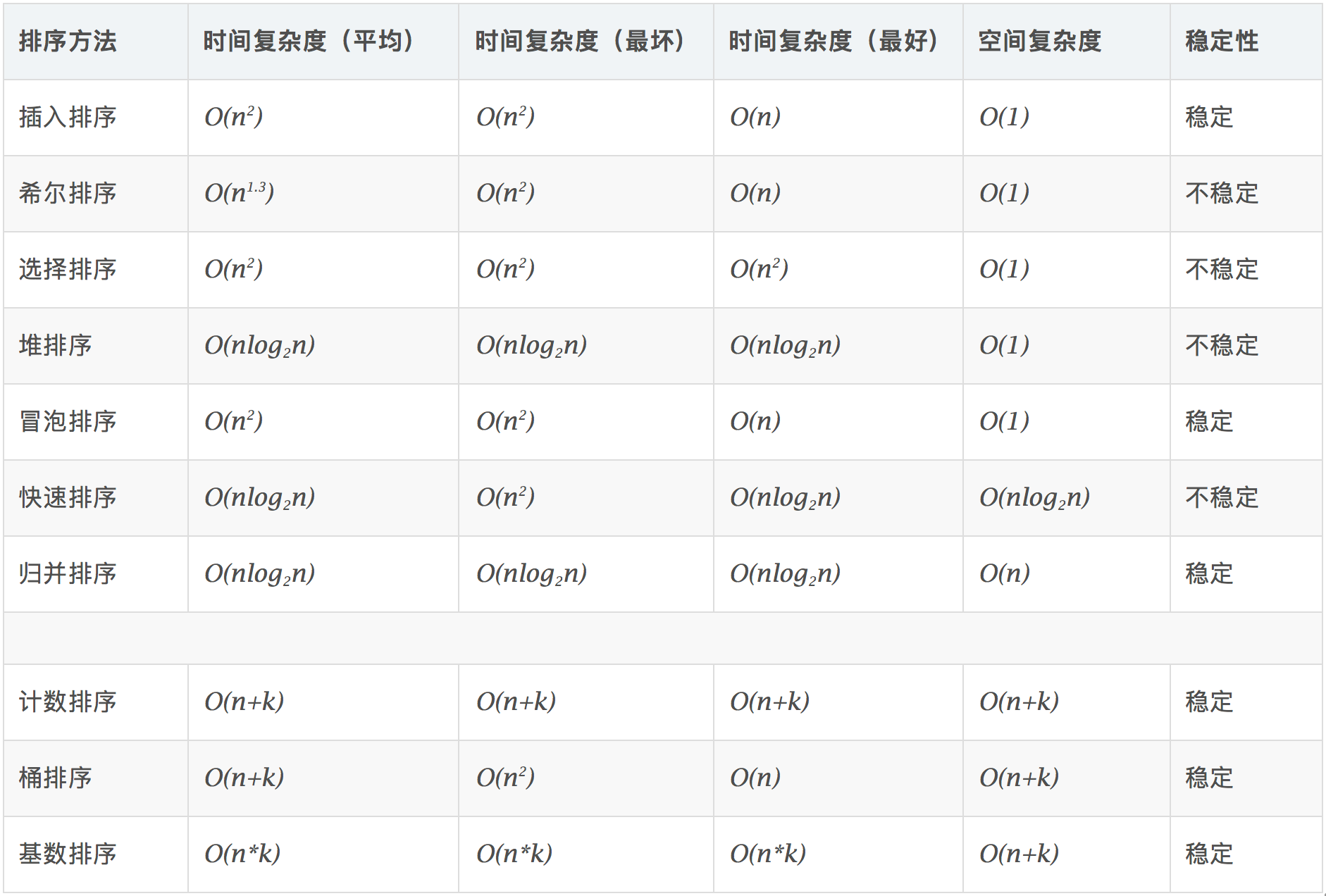
快排空间复杂度
1.插入排序
过程
从第一个元素开始,该元素可以认为已经被排序;
取出下一个元素,在已经排序的元素序列中从后向前扫描;
如果该元素(已排序)大于新元素,将该元素移到下一位置;
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
将新元素插入到该位置后;
重复步骤2~5。
我的话
前面有序,后面第一个数字去插前面的应该是它的位置,原来有序区插的位置之后的数字往后移。
为什么叫插入,因为是拿第一个数字去插前面的位置
2.希尔排序
过程
3.选择排序
过程
初始状态:无序区为R[1..n],有序区为空;
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
n-1趟结束,数组有序化了。
我的话
前面有序,后面无序去找出最小的数字放第一个(和原来的第一个交换),这个数字就变成有序区的了。
为什么叫选择,因为是要在无序区选出一个最小的数字
4.堆排序
过程
5.冒泡排序
过程
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
针对所有的元素重复以上的步骤,除了最后一个;
重复步骤1~3,直到排序完成。
我的话
从头开始一直比较相邻元素,比较完一趟最后一个数变成最大的,以此类推。
为什么叫冒泡呢?相邻元素比较重复=冒泡 就是硬记
6.快速排序
过程
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
我的话
随便选一个基准,左边比他小右边比他大,递归继续做左右两边
为什么叫快速呢? 快速=以标准划分分递归 感觉比简单算法高端 就叫快速
最好最坏分析
最好情况O(n*logn)——Partition函数每次恰好能均分序列,其递归树的深度就为.log2n.+1(.x.表示不大于x的最大整数),即仅需递归log2n次; 最坏情况O(n^2),每次划分只能将序列分为一个元素与其他元素两部分,这时的快速排序退化为冒泡排序,如果用数画出来,得到的将会是一棵单斜树,也就是说所有所有的节点只有左(右)节点的树;平均时间复杂度O(n*logn)
具体可以参考 https://blog.csdn.net/weixin_42109012/article/details/91645051
7.归并排序
过程
把长度为n的输入序列分成两个长度为n/2的子序列;
对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
我的话
和快速的区别就是二分递归
为什么叫归并呢?先分开,再归并,所以叫归并排序。
8.堆排序
过程
将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆(从大到小就是小顶堆),此堆为初始的无序区;
将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。

