判断点是否在三角形内

我个人常用的方法多为叉积法，而不是面积法。

原因很简单，相较来说叉积法速度会比面积法更快一些。（个人测，并不严谨）

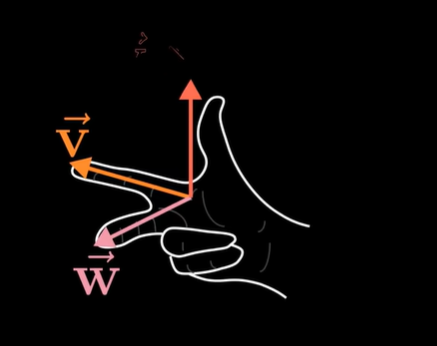
其实根据右手定则，我们很容易可以判断出点是否在三角形中，我们只需要判断点 是否 在三个 向量 的左侧即可；

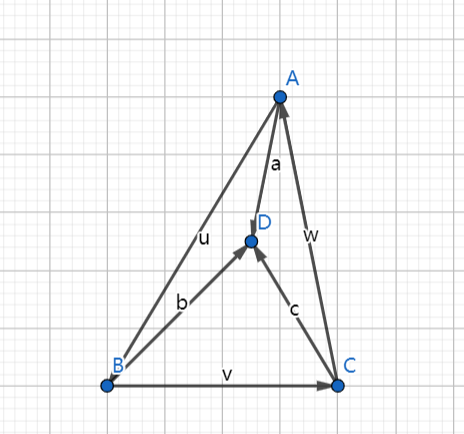
但在一开始，我们需要先判断三角形时候为逆时针，即点B是否在C的左侧。若不是交换位置（point变量名位置）

#include <iostream>

// 计算叉积的函数
int crossProduct(int x1, int y1, int x2, int y2) {
    return x1 * y2 - x2 * y1;
}

// 判断点是否在三角形内的函数
bool isInTri2(int x1, int y1, int x2, int y2, int x3, int y3, int x, int y) {
    // 确保三个点相对位置为逆时针方向：1 -> 2 -> 3
    if (crossProduct(x2 - x1, y2 - y1, x3 - x1, y3 - y1) >= 0) {
        std::swap(x2, x3);
        std::swap(y2, y3);
    }
    if (crossProduct(x2 - x1, y2 - y1, x - x1, y - y1) <= 0) {
        return false;
    }
    if (crossProduct(x3 - x2, y3 - y2, x - x2, y - y2) <= 0) {
        return false;
    }
    if (crossProduct(x1 - x3, y1 - y3, x - x3, y - y3) <= 0) {
        return false;
    }
    return true;
}

int main() {
    // 示例测试
    int x1 = 0, y1 = 0;
    int x2 = 5, y2 = 0;
    int x3 = 0, y3 = 5;
    int x = 2, y = 2;

    if (isInTri2(x1, y1, x2, y2, x3, y3, x, y)) {
        std::cout << "Point is inside the triangle." << std::endl;
    } else {
        std::cout << "Point is outside the triangle." << std::endl;
    }

    return 0;
}