Factorization Machine算法
参考:
http://stackbox.cn/2018-12-factorization-machine/
https://baijiahao.baidu.com/s?id=1641085157432717824&wfr=spider&for=pc
http://mini.eastday.com/mobile/171102132832769.html
http://ju.outofmemory.cn/entry/347921
Factorization Machine---因子分解机
Factorization Machine 主要目标是: 在数据稀疏的情况下解决组合特征的问题
作为一个2010年提出的模型, FM在工业界还依然有着很广泛的应用, 比如CTR预估, LearningToRank, 而且衍生出了DeepFM这种融合了深度学习的模型, FM模型的优点很明显 适用于CTR预估这种稀疏矩阵的情况 做好特征工程后就不用考虑组合特征了, 如果是在LR模型中添加组合特征, 则需要极其深刻的领域知识 在线上进行预测时候速度快, 模型训练也快。
FM (Factorization Machine) 算法可进行回归和二分类预测,它的特点是考虑了特征之间的相互作用,是一种非线性模型,目前FM算法是推荐领域被验证的效果较好的推荐方案之一,在诸多电商、广告、直播厂商的推荐领域有广泛应用。 PAI平台的FM算法基于阿里内部大数据的锤炼,具备性能优越、效果突出的特点。
因子分解法在很多预测问题上都有很好的准确性。但是分解模型运用在一个新的问题上并不是一个简单的事情。目前有很多的分解模型,最流行的应该是矩阵分解(Matrix Factorization, MF)。这是预测两个分类变量之间关系的模型。类似的,张量分解(Tensor Factorization,TF)是矩阵分解的扩展,它可以预测多个分类变量之间的关系,张量分解有很多例子,如Tucker Decomposition,Parallel Factor Analysis以及Pairwise Interaction Tensor Factorization等。除了分类变量,还有如SVD++、STE、FPMC、BPTF等等可以用来处理非分类的变量(这些模型都可以去原文找到对应的,基本上做矩阵分解的人应该都知道类似的原理大约是什么样子的)。作者列举了这么多方法的原因就是想说明,针对新的问题,我们总是需要设计新的模型来求解,这是很耗费时间的。因此,作者提出了一个新的模型,即分解机模型(Factorization Machine, FM),这是一个通用的方法,它可以通过特征工程来模仿大多数分解模型。据此,作者还提出了一个和LIBSVM很相似的通用的工具——LIBFM来帮助大家解决因子分解法的模型的应用。 本篇目录一、FM提出的原因 二、FM模型 三、FM模型的求解 3.1、FM优化的目标 3.2、FM的概率形式
FM的思想是将wij变成两个向量的乘积: 这里的kk就是我们在矩阵分解中常见的隐向量的维度。这个式子可以改写成: FM的参数是: 总共有1+n+nk个参数。从这些我们可以看出,FM有一些很好的特性,主要是线性特性。这点使得模型很容易求解。
Factorization Machines(FM) 因子分解机是Steffen Rendle于2010年提出,而Field-aware Factorization Machine (FFM) 场感知分解机最初的概念来自于Yu-Chin Juan与其比赛队员,它们借鉴了辣子Michael Jahrer的论文中field概念,提出了FM的升级版模型。 FM的paper中主要对比对象是SVM支持向量机,与SVM相比,有如下几个优势 FM可以实现对于输入数据是非常稀疏(比如自动推荐系统),而SVM会效果很差,因为训出的SVM模型会面临较高的bias。 FMs拥有线性的复杂度, 可以通过 primal 来优化而不依赖于像SVM的支持向量机。 在推荐系统和计算广告领域,点击率CTR(click-through rate)和转化率CVR(conversion rate)是衡量广告流量的两个关键指标。准确的估计CTR、CVR对于提高流量的价值,增加广告收入有重要的指导作用。FM和FFM近年来表现突出,分别在由Criteo和Avazu举办的CTR预测竞赛中夺得冠军。
从该矩阵中获取到特征的某些关联
FM总结 首先是为什么使用向量的点积可以解决以上问题呢? 参数的数量大幅度缩减,从n×(n−1)/2降低到nk 隐向量的点积可以表示原本两个毫无相关的参数之间的关系 而稀疏数据下学习不充分的问题也能得到充分解决。比如原本的多项式回归的参数[Math Processing Error]w12的学习只能依赖于特征[Math Processing Error]x1和[Math Processing Error]x2;而对参数[Math Processing Error]⟨v1,v2⟩而言就完全不一样了,它由[Math Processing Error]v1和[Math Processing Error]v2组成。而对于每个向量可以通过多个交叉组合特征学习得到,比如可以由[Math Processing Error]x1x2,x1x3,..学习获得,这样可供学习的非零样本就大大增加了。
Field-aware Factorization Machine(FFM) 场感知分解机 场感知说白了可以理解为分类。通过引入field的概念,FFM把相同性质的特征归于同一个field。比如, “MovieClass = romantic”、“MovieClass = action”这2个特征值都是代表电影分类的,可以放到同一个field中。简单来说,同一个类别的特征经过One-Hot编码生成的数值特征都可以放到同一个field。在FFM中,每一维特征 [Math Processing Error]xi,针对其它特征的每一种field [Math Processing Error]fj,都会学习一个隐向量 [Math Processing Error]vi,fj。因此,隐向量不仅与特征相关,也与field相关。也就是说,“MovieClass”这个特征与“UserRate”特征和“PlayTimes”特征进行关联的时候使用不同的隐向量,也是FFM中“field-aware”的由来。
FM(Factorization Machine)主要目标是:解决数据稀疏的情况下,特征怎样组合的问题。
因式分解机是一种基于LR模型的高效的学习特征间相互关系, 对于因子分解机FM来说,最大的特点是对于稀疏的数据具有很好的学习能力。
FM优点
① FMs allow parameter estimation under very sparse data where SVMs fails.(FM模型可以在非常稀疏的数据中进行合理的参数估计,而SVM做不到这点)
② FMs have linear complexity,can be optimized in the primal and do not rely on support vectors like SVMs. (在FM模型的复杂度是线性的,优化效果很好,而且不需要像SVM一样依赖于支持向量。)
③ FMs are a general predictor that can work with any real valued feature vector. In contrast to this, other state-of-the-art factorization models work only on very restricted input data. (FM是一个通用模型,它可以用于任何特征为实值的情况。而其他的因式分解模型只能用于一些输入数据比较固定的情况。)
在一般的线性模型中,是各个特征独立考虑的,没有考虑到特征与特征之间的相互关系。但实际上,大量的特征之间是有关联的。最简单的以电商为例,一般女性用户看化妆品服装之类的广告比较多,而男性更青睐各种球类装备。那很明显,女性这个特征与化妆品类服装类商品有很大的关联性,男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来,显然是很有意义的
FM算法:https://blog.csdn.net/g11d111/article/details/77430095
http://ju.outofmemory.cn/entry/347921
可以解决稀疏向量问题,因为每个特征都有一个隐向量,就算是稀疏向量在训练样本没有出现过的组合在预测时也可以进行计算 同时参数空间也降低到了$O(n\cdot k)$
FFM 其实是在 FM 的基础上做了一些更加细致化的工作:作者Yuchin认为相同性质的特征归于同一field,而当前特征在不同field上的表现应该是不同的. 比如在广告领域中性别对于广告商(Advertiser)和投放地(Publisher)的作用就是不一样的,
DeepFM 受到 Wide&Deep 的启发,Huifeng等人将FM和Deep深度学习结合了起来,简单的说就是将 Wide 部分使用 FM 来代替,同时FM的隐向量可以充当Feature的Embedding,非常巧妙:
DeepFM 的架构其实特别清晰: 输入的是稀疏特征的id 进行一层lookup 之后得到id的稠密embedding 这个embedding一方面作为隐向量输入到FM层进行计算 同时该embedding进行聚合之后输入到一个DNN模型(deep) 然后将FM层和DNN层的输入求和之后进行co-train
DeepFm 的非作者源码分享 https://github.com/ChenglongChen/tensorflow-DeepFM
而 AFM(Attentional Factorization Machines) 同样,是在 FM 上做了一些小 trick ,在传统的 FM 中进行特征组合时两两特征之间的组合都是等价的(只能通过隐向量的点积来区别),这里趁着 Attention 的热度走一波,因为 AFM 的最大的贡献就是通过 Attention 建立权重矩阵来学习两两向量组合时不同的权重。下面就是 AFM 的框架图:
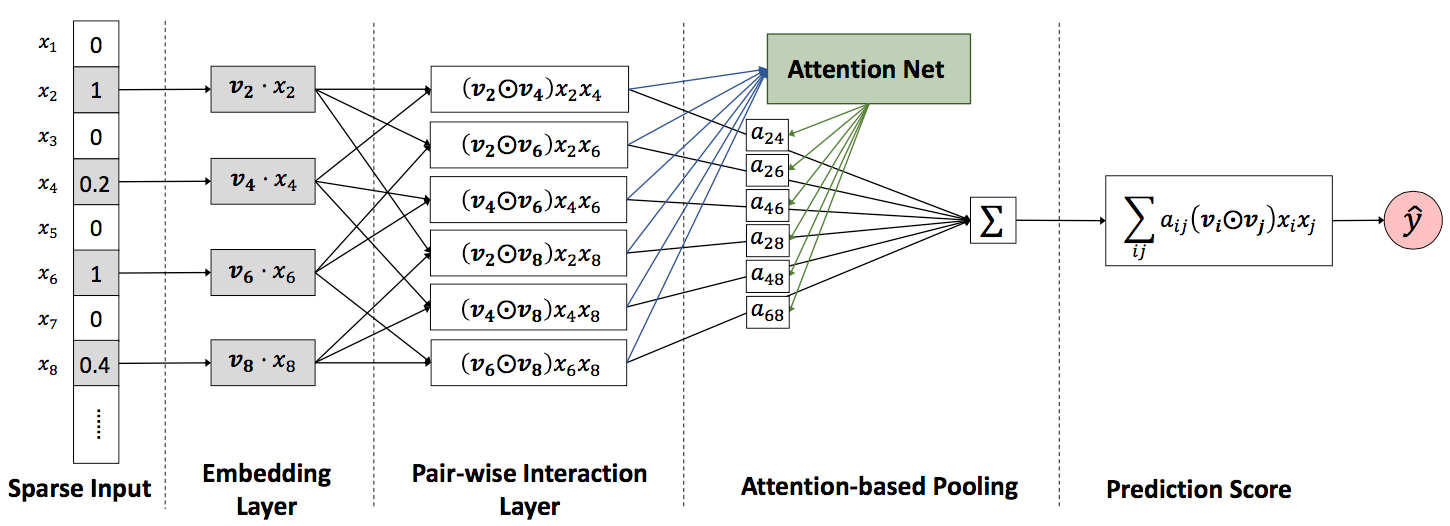
从图中可以很清晰的看出, AFM 比 FM 就是多了一层 Attention-based Pooling ,该层的作用是通过 Attention 机制生成一个$a_{i,j}$权重矩阵,该权重矩阵将会作用到最后的二阶项中,因此这里$a_{i,j}$的生成步骤是先通过原始的二阶点积求得各自的组合的一个score: $${a}’{i,j} = h^T \text{ReLu}(W(v_i \odot v_j)x_ix_j+b)$$ > 其中$W \in \mathbb{R}^{t \times k},b \in \mathbb{R}^t , h \in \mathbb{R}^t$,这里$t$表示 Attention 网络的大小 然后对其score进行 softmax 的归一化: $$a = \frac{exp({a}’{i,j})}{\sum exp({a}’{i,j})}$$ 最后该权重矩阵再次用于二阶项的计算(也就是最终的 AFM 式子): $$y{\text{AFM}}(x) = w_0+\sum_i^n w_i x_i + P^T \sum_{i=1}^n \sum_{j=i+1}^n a_{i,j} (v_i \odot v_j) x_ix_j$$ 其实整个算法思路也是很简单,但是在实验上却有一个不错的效果:
其实从实验效果来看 AFM 应该是优于 NFM AFM 的作者源码分享 https://github.com/hexiangnan/attentional_factorization_machine
总结 FMs 系列算法被广泛应用于ctr预估类的问题中,并且可以取得不错的效果,他最大特征是可以帮助解决特征组合问题 原始 FM 算法的运行性能最快,可以达到$O(k \bar{n})$,在工业中被适用最广最简单,其他带上神经网络的 FM 算法如果想在在线系统中使用得做很多离线计算和分解,比如 FFM 的现在复杂度是$O(k \bar{n}2)$,将$O(\bar{n}2)$中二阶计算的项尽可能的进行离线计算,在 在线的时候进行组合 FM 的二阶项部分很容易使用 TensorFlow 进行实现,这也意味了在实验上也很容易很其他复杂算法进行组合:

Factorization Machine---因子分解机:来自简书
https://www.baidu.com/link?url=Brgydqp_ehJeHkcheNmAxNLXPM3i6fY0X7in44ykcW6vC5fc10o2YjZap8v5Ky-g8CNIrfKKaPg2CZCv2l8oAg1RhWi5wD43aHQdedbWXny&wd=&eqid=b82a70f600007562000000035daacfbe
Factorization Machine的优点 ①对于一些很稀疏的数据集也可以进行参数的预测,而SVM是不行的。 ②FM有线性的复杂性,可以直接在原始数据进行预测,而不需要再做核函数或者特征转换,对于SVM,是要基于对支持向量的优化的。 ③FMs是一种通用的预测器,可用于任何实值特征向量。相比之下。其他最先进的因数分解模型只在非常有限的输入数据上工作。通过定义输入数据的特征向量,FMs可以模拟最先进的模型,如偏置MF、SVD++、PITF或FPMC。 K的选择 如果数据是一个稀疏矩阵,那么可以选择一个比较小的k,因为稀疏矩阵其实就已经表明这个矩阵的信息是十分有限的了,再取比较大的k可能会导致过拟合。如果数据并不是一个稀疏矩阵,可以选择大一点的k来代表数据。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号