GCN 简单numpy实现

`#参考：https://blog.csdn.net/weixin_42052081/article/details/89108966
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from networkx import to_numpy_matrix

#首先使用numpy编写有向图的邻接矩阵表征
A=np.matrix([[0,1,0,0],[0,0,1,1],[0,1,0,0],[1,0,1,0]],dtype=float)

#抽取特征，基于每个节点的索引为其生成两个整数特征
X=np.matrix([[i,-i] for i in range(A.shape[0])],dtype=float)
print(X)

#应用传播规则 ：现在我们已经建立了一个图，其邻接矩阵为A，输入特征的几何为X
# 接下来我们来看一下应用传播规则之后会发生什么
print(A*X)
#每个节点的表征（每一行）现在是其相邻节点特征的和！
# 换句话说，图卷积层将每个节点表示为其相邻节点的聚合。
# 大家可以自己动手验证这个计算过程。
# 请注意，在这种情况下，
# 如果存在从 v 到 n 的边，则节点 n 是节点 v 的邻居。

#问题
#以上的做法包含以下问题：
#1.节点的聚合表征不包含它自己的特征！该表征是相邻节点的特征聚合，因此只有具有自环（self-loop）
# 的节点才会在该聚合中包含自己的特征 [1]。
#2 2，度大的节点在其特征表征中将具有较大的值，
# 度小的节点将具有较小的值。这可能会导致梯度消失或梯度爆炸 [1, 2]，
# 也会影响随机梯度下降算法（随机梯度下降算法通常被用于训练这类网络，
# 且对每个输入特征的规模（或值的范围）都很敏感）。

#增加自环：为了解决第一个问题，可以在使用传播规则之前，先将A与单位矩阵I相加实现

I=np.matrix(np.eye(A.shape[0]))
A_hat=A+I
print("A_hat is :",A_hat)
print(A_hat*X)

#对特征表征进行归一化处理
#通过将邻接矩阵A与度矩阵D的逆相乘，对其进行变换，从而通过节点的度对特征表征进行归一化
#因此简化后的传播规则如下：
#F(X,A)=D^(-1)AX
# 首先计算出节点的度矩阵。注意：此处计算节点的度是用节点的入度，也可以根据自身的任务特点用出度，
# 在本文中，这个选择是任意的。一般来说，您应该考虑节点之间的关系是如何与您的具体任务相关。
# 例如，您可以使用in-degree来进行度矩阵计算，前提是只有关于节点的in-neighbors的信息与预测其具体任务中的标签相关。
# 相反，如果只有关于外部邻居的信息是相关的，则可以使用out-degree。最后，如果节点的out-和in-邻居都与您的预测相关，
# 那么您可以基于in-和out-度的组合来计算度矩阵。
# 正如我将在下一篇文章中讨论的那样，您还可以通过其他方法对表示进行归一化，而不是使用逆矩阵乘法。

#计算度矩阵
D=np.array(np.sum(A,axis=0))[0]
D=np.matrix(np.diag(D))
print(D)

#变化之前
A = np.matrix([     [0, 1, 0, 0],     [0, 0, 1, 1],      [0, 1, 0, 0],     [1, 0, 1, 0]],     dtype=float)

#变换之后
print(D**-1 * A)

# 可以观察到，邻接矩阵中每一行的权重（值）都除以该行对应节点的度。我们接下来对变换后的邻接矩阵应用传播规则：
# 得到与相邻节点的特征均值对应的节点表征。
# 这是因为（变换后）邻接矩阵的权重对应于相邻节点特征加权和的权重。大家可以自己动手验证这个结果。

# print(D**-1 * A*X)

#整合：现在将自环和归一化技巧结合起来，还将重新介绍之前为了简化讨论而省略的有关权重和激活函数的操作

#添加权重
# 这里的 D_hat 是 A_hat = A + I 对应的度矩阵，即具有强制自环的矩阵 A 的度矩阵。
D_hat=np.array(np.sum(A_hat,axis=0))[0]
D_hat=np.matrix(np.diag(D_hat))
print("D_hat is :",D_hat)

W = np.matrix([ [1, -1],
              [-1, 1] ])
print("Adding W：  ",D_hat**-1 * A_hat * X *W)

# 如果我们想要减小输出特征表征的维度，我们可以减小权重矩阵 W 的规模：
W = np.matrix([              [1],
                             [-1]          ])
print("After reducing the size of W：  ",D_hat**-1 * A_hat * X * W)

# 添加激活函数:  本文选择保持特征表征的维度，并应用 ReLU 激活函数。Relu函数的公式是，代码为：
def relu(x):
    return(abs(x)+x)/2

# 一个带有邻接矩阵、输入特征、权重和激活函数的完整隐藏层如下：

W = np.matrix([              [1, -1],
                             [-1, 1]          ])
print("After adding RELU :",relu(D_hat**-1 * A_hat * X * W))


#以下是在真实场景中的应用
# Zachary 空手道俱乐部  Zachary 空手道俱乐部是一个被广泛使用的社交网络，
# 其中的节点代表空手道俱乐部的成员，边代表成员之间的相互关系。
# 当年，Zachary 在研究空手道俱乐部的时候，管理员和教员发生了冲突，导致俱乐部一分为二。
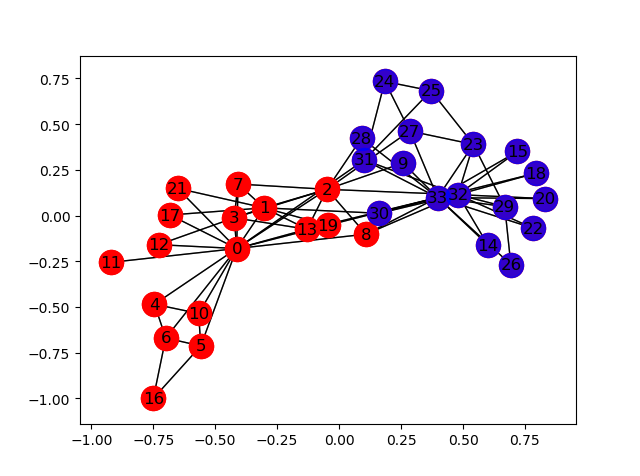
# 下图显示了该网络的图表征，其中的节点标注是根据节点属于俱乐部的哪个部分而得到的，
# 「0」表示属于Mr. Hi部分的中心节点，[32」表示属于Officer阵营的中心节点，
# 参考https://networkx.github.io/documentation/stable/_modules/networkx/generators/social.html#karate_club_graph。

zkc = nx.karate_club_graph()
def plot_graph(G):
    # G: a networkx G
    # % matplotlib notebook

    plt.figure()
    pos = nx.spring_layout(G)
    edges = G.edges()

    nodelist1 = []
    nodelist2 = []
    for i in range(34):
        if zkc.nodes[i]['club'] == 'Mr. Hi':
            nodelist1.append(i)
        else:
            nodelist2.append(i)
    nx.draw_networkx(G, pos, edges=edges);
    nx.draw_networkx_nodes(G, pos, nodelist=nodelist1, node_size=300, node_color='r', alpha=0.8)
    nx.draw_networkx_nodes(G, pos, nodelist=nodelist2, node_size=300, node_color='b', alpha=0.8)
    nx.draw_networkx_edges(G, pos, edgelist=edges,alpha =0.4)
    plt.show()

plot_graph(zkc)
#见图1

# #构建GCN，
# 构建一个图卷积网络。我们并不会真正训练该网络，但是会对其进行简单的随机初始化，从而生成我们在本文开头看到的特征表征。
# 我们将使用 networkx，它有一个可以很容易实现的 Zachary 空手道俱乐部的图表征。然后，我们将计算 A_hat 和 D_hat 矩阵。

from networkx import to_numpy_matrix
zkc = nx.karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)  #邻接矩阵
I = np.eye(zkc.number_of_nodes()) #单位矩阵
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]  #带自循环的度矩阵
D_hat = np.matrix(np.diag(D_hat))

#随机初始化权重
# np.random.normal()函数说明
#伟大的高斯分布（Gaussian Distribution）的概率密度函数（probability density function）：
# 对应于numpy中：numpy.random.normal(loc=0.0, scale=1.0, size=None)
# 参数的意义为：
# loc：float     此概率分布的均值（对应着整个分布的中心centre）
# scale：float     此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
# size：int or tuple of ints     输出的shape，默认为None，只输出一个值

W_1 =np.random.normal( loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
print("W_1 is :",W_1)

W_2 = np.random.normal(
    loc=0, size=(W_1.shape[1], 2))
print("W_2 is :",W_2)

# 接着堆叠 GCN 层。这里只使用单位矩阵作为特征表征，即每个节点被表示为一个 one-hot 编码的类别变量。

def gcn_layer(A_hat, D_hat, X, W):
    return relu(D_hat ** -1 * A_hat * X * W)
#relu 为激活函数

H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2
print(output)

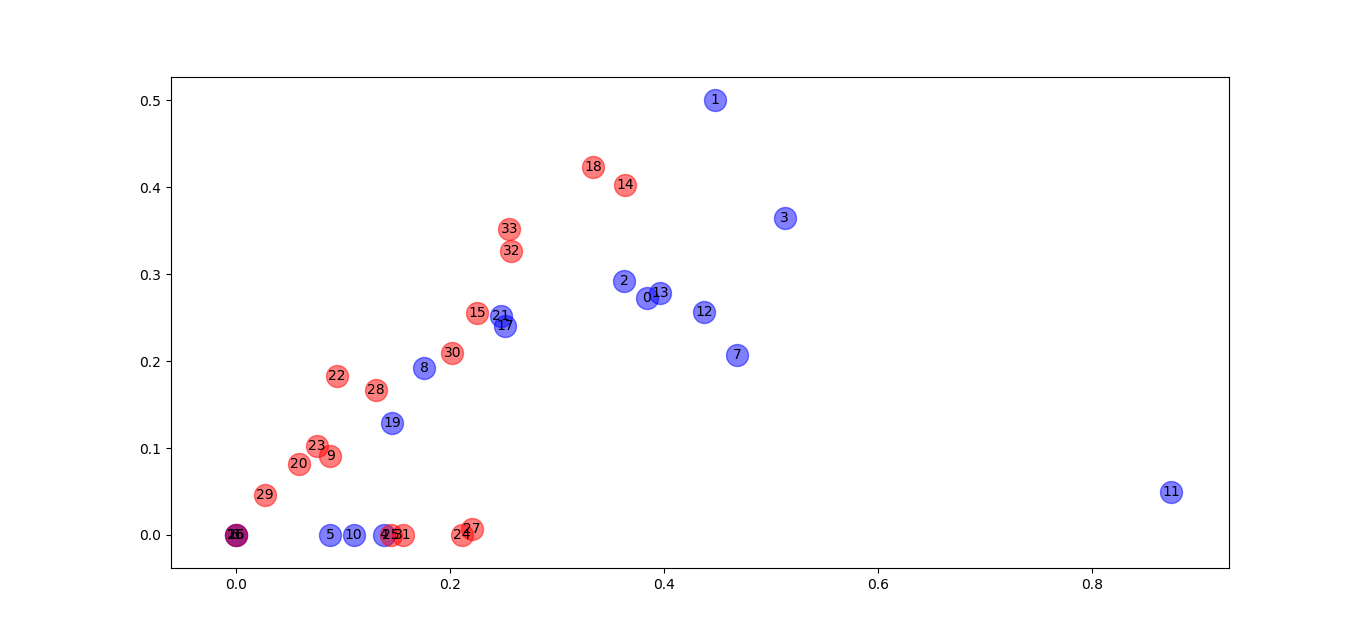
# 经过多次随机生成W_1和W_2权重矩阵，得到上图H_2，
# 但是我发现经过激活函数relu之后，x轴与y轴有很多零值，
# 导致可视化效果很差，可视化效果如下图，初步分析，可能的原因是权重矩阵是随机生成的，
# 没有用后面的具体任务去更新权重矩阵，，画图代码及图片如下：

# plt.scatter（） 散点图 https://blog.csdn.net/m0_37393514/article/details/81298503


for i in range (34):
    if zkc.nodes[i]['club'] == 'Mr. Hi':
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,label=str(i),color = 'b',alpha=0.5,s = 250)
        plt.text(np.array(output)[i,0],np.array(output)[i,1] ,i, horizontalalignment='center',verticalalignment='center', fontdict={'color':'black'})
        # 为每个点添加标签，一些形如（x轴，y轴，标签）的元组，水平及垂直位置，背景颜色
    else:
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,label = 'i',color = 'r',alpha=0.5,s = 250)
        plt.text(np.array(output)[i,0],np.array(output)[i,1] ,i, horizontalalignment='center',verticalalignment='center', fontdict={'color':'black'})
        # plt.scatter(np.array(output)[:,0],np.array(output)[:,1],label = 0:33)
print("The result of GCN is :")
plt.show()


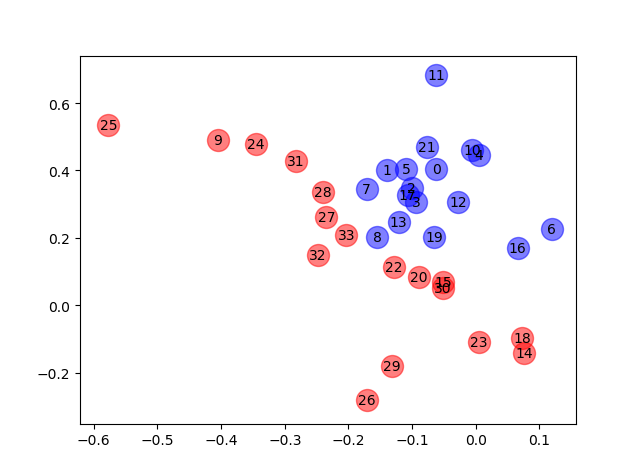
# 尝试去掉激活函数relu，重新运行一遍，发现效果反而更好
def gcn_layer(A_hat, D_hat, X, W):
    return D_hat**-1 * A_hat * X * W
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2
print("去掉relu :",output)


feature_representations = {
    node: np.array(output)[node]
    for node in zkc.nodes()}
print("feature_representations is :",feature_representations)

# import matplotlib.pyplot as plt
# %matplotlib notebook
for i in range (34):
    if zkc.nodes[i]['club'] == 'Mr. Hi':
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,label=str(i),color = 'b',alpha=0.5,s = 250)
        plt.text(np.array(output)[i,0],np.array(output)[i,1] ,i, horizontalalignment='center',verticalalignment='center', fontdict={'color':'black'})
        # 为每个点添加标签，一些形如（x轴，y轴，标签）的元组，水平及垂直位置，背景颜色
    else:
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,label = 'i',color = 'r',alpha=0.5,s = 250)
        plt.text(np.array(output)[i,0],np.array(output)[i,1] ,i, horizontalalignment='center',verticalalignment='center', fontdict={'color':'black'})
        # plt.scatter(np.array(output)[:,0],np.array(output)[:,1],label = 0:33)
plt.show()

# 你看，这样的特征表征可以很好地将 Zachary 空手道俱乐部的两个社区划分开来。
# 至此，我们甚至都没有开始训练模型！我们应该注意到，在该示例中由于 ReLU 函数的作用，
# 在 x 轴或 y 轴上随机初始化的权重很可能为 0。
# 结语  本文中对图卷积网络进行了高水平的的介绍，并说明了 GCN 中每一层节点的特征表征是如何基于其相邻节点的聚合构建的。
# 读者可以从中了解到如何使用 numpy 构建这些网络，以及它们的强大：
# 即使是随机初始化的 GCN 也可以将 Zachary 空手道俱乐部网络中的社区分离开来。 
#  在下一篇文章中，我将更详细地介绍技术细节，并展示如何使用半监督学习实现和训练最近发布的GCN。
# 你可以在本人csdn找到下一篇文章。

`

有激活函数的结果

去掉激活函数的结果