多任务学习Multi-task-learning MTL
https://blog.csdn.net/chanbo8205/article/details/84170813
多任务学习(Multitask learning)是迁移学习算法的一种,迁移学习可理解为定义一个一个源领域source domain和一个目标领域(target domain),在source domain学习,并把学习到的知识迁移到target domain,提升target domain的学习效果(performance)。
多任务学习(Multi-task learning):由于我们的关注点集中在单个任务上,我们忽略了可能帮助优化度量指标的其它信息。具体来说,这些信息来自相关任务的训练信号。通过共享相关任务之间的表征,可以使我们的模型更好地概括原始任务。这种方法被称为多任务学习(MTL)。其也是一种归纳迁移机制,主要目标是利用隐含在多个相关任务的训练信号中的特定领域信息来提高泛化能力,多任务学习通过使用共享表示并行训练多个任务来完成这一目标。归纳迁移是一种专注于将解决一个问题的知识应用到相关的问题的方法,从而提高学习的效率。比如,学习行走时掌握的能力可以帮助学会跑,学习识别椅子的知识可以用到识别桌子的学习,我们可以在相关的学习任务之间迁移通用的知识。此外,由于使用共享表示,多个任务同时进行预测时,减少了数据来源的数量以及整体模型参数的规模,使预测更加高效。因此,在多个应用领域中,可以利用多任务学习来提高效果或性能,比如垃圾邮件过滤、网页检索、自然语言处理、图像识别、语音识别等。
归纳偏执(inductive bias):归纳迁移的目标是利用额外的信息来源来提高当前任务的学习性能,包括提高泛化准确率、学习速度和学习的模型的可理解性。提供更强的归纳偏执是迁移提高泛化能力的一种方法,可以在固定的训练集上产生更好的泛化能力,或者减少达到同等性能水平所需要的训练样本数量。归纳偏执会导致一个归纳学习器更偏好一些假设,多任务学习正是利用隐含在相关任务训练信号中的信息作为一个归纳偏执来提高泛化能力。归纳偏置的作用就是用于指导学习算法如何在模型空间中进行搜索,搜索所得模型的性能优劣将直接受到归纳偏置的影响,而任何一个缺乏归纳偏置的学习系统都不可能进行有效的学习。不同的学习算法(如决策树,神经网络,支持向量机等)具有不同的归纳偏置,人们在解决实际问题时需要人工地确定采用何种学习算法,实际上也就是主观地选择了不同的归纳偏置策略。一个很直观的想法就是,是否可以将归纳偏置的确定过程也通过学习过程来自动地完成,也就是采用“学习如何去学(learning to learn)”的思想。多任务学习恰恰为上述思想的实现提供了一条可行途径,即利用相关任务中所包含的有用信息,为所关注任务的学习提供更强的归纳偏置。
由于我们的关注点集中在单个任务上,我们忽略了可能帮助优化度量指标的其它信息。具体来说,这些信息来自相关任务的训练信号。通过共享相关任务之间的表征,可以使我们的模型更好地概括原始任务。这种方法被称为多任务学习(MTL)。
MTL 有很多形式:联合学习(joint learning)、自主学习(learning to learn)和带有辅助任务的学习(learning with auxiliary task)等都可以指 MTL。一般来说,优化多个损失函数就等同于进行多任务学习(与单任务学习相反).
在深度学习中,多任务学习MTL通常通过隐藏层的 Hard 或 Soft 参数共享来完成。
Hard 参数共享
共享 Hard 参数是神经网络 MTL 最常用的方法,可以追溯到 [2]。在实际应用中,通常通过在所有任务之间共享隐藏层,同时保留几个特定任务的输出层来实现。
共享 Hard 参数大大降低了过拟合的风险。实际上,[3] 表明过拟合共享参数的风险为 O(N)——其中 N 是任务数——小于过拟合特定任务参数,即输出层。这很直观:我们同时学习的工作越多,我们的模型找到一个含有所有任务的表征就越困难,而过拟合我们原始任务的可能性就越小。
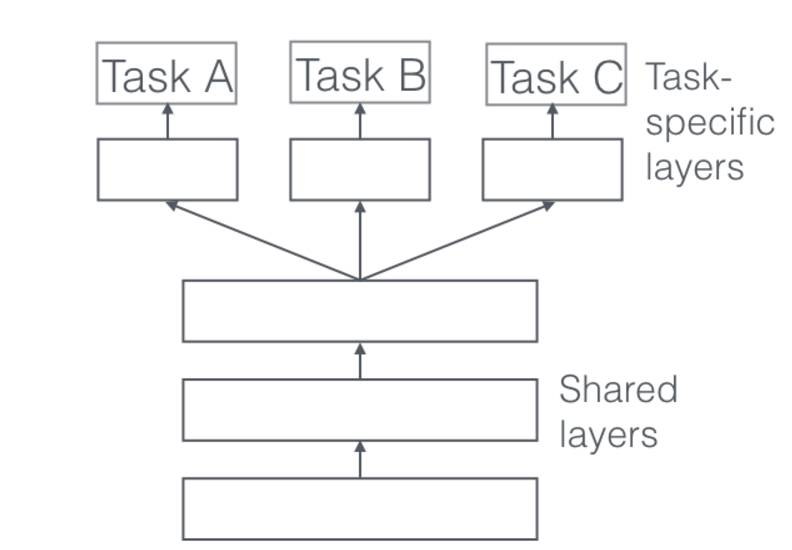
Soft 参数共享
另一方面,在共享 Soft 参数时,每个任务都有自己的参数和模型。模型参数之间的距离是正则化的,以便鼓励参数相似化。例如使用 L2 距离进行正则化 [4],而 [5] 使用迹范数(trace norm)。

约束深度神经网络 Soft 参数共享的思想受到了 MTL 正则化技术的极大启发,这种思想已经用于其它模型开发.
为什么 MTL 有效?
即使多任务学习获得的归纳偏置看起来是可信的,为了更好地了解 MTL,我们仍需要阐述它所基于的机制。其中大部分最初都是由 Caruana(1998)提出的。对于所有例子,假设我们有两个相关的任务 A 和 B,它们依赖于一个共同的隐藏层表征 F。
隐式数据增加
MTL 有效地增加了我们用于训练模型的样本大小。由于所有任务不同程度地存在噪声,当在某些任务 A 上训练模型时,我们的目标是为任务 A 学习一个很好的表征,理想情况下,这个表征能忽略与数据相关的噪声并具有良好的泛化性。由于不同的任务具有不同的噪声模式,所以同时学习两个任务的模型能够学习更一般的表征。只学习任务 A 有可能过拟合任务 A,而联合地学习 A 和 B 使模型能够通过平均噪声模式获得更好的表征。
注意力机制
如果一个任务非常嘈杂或数据量有限并且高维,模型可能难以区分相关与不相关的特征。MTL 可以帮助模型将注意力集中在重要的特征上,因为其它任务将为这些特征的相关性或不相关性提供额外的证据。
窃听(eavesdroping)
某特征 G 很容易被任务 B 学习,但是难以被另一个任务 A 学习。这可能是因为 A 以更复杂的方式与特征进行交互,或者因为其它特征阻碍了模型学习 G 的能力。通过 MTL,我们可以允许模型「窃听」,即通过任务 B 学习 G。最简单的方法是通过提示(hint)[6],即直接训练模型来预测最重要的特征。
表征偏置
MTL 任务偏好其它任务也偏好的表征,这造成模型偏差。这将有助于模型在将来泛化到新任务,因为在足够数量的训练任务上表现很好的假设空间也将很好地用于学习具有相同环境的新任务 [7]。
正则化
最后,MTL 通过引入归纳偏置作为正则化项。因此,它降低了过拟合的风险以及模型的 Rademacher 复杂度(即适合随机噪声的能力)。
非神经模型中的 MTL
为了更好地了解深度神经网络中的 MTL,我们将研究关于 MTL 在线性模型、核函数方法和贝叶斯算法方面的论文。特别地,我们将讨论一直以来在多任务学习的历史中普遍存在的两个主要思想:通过范数正则化制造各任务间的稀疏性;对任务间的关系进行建模。 请注意,许多 MTL 的论文具有同构性假设:它们假设所有任务与单个输出相关,例如,多类 MNIST 数据集通常被转换为 10 个二进制分类任务。最近的方法更加接近实际,对问题进行异构性假设,即每个任务对应于一组唯一的输出。
块稀疏(block-sparse)正则化
许多现有的方法对模型的参数做了稀疏性假设。例如,假设所有模型共享一小组特征 [8]。对我们任务的参数矩阵 A 来说,这意味着除了几行之外,所有数据都是 0,对应于所有任务只共同使用几个特性。为了实现这一点,他们将 L1 范数推广到 MTL。回想一下,L1 范数是对参数之和的约束,这迫使除几个参数之外的所有参数都为 0。这也被称为 lasso(最小绝对收缩与选择算子)。
可以看到,根据我们希望对每一行的约束,我们可以使用不同的 Lq。一般来说,我们将这些混合范数约束称为 L1/Lq 范数,也被称为块稀疏正则化,因为它们导致 A 的整行被设置为 0。[9] 使用 L1/L∞ 正则化,而 Argyriou 等人(2007)使用混合的 L1/L2 范数。后者也被称为组合 lasso(group lasso),最早由 [10] 提出。 Argyriou 等人(2007)也表明,优化非凸组合 lasso 的问题可以通过惩罚 A 的迹范数(trace norm)来转化成凸问题,这迫使 A 变成低秩(low-rank),从而约束列参数向量 a_{.,1},...,a_{.,t} 在低维子空间中。[11] 进一步使用组合 lasso 在多任务学习中建立上限。 尽管这种块稀疏正则化直观上似乎是可信的,但它非常依赖于任务间共享特征的程度。[12] 显示,如果特征不重叠太多,则 Ll/Lq 正则化可能实际上会比元素一般(element-wise)的 L1 正则化更差。 因此,[13] 通过提出一种组合了块稀疏和元素一般的稀疏(element-wise sparse)正则化的方法来改进块稀疏模型。他们将任务参数矩阵 A 分解为两个矩阵 B 和 S,其中 A=B+S。然后使用 L1/L∞ 正则化强制 B 为块稀疏,而使用 lasso 使 S 成为元素一般的稀疏。最近,[14] 提出了组合稀疏正则化的分布式版本。
学习任务的关系
尽管组合稀疏约束迫使我们的模型仅考虑几个特征,但这些特征大部分用于所有任务。所有之前的方法都基于假设:多任务学习的任务是紧密相关的。但是,不可能每个任务都与所有任务紧密相关。在这些情况下,与无关任务共享信息可能会伤害模型的性能,这种现象称为负迁移(negative transfer)。 与稀疏性不同,我们希望利用先验信息,指出相关任务和不相关任务。在这种情况下,一个能迫使任务聚类的约束可能更适合。[15] 建议通过惩罚任务列向量 a_{.,1},...,a_{.,t} 的范数与它们具有以下约束形式的方差来强加聚类约束:
深度关系网络
在用于计算机视觉的 MTL 中,通常的方法是共享卷积层,同时学习特定任务的全连接层。[34] 通过提出深度关系网络(Deep Relationship Network)来改进这些模型。除了图 3 中可以看到的共享和特定任务层的结构之外,他们在全连接层上使用矩阵先验(matrix priors),这样可以让模型学习任务之间的关系,类似于一些之前看过的贝叶斯模型。然而,这种方法仍然依赖于预定义的共享结构,这可能对于已经充分研究的计算机视觉问题是可行的,但是其证明对于新任务来说容易出错。
加权损失与不确定性
与学习共享的结构不同,[39] 通过考虑每个任务的不确定性应用正交方法(orthogonal approach)。然后,他们通过基于最大化任务决定的不确定性的高斯似然估计,求导多任务损失函数,并以此来调整成本函数中的每个任务的相对权重。每一像素的深度回归(per-pixel depth regression)、语义和实例分割的架构可以在图 7 中看到。
机器视觉领域有广泛的多任务学习应用,主要方式包括:
多个任务并行输出; 同时做分类和回归或使用不同的损失函数; 多个任务如流水线般,辅助任务附加在主任务后面。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号