基于移动最小二乘的图像变形和曲线拟合

在最近的项目中经常遇到给出几个点需要拟合出一条曲线。

在离散的点云中，求曲线曲面拟合，不能简单地连接这些点，如果知道曲线曲面的形式，如为二次曲线等，可以简单地使用最小二乘法估计参数；但如果曲线曲面形式未知，可以使用移动最小二乘法或者主曲线方法。

转载：https://blog.csdn.net/liumangmao1314/article/details/54179526

MLS的讲解

移动最小二乘法是在最小二乘法基础上加以改进的，添加了权函数等，具体的可以参考论文，“移动最小二乘法论文”链接，这篇论文对MLS讲解的很详细，最后还给出了程序设计思路。

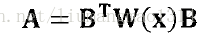
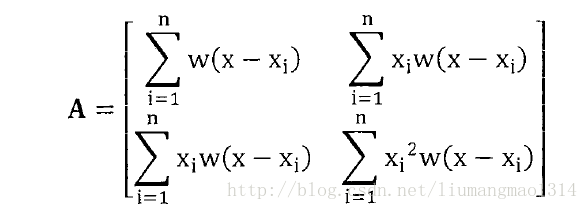
我做一点点说明，论文中的矩阵A的写法欠妥，其他关于移动最小二乘法研究中还有另外一种写法：，这里的B对应论文中的P，这点要注意，这样的话A就是一个矩阵。如果是线性基的二维曲线，矩阵A就是： 

，依次类推，其他的可以详看论文。

MLS代码块

代码的话我是根据论文中提供的程序设计，再结合一些网上的资料编写出来的，编程语言是C++；当然我也编写了python，应该是先编python，再编的C++。原因是python中可以加载一个矩阵运算库，C++中没有矩阵运算，要自己编写库，大家可以参考我这篇博客，介绍了矩阵运算链接。但是后来实验发现，python跑起来很费时间，C++只需它的一半的时间久跑完了，需要python代码也可以私信我，这里就不贴了。哦，对了，代码是包含很多自定义函数和变量，大家不要瞎贴代码，对照那篇论文的程序设计思路一下子就懂了，话不多说，上代码：

//移动最小二乘法的具体计算过程，参照论文“基于移动最小二乘法的曲线曲面拟合”，AB矩阵参照论文“移动最小二乘法的研究”
int MLS_Calc(int x_val,int y_val,float x[],float y[],float z[])
{
    int max_delta=max_x-min_x;//区域半径
    float p[M][N]={0};
    float sumf[N][N]={0};
    float w[M]={0};
    for(int j=0;j<M;j++)//求w
    {
        float s=fabs((x[j]-x_val))/max_delta;
        if(s<=0.5)
            w[j]=2/3.0-4*s*s+4*s*s*s;
        else
        {
            if(s<=1)
                w[j]=4/3.0-4*s+4*s*s-4*s*s*s/3.0;
            else
                w[j]=0;
        }
        p[j][0]=1;//每个采样点计算基函数
        p[j][1]=x[j];
        p[j][2]=y[j];
        p[j][3]=x[j]*x[j];
        p[j][4]=x[j]*y[j];
        p[j][5]=y[j]*y[j];
    }
    f(w,x,y,sumf,p);//计算得出A矩阵

    float p1[N];
    Matrix A=Trans_Matrix(sumf,N);
    Matrix A_1=m_c.Matrix_copy(&A);
    m_c.Matrix_inv(&A_1);//求A矩阵的逆A_1

    Matrix B(N,1);//求矩阵B，N行M列
    B.init_Matrix();
    for(int j=0;j<M;j++)//求得B矩阵的每列
    {
        p1[0]=1*w[j];
        p1[1]=x[j]*w[j];
        p1[2]=y[j]*w[j];
        p1[3]=x[j]*x[j]*w[j];
        p1[4]=x[j]*y[j]*w[j];
        p1[5]=y[j]*y[j]*w[j];
        Matrix P=Trans_Matrix_One(p1,N);//数组P1转成1行N列的P矩阵
        if(j==0)//第一列直接赋值
        {
            for(int i=0;i<N;i++)
                B.write(i,0,p1[i]);
        }
        else
        {
            m_c.Matrix_trans(&P);//矩阵转置，P转为N行1列矩阵
            m_c.Matrix_addCols(&B,&P);//矩阵B列附加，形成N行M列矩阵
        }
        P.free_Matrix();
    }

    float D[N]={1,x_val,y_val,x_val*x_val,x_val*y_val,y_val*y_val};
    Matrix D1=Trans_Matrix_One(D,N);//转成1行N列矩阵

    Matrix D_A1_mul(1,N);//定义矩阵并初始化相乘的结果矩阵，1行N列
    D_A1_mul.init_Matrix();
    if(m_c.Matrix_mul(&D1,&A_1,&D_A1_mul)==-1)
        cout<<"矩阵有误1！";//1行N列矩阵乘以N行N列矩阵得到结果为1行N列

    Matrix D_A1_B_mul(1,M);//定义矩阵并初始化相乘的结果矩阵，1行M列
    D_A1_B_mul.init_Matrix();
    if(m_c.Matrix_mul(&D_A1_mul,&B,&D_A1_B_mul)==-1)
        cout<<"矩阵有误2";//1行N列矩阵乘以N行M列矩阵得到记过矩阵为1行M列

    Matrix z1=Trans_Matrix_One(z,M);//将数组z转换成1行M列矩阵
    m_c.Matrix_trans(&z1);//转置得到M行1列矩阵
    Matrix Z(1,1);//得到矩阵结果，1行1列
    Z.init_Matrix();
    if(m_c.Matrix_mul(&D_A1_B_mul,&z1,&Z)==-1)
        cout<<"矩阵有误3！";//1行M列矩阵乘以M行1列矩阵得到1行1列矩阵，即值Z

    float z_val=Z.read(0,0);
    if(z_val>255)
        z_val=255;
    if(z_val<0)
        z_val=0;

    A.free_Matrix();
    A_1.free_Matrix();
    B.free_Matrix();

    D1.free_Matrix();
    D_A1_mul.free_Matrix();
    D_A1_B_mul.free_Matrix();
    z1.free_Matrix();
    Z.free_Matrix();

    return (int)z_val;
}