OpenGL ES着色器语言之操作数（官方文档第五章）

5.1操作数

OpenGL ES着色器语言包含如下操作符.

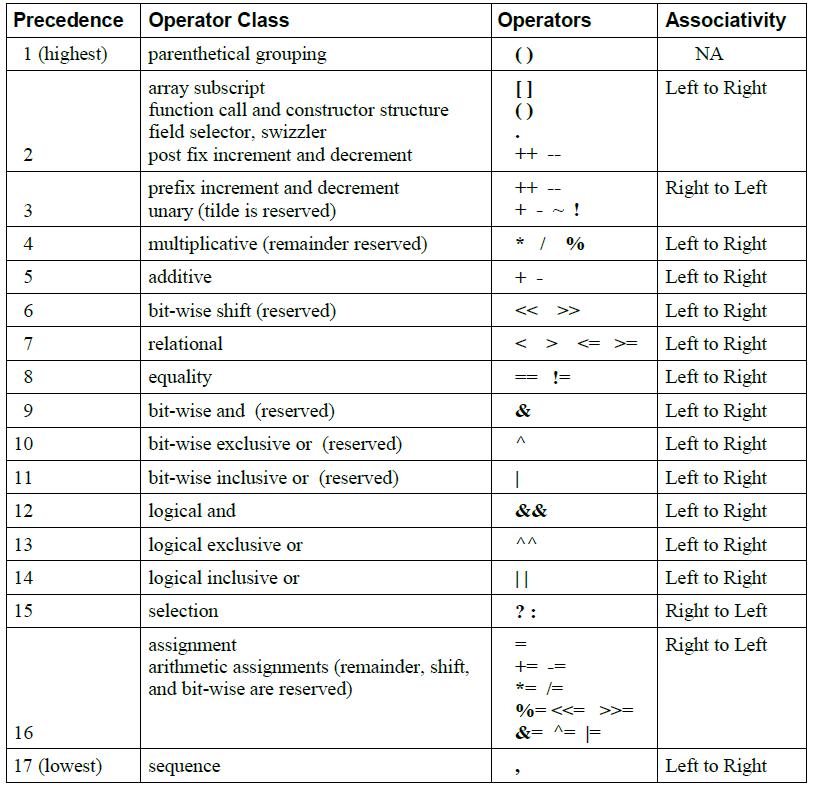
5.2数组下标

数组元素通过数组下标操作符([ ])进行访问.这是操作数组的唯一操作符,举个访问数组元素的例子:

diffuseColor += lightIntensity[3] * NdotL;

5.3函数调用

如果一个函数有返回值,那么通常这个函数调用会用在表达式中.

5.4构造器

构造器使用函数调用语法,函数名是一个基本类型的关键字或者结构体名字,在初始化器或表达式中使用.参数被用来初始化要构造的值.构造器可以将一个数据标量类型转换为另一个标量类型,或者从较小的类型转换为较大的类型,或者从较大的类型转为较小的类型.

5.4.1 转换和标量构造器

标量之间转换:

int (bool)         //将布尔型值转换成整数

int (float)         //将浮点数值转换成整数

float (bool)         //将布尔型值转换成浮点数

float(int)         //将整型值转换成浮点数

bool(int)         //将整数值转换成布尔型值

bool(float)         //将浮点数值转换成布尔型值

当构造器将一个float转换成int时,浮点数的小数部分将被自动舍弃掉.

当int和float转换成bool时,0和0.0被转换成false,非0值将被转换成true.当构造器将bool值转换成int或float时,false被转换成0或0.0, true被转换成1或1.0.

等价构造器,如float(float)也是合法的,但很少使用到.

如果构造器的参数不是标量,如向量,那么构造器将取其第一个元素.如float (vec3)构造器将取vec3中的第一个值.

5.4.2向量和矩阵构造器

构造器也可以用来从标量集合,向量,矩阵中创建向量和矩阵.同时可以缩短向量长度.

如果使用一个单一的标量来初始化向量,那么向量的所有值均使用该值进行初始化.如果使用一个单一的标量来初始化矩阵,那么矩阵的对角线的所有元素均会被初始化为该值,但其他元素将会被初始化为0.0

如果一个向量通过多个标量,向量或矩阵或这几种的混合来构造,那么向量的元素将按照参数列表的顺序来初始化.构造器将从参数列表中按从左到右的顺序去取参数,如果参数有多个值,那么再依次从这个参数中将值取出.构造矩阵也是类似的.矩阵元素将按照列为主要顺序来构造.构造器将依次从参数列表中取出参数值来构造矩阵的元素.如果参数列表中的值的个数超过矩阵或向量的元素个数的话,将会引起错误.

如果使用一个矩阵来构造矩阵的话,那么,参数矩阵中的元素值将放置到新矩阵的相应位置.

如果基本类型(int , float, bool)作为参数传进构造器,但是要构造的元素类型和传进来的数据类型不同,那么将会使用类型转换.

vec3(float) // initializes each component of with the float
vec4(ivec4) // makes a vec4 with component-wise conversion
vec2(float, float) // initializes a vec2 with 2 floats
ivec3(int, int, int) // initializes an ivec3 with 3 ints
bvec4(int, int, float, float) // uses 4 Boolean conversions
vec2(vec3) // drops the third component of a vec3
vec3(vec4) // drops the fourth component of a vec4
vec3(vec2, float) // vec3.x = vec2.x, vec3.y = vec2.y, vec3.z = float
vec3(float, vec2) // vec3.x = float, vec3.y = vec2.x, vec3.z = vec2.y
vec4(vec3, float)
vec4(float, vec3)
vec4(vec2, vec2)

 

vec4 color = vec4(0.0, 1.0, 0.0, 1.0);
vec4 rgba = vec4(1.0); // sets each component to 1.0
vec3 rgb = vec3(color); // drop the 4th component

 


mat2(float)
mat3(float)
mat4(float)


mat2(vec2, vec2);
mat3(vec3, vec3, vec3);
mat4(vec4, vec4, vec4, vec4);
mat2(float, float,
float, float);
mat3(float, float, float,
float, float, float,
float, float, float);
mat4(float, float, float, float,
float, float, float, float,
float, float, float, float,
float, float, float, float);

5.4.3结构体构造器

一旦结构体被定义,并给了一个类型名,那么和其同名的构造器就可以使用了.

struct light {
float intensity;
vec3 position;
};
light lightVar = light(3.0, vec3(1.0, 2.0, 3.0));

传进构造器的参数必须和结构体里面声明的具有相同的顺序和类型.

结构体构造器可以用于初始化器或者用在表达式中.

5.5向量组件

向量中每个组件的名称都使用一个单独的字符来表示.常用的位置,颜色,或者纹理坐标向量的组件直接和几个便利的数字相关联.访问向量中的组件可以使用向量名(.)组件名的方式.

支持的组件名称如下:

组件名称x,r,s在向量中是表示同一个组件的同义词.

注意,为了不和颜色向量中的r(红色)混淆,纹理向量中的第三个组件名称使用了p.

访问超出向量个数的组件会引起错误:

vec2 pos;
pos.x // is legal
pos.z // is illegal

组件选择语法可以一次选择多个组件:

vec4 v4;
v4.rgba; // is a vec4 and the same as just using v4,
v4.rgb; // is a vec3,
v4.b; // is a float,
v4.xy; // is a vec2,
v4.xgba; // is illegal - the component names do not come from
// the same set.

通过移动和替换组件可以产生不同的向量:

vec4 pos = vec4(1.0, 2.0, 3.0, 4.0);
vec4 swiz= pos.wzyx; // swiz = (4.0, 3.0, 2.0, 1.0)
vec4 dup = pos.xxyy; // dup = (1.0, 1.0, 2.0, 2.0)

组件组符号可以出现在左值中,也可以出现在右值中.

vec4 pos = vec4(1.0, 2.0, 3.0, 4.0);
pos.xw = vec2(5.0, 6.0); // pos = (5.0, 2.0, 3.0, 6.0)
pos.wx = vec2(7.0, 8.0); // pos = (8.0, 2.0, 3.0, 7.0)
pos.xx = vec2(3.0, 4.0); // illegal - 'x' used twice
pos.xy = vec3(1.0, 2.0, 3.0); // illegal - mismatch between vec2 and vec3

数组下标索引语法同样适用于向量.所以:

vec4 pos;

中pos[2]表示第三个元素，与使用pos.z是等价的。

5.6 矩阵组件

访问矩阵组件可以使用数组的下标索引语法。使用一维数组访问矩阵表示你要访问矩阵中对应的那一列组件，即返回相应列所有元素的向量。二位数组才是具体的访问某一个组件。由于矩阵是列优先的，因此，使用数组来索引矩阵元素的时候，数组的第一维表示列，第二维表示行。

mat4 m;
m[1] = vec4(2.0); // sets the second column to all 2.0
m[0][0] = 1.0; // sets the upper left element to 1.0
m[2][3] = 2.0; // sets the 4th element of the third column to 2.0

如果下标越界，将引起编译时错误。

5.7结构体和字段

结构体字段的访问也是要用到点操作符的（.）。

可用于结构体的操作有如下几种：

等于和赋值运算符只有两个操作数类型是同一个结构体时才有意义。即使两个结构体的名称和字段一模一样，他们也不是相等的。包含矩阵和采样器类型的结构体的赋值和等于操作是未定义的。

Struct S {int x;};
S a;
{
struct S {int x;};
S b;
a = b; // error: type mismatch
}

5.8 赋值

赋值表达式结构如下：

lvalue-expression = expression;

lvalue-expression 表示左值表达式，通过赋值运算符“=”将expression表达式的值赋给lvalue-expression；表达式和左值拥有相同的类型才会编译。所有的类型转换都必须显示地通过构造器来指定。左值必须是可写的。

支持 += 、 -= 、 *= 、 /=等运算符。

保留 %= 、<<= 、 >>=、 |=和^=等运算符以便后面修订用。

读取一个未被写入或初始化的变量是合法的，但其值是未定义的。

5.9 表达式

在着色语言中表达式由以下方式创建：

bool. int, float型常量，所有向量类型，所有矩阵类型。
所有类型的构造器
所有类型的变量名，除了不跟下标的数组名外
带下标的数组名
不带下标的数组名。一般只用在函数参数传递中。
带返回值的函数调用。
组件字段选择器和数组下标返回值。
括号表达式。任何表达式都可以是括号表达式。
二进制运算符 + 、 - 、 * 、 /
％保留修订用
一元负操作符（－），自加（＋＋），自减（－－）操作符。
比较运算符。大于（＞），小于（＜），大于等于（＞＝），小于等于（＜＝）。如果想比较向量，使用内建函数lessThan,lessThanEqual,greaterThan,greaterThanEqual。
等于（=）和不等于（！=）运算符。除了数组，包含数组的结构体，采样器，包含采样器的结构体外其他类型都可以使用。如果想让组件按位比较，使用内建的函数equal和notEqual。
逻辑二进制运算符（&&， ||， ^）。
逻辑一元运算符非（！）
逗号运算符。逗号运算符返回表达式序列中最后一个的结果。
三元选择运算符（？：）
运算符（＆，｜，＾，～，＞＞，＜＜）保留修订用。

5.10 常量表达式

　　常量表达式可以是以下几种：

字符值（如5或true）
全局或本地使用const修饰的变量，函数参数除外
返回常量数组，常量矩阵的某个元素或常量结构体的某个字段
参数都是常量表达式的结构体
所有参数都是常量表达式的内建函数类型，除了纹理查找函数外。

　　以下不能用在常量表达式：

用户自定义的函数
uniform,attribute,varying变量

　　数组变量不能使常量表达式，因为常量必须在声明时进行初始化，但是数组没有初始化机制

5.11 向量和矩阵操作

对矩阵和向量操作就是对向量和矩阵的每一个单独组建进行操作。举个例子

（１）向量和一个浮点数或整数相加，结果是向量的每一个元素都和该浮点数相加

vec3 v, u;
float f;
v = u + f;
等价于:
v.x = u.x + f;
v.y = u.y + f;
v.z = u.z + f;

（２）向量和向量相加，结果是两个向量的对应位置的组件分别相加

vec3 v, u, w;
w = v + u;

等价于：

w.x = v.x + u.x;
w.y = v.y + u.y;
w.z = v.z + u.z;

　这对于大部分操作符和所有的整数、浮点数向量和矩阵类型都是类似的操作。例外是矩阵和向量的乘法，矩阵和矩阵的乘法。如：

（３）向量乘以矩阵，结果是

vec3 v, u;
mat3 m;
u = v * m;
等价于：
u.x = dot(v, m[0]); // m[0] is the left column of m
u.y = dot(v, m[1]); // dot(a,b) is the inner (dot) product of a and b
u.z = dot(v, m[2]);

（４）矩阵乘以向量，结果是矩阵的各行和向量相乘
u = m * v;
等价于：
u.x = m[0].x * v.x + m[1].x * v.y + m[2].x * v.z;
u.y = m[0].y * v.x + m[1].y * v.y + m[2].y * v.z;
u.z = m[0].z * v.x + m[1].z * v.y + m[2].z * v.z;

（５）矩阵乘以矩阵，前一个矩阵的行乘以后一个矩阵的列
mat m, n, r;
r = m * n;
等价于：
r[0].x = m[0].x * n[0].x + m[1].x * n[0].y + m[2].x * n[0].z;
r[1].x = m[0].x * n[1].x + m[1].x * n[1].y + m[2].x * n[1].z;
r[2].x = m[0].x * n[2].x + m[1].x * n[2].y + m[2].x * n[2].z;
r[0].y = m[0].y * n[0].x + m[1].y * n[0].y + m[2].y * n[0].z;
r[1].y = m[0].y * n[1].x + m[1].y * n[1].y + m[2].y * n[1].z;
r[2].y = m[0].y * n[2].x + m[1].y * n[2].y + m[2].y * n[2].z;
r[0].z = m[0].z * n[0].x + m[1].z * n[0].y + m[2].z * n[0].z;
r[1].z = m[0].z * n[1].x + m[1].z * n[1].y + m[2].z * n[1].z;
r[2].z = m[0].z * n[2].x + m[1].z * n[2].y + m[2].z * n[2].z;

posted @ 2015-11-02 17:45 Anita-ff 阅读(313) 评论(0) 编辑收藏举报

刷新页面返回顶部

Anita-ff 的图像处理之旅

转行做了两年VR AR，现在又跑回来做图像＋AI了

OpenGL ES着色器语言之操作数（官方文档第五章）

OpenGL ES着色器语言之操作数（官方文档第五章）

5.1操作数

5.2数组下标

5.3函数调用

5.4构造器

5.4.1 转换和标量构造器

5.4.2向量和矩阵构造器

5.4.3结构体构造器

5.5向量组件

5.6 矩阵组件

5.7结构体和字段

5.8 赋值

5.9 表达式

5.10 常量表达式

公告