OpenGL------三维变换
我们生活在一个三维的世界——如果要观察一个物体,我们可以:
1、从不同的位置去观察它。(视图变换)
2、移动或者旋转它,当然了,如果它只是计算机里面的物体,我们还可以放大或缩小它。(模型变换)
3、如果把物体画下来,我们可以选择:是否需要一种“近大远小”的透视效果。另外,我们可能只希望看到物体的一部分,而不是全部(剪裁)。(投影变换)
4、我们可能希望把整个看到的图形画下来,但它只占据纸张的一部分,而不是全部。(视口变换)
这些,都可以在OpenGL中实现。
OpenGL变换实际上是通过矩阵乘法来实现。无论是移动、旋转还是缩放大小,都是通过在当前矩阵的基础上乘以一个新的矩阵来达到目的。OpenGL可以在最底层直接操作矩阵,不过作为初学,这样做的意义并不大。这里就不做介绍了。
1、模型变换和视图变换
从“相对移动”的观点来看,改变观察点的位置与方向和改变物体本身的位置与方向具有等效性。在OpenGL中,实现这两种功能甚至使用的是同样的函数。
由于模型和视图的变换都通过矩阵运算来实现,在进行变换前,应先设置当前操作的矩阵为“模型视图矩阵”。设置的方法是以GL_MODELVIEW为参数调用glMatrixMode函数,像这样:
glMatrixMode(GL_MODELVIEW); //需要修改的是模型视图矩阵、投影矩阵还是纹理矩阵。mode的值可以为:GL_MODELVIEW、GL_PROJECTION或GL_TEXTURE。
通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。这也只需要一行代码:
glLoadIdentity();
然后,就可以进行模型变换和视图变换了。进行模型和视图变换,主要涉及到三个函数:
glTranslate*,把当前矩阵和一个表示移动物体的矩阵相乘。三个参数分别表示了在三个坐标上的位移值。 glRotate*,把当前矩阵和一个表示旋转物体的矩阵相乘。物体将绕着(0,0,0)到(x,y,z)的直线以逆时针旋转,参数angle表示旋转的角度。 glScale*,把当前矩阵和一个表示缩放物体的矩阵相乘。x,y,z分别表示在该方向上的缩放比例。
注意我都是说“与XX相乘”,而不是直接说“这个函数就是旋转”或者“这个函数就是移动”,这是有原因的,马上就会讲到。
假设当前矩阵为单位矩阵,然后先乘以一个表示旋转的矩阵R,再乘以一个表示移动的矩阵T,最后得到的矩阵再乘上每一个顶点的坐标矩阵v。所以,经过变换得到的顶点坐标就是((RT)v)。由于矩阵乘法的结合率,((RT)v) = (R(Tv)),换句话说,实际上是先进行移动,然后进行旋转。即:实际变换的顺序与代码中写的顺序是相反的。由于“先移动后旋转”和“先旋转后移动”得到的结果很可能不同,初学的时候需要特别注意这一点。
OpenGL之所以这样设计,是为了得到更高的效率。但在绘制复杂的三维图形时,如果每次都去考虑如何把变换倒过来,也是很痛苦的事情。这里介绍另一种思路,可以让代码看起来更自然(写出的代码其实完全一样,只是考虑问题时用的方法不同了)。
让我们想象,坐标并不是固定不变的。旋转的时候,坐标系统随着物体旋转。移动的时候,坐标系统随着物体移动。如此一来,就不需要考虑代码的顺序反转的问题了。
以上都是针对改变物体的位置和方向来介绍的。如果要改变观察点的位置,除了配合使用glRotate*和glTranslate*函数以外,还可以使用这个函数:gluLookAt。它的参数比较多,前三个参数表示了观察点的位置,中间三个参数表示了观察目标的位置,最后三个参数代表从(0,0,0)到 (x,y,z)的直线,它表示了观察者认为的“上”方向。
2、投影变换
投影变换就是定义一个可视空间,可视空间以外的物体不会被绘制到屏幕上。(注意,从现在起,坐标可以不再是-1.0到1.0了!)
OpenGL支持两种类型的投影变换,即透视投影和正投影。投影也是使用矩阵来实现的。如果需要操作投影矩阵,需要以GL_PROJECTION为参数调用glMatrixMode函数。
glMatrixMode(GL_PROJECTION);
通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。
glLoadIdentity();
透视投影所产生的结果类似于照片,有近大远小的效果,比如在火车头内向前照一个铁轨的照片,两条铁轨似乎在远处相交了。
使用glFrustum函数可以将当前的可视空间设置为透视投影空间。其参数的意义如下图:

这个函数原型为:
void glFrustum(GLdouble left, GLdouble Right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far);
创建一个透视型的视景体。其操作是创建一个透视投影的矩阵,并且用这个矩阵乘以当前矩阵。这个函数的参数只定义近裁剪平面的左下角点和右上角点的三维空间坐标,即(left,bottom,-near)和(right,top,-near);最后一个参数far是远裁剪平面的离视点的距离值,其左下角点和右上角点空间坐标由函数根据透视投影原理自动生成。near和far表示离视点的远近,它们总为正值(near/far 必须>0)。
void mydisplay (void)
{
......
glMatrixMode (GL_PROJECTION);
LoadIdentity ();
Frustum (left, right, bottom, top, near, far);
......
}
2.gluPerspective():也可以使用更常用的gluPerspective函数

这个函数原型为:
void gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear, GLdouble zFar);
创建一个对称的透视型视景体,但它的参数定义于前面的不同,如图。其操作是创建一个对称的透视投影矩阵,并且用这个矩阵乘以当前矩阵。参数fovy定义视野在Y-Z平面的角度,范围是[0.0, 180.0];参数aspect是投影平面宽度与高度的比率;参数Near和Far分别是近远裁剪面到视点(沿Z负轴)的距离,它们总为正值。
以上两个函数缺省时,视点都在原点,视线沿Z轴指向负方向。
3.glOrtho():正投影相当于在无限远处观察得到的结果,它只是一种理想状态。但对于计算机来说,使用正投影有可能获得更好的运行速度。
使用glOrtho函数可以将当前的可视空间设置为正投影空间
这个函数的原型为:
glOrtho(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far)
六个参数, 前两个是x轴最小坐标和最大坐标,中间两个是y轴,最后两个是z轴值
它创建一个平行视景体(就是一个长方体空间区域)。
实际上这个函数的操作是创建一个正射投影矩阵,并且用这个矩阵乘以当前矩阵。
其中近裁剪平面是一个矩形,矩形左下角点三维空间坐标是(left,bottom,-near),
右上角点是(right,top,-near);远裁剪平面也是一个矩形,左下角点空间坐标是(left,bottom,-far),右上角点是(right,top,-far)。
注意,所有的near和far值同时为正或同时为负, 值不能相同。如果没有其他变换,正射投影的方向平行于Z轴,且视点朝向Z负轴。这意味着物体在视点前面时far和near都为负值,物体在视点后面时far和near都为正值。
只有在视景体里的物体才能显示出来。
如果最后两个值是(0,0),也就是near和far值相同了,视景体深度没有了,整个视景体都被压成个平面了,就会显示不正确。
gluLookAt 函数详解
void gluLookAt(GLdouble eyex,GLdouble eyey,GLdouble eyez,
#include <GL/glut.h> #include <stdlib.h> void init(void) { glClearColor (0.0, 0.0, 0.0, 0.0); //背景黑色 } void display(void) { glClear (GL_COLOR_BUFFER_BIT); glColor3f (1.0, 1.0, 1.0); //画笔白色 glLoadIdentity(); //加载单位矩阵 gluLookAt(0.0,0.0,5.0, 0.0,0.0,0.0, 0.0,1.0,0.0); glutWireTeapot(2); glutSwapBuffers(); } void reshape (int w, int h) { glViewport (0, 0, (GLsizei) w, (GLsizei) h); glMatrixMode (GL_PROJECTION); glLoadIdentity (); gluPerspective(60.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); gluLookAt (0.0, 0.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0); } int main(int argc, char** argv) { glutInit(&argc, argv); glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB); glutInitWindowSize (500, 500); glutInitWindowPosition (100, 100); glutCreateWindow (argv[0]); init (); glutDisplayFunc(display); glutReshapeFunc(reshape); glutMainLoop(); return 0; }
一、上面的display()函数中:gluLookAt(0.0,0.0,5.0, 0.0,0.0,0.0, 0.0,1.0,0.0); 相当于我们的脑袋位置在(0.0,0.0,5.0)处,眼睛望向(0.0,0.0,0.0),即原点。后面的三个参数(0.0,1.0,0.0),y轴为1,其余为0,表示脑袋朝上,就是正常的情况。看到的情况如下图:
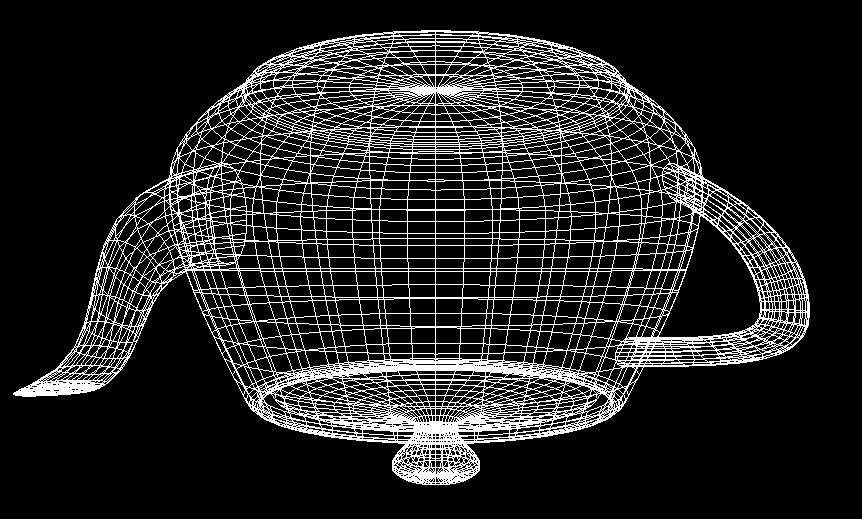
3、视口变换
当一切工作已经就绪,只需要把像素绘制到屏幕上了。这时候还剩最后一个问题:应该把像素绘制到窗口的哪个区域呢?通常情况下,默认是完整的填充整个窗口,但我们完全可以只填充一半。(即:把整个图象填充到一半的窗口内)
运用相机模拟方式,我们很容易理解视口变换就是类似于照片的放大与缩小。在计算机图形学中,它的定义是将经过几何变换、投影变换和裁剪变换后的物体显示于屏幕窗口内指定的区域内,这个区域通常为矩形,称为视口。
使用glViewport来定义视口。其中前两个参数定义了视口的左下脚(0,0表示最左下方),后两个参数分别是宽度和高度。
void glViewport(GLint x,GLint y,GLsizei width,GLsizei height);
在窗口中定义一个像素矩形,最终的图像将映射到这个矩形中。参数x和y指定了窗口内部视口的左下角,width和height指定了视口的大小。附:视口的纵横比一般和视景体的纵横比相同,若不同则当图像投影到视口时就会变形
4、操作矩阵堆栈
介于是入门教程,先简单介绍一下堆栈。你可以把堆栈想象成一叠盘子。开始的时候一个盘子也没有,你可以一个一个往上放,也可以一个一个取下来。每次取下的,都是最后一次被放上去的盘子。通常,在计算机实现堆栈时,堆栈的容量是有限的,如果盘子过多,就会出错。当然,如果没有盘子了,再要求取一个盘子,也会出错。
我们在进行矩阵操作时,有可能需要先保存某个矩阵,过一段时间再恢复它。当我们需要保存时,调用glPushMatrix函数,它相当于把矩阵(相当于盘子)放到堆栈上。当需要恢复最近一次的保存时,调用glPopMatrix函数,它相当于把矩阵从堆栈上取下。OpenGL规定堆栈的容量至少可以容纳32个矩阵,某些OpenGL实现中,堆栈的容量实际上超过了32个。因此不必过于担心矩阵的容量问题。
通常,用这种先保存后恢复的措施,比先变换再逆变换要更方便,更快速。
注意:模型视图矩阵和投影矩阵都有相应的堆栈。使用glMatrixMode来指定当前操作的究竟是模型视图矩阵还是投影矩阵。
5、综合举例
我们要制作的是一个三维场景,包括了太阳、地球和月亮。假定一年有12个月,每个月30天。每年,地球绕着太阳转一圈。每个月,月亮围着地球转一圈。即一年有360天。现在给出日期的编号(0~359),要求绘制出太阳、地球、月亮的相对位置示意图。(这是为了编程方便才这样设计的。如果需要制作更现实的情况,那也只是一些数值处理而已,与OpenGL关系不大)
首先,让我们认定这三个天体都是球形,且他们的运动轨迹处于同一水平面,建立以下坐标系:太阳的中心为原点,天体轨迹所在的平面表示了X轴与Y轴决定的平面,且每年第一天,地球在X轴正方向上,月亮在地球的正X轴方向。
下一步是确立可视空间。注意:太阳的半径要比太阳到地球的距离短得多。如果我们直接使用天文观测得到的长度比例,则当整个窗口表示地球轨道大小时,太阳的大小将被忽略。因此,我们只能成倍的放大几个天体的半径,以适应我们观察的需要。(百度一下,得到太阳、地球、月亮的大致半径分别是:696000km, 6378km,1738km。地球到太阳的距离约为1.5亿km=150000000km,月亮到地球的距离约为380000km。)
让我们假想一些数据,将三个天体的半径分别“修改”为:69600000(放大100倍),15945000(放大2500倍),4345000(放大5000倍)。将地球到月亮的距离“修改”为38000000(放大100倍)。地球到太阳的距离保持不变。
为了让地球和月亮在离我们很近时,我们仍然不需要变换观察点和观察方向就可以观察它们,我们把观察点放在这个位置:(0, -200000000, 0) ——因为地球轨道半径为150000000,咱们就凑个整,取-200000000就可以了。观察目标设置为原点(即太阳中心),选择Z轴正方向作为 “上”方。当然我们还可以把观察点往“上”方移动一些,得到(0, -200000000, 200000000),这样可以得到45度角的俯视效果。
为了得到透视效果,我们使用gluPerspective来设置可视空间。假定可视角为60度(如果调试时发现该角度不合适,可修改之。我在最后选择的数值是75。),高宽比为1.0。最近可视距离为1.0,最远可视距离为200000000*2=400000000。即:gluPerspective (60, 1, 1, 400000000);
现在我们来看看如何绘制这三个天体。
为了简单起见,我们把三个天体都想象成规则的球体。而我们所使用的glut实用工具中,正好就有一个绘制球体的现成函数:glutSolidSphere,这个函数在“原点”绘制出一个球体。由于坐标是可以通过glTranslate*和glRotate*两个函数进行随意变换的,所以我们就可以在任意位置绘制球体了。函数有三个参数:第一个参数表示球体的半径,后两个参数代表了“面”的数目,简单点说就是球体的精确程度,数值越大越精确,当然代价就是速度越缓慢。这里我们只是简单的设置后两个参数为20。
太阳在坐标原点,所以不需要经过任何变换,直接绘制就可以了。
地球则要复杂一点,需要变换坐标。由于今年已经经过的天数已知为day,则地球转过的角度为day/一年的天数*360度。前面已经假定每年都是360天,因此地球转过的角度恰好为day。所以可以通过下面的代码来解决:
glRotatef(day, 0, 0, -1);
/* 注意地球公转是“自西向东”的,因此是饶着Z轴负方向进行逆时针旋转 */ glTranslatef(地球轨道半径, 0, 0); glutSolidSphere(地球半径, 20, 20);
月亮是最复杂的。因为它不仅要绕地球转,还要随着地球绕太阳转。但如果我们选择地球作为参考,则月亮进行的运动就是一个简单的圆周运动了。如果我们先绘制地球,再绘制月亮,则只需要进行与地球类似的变换:
glRotatef(月亮旋转的角度, 0, 0, -1); glTranslatef(月亮轨道半径, 0, 0); glutSolidSphere(月亮半径, 20, 20);
但这个“月亮旋转的角度”,并不能简单的理解为day/一个月的天数30*360度。因为我们在绘制地球时,这个坐标已经是旋转过的。现在的旋转是在以前的基础上进行旋转,因此还需要处理这个“差值”。我们可以写成:day/30*360 - day,即减去原来已经转过的角度。这只是一种简单的处理,当然也可以在绘制地球前用glPushMatrix保存矩阵,绘制地球后用glPopMatrix恢复矩阵。再设计一个跟地球位置无关的月亮位置公式,来绘制月亮。通常后一种方法比前一种要好,因为浮点的运算是不精确的,即是说我们计算地球本身的位置就是不精确的。拿这个不精确的数去计算月亮的位置,会导致 “不精确”的成分累积,过多的“不精确”会造成错误。我们这个小程序没有去考虑这个,但并不是说这个问题不重要。
还有一个需要注意的细节: OpenGL把三维坐标中的物体绘制到二维屏幕,绘制的顺序是按照代码的顺序来进行的。因此后绘制的物体会遮住先绘制的物体,即使后绘制的物体在先绘制的物体的“后面”也是如此。使用深度测试可以解决这一问题。使用的方法是:1、以GL_DEPTH_TEST为参数调用glEnable函数,启动深度测试。2、在必要时(通常是每次绘制画面开始时),清空深度缓冲,即:glClear(GL_DEPTH_BUFFER_BIT);其中,glClear (GL_COLOR_BUFFER_BIT)与glClear(GL_DEPTH_BUFFER_BIT)可以合并写为:
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
且后者的运行速度可能比前者快。
到此为止,我们终于可以得到整个“太阳,地球和月亮”系统的完整代码。
Code:
// 太阳、地球和月亮 // 假设每个月都是30天 // 一年12个月,共是360天 static int day = 200; // day的变化:从0到359 void myDisplay(void) { glEnable(GL_DEPTH_TEST); glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(75, 1, 1, 400000000); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); gluLookAt(0, -200000000, 200000000, 0, 0, 0, 0, 0, 1); // 绘制红色的“太阳” glColor3f(1.0f, 0.0f, 0.0f); glutSolidSphere(69600000, 20, 20); // 绘制蓝色的“地球” glColor3f(0.0f, 0.0f, 1.0f); glRotatef(day/360.0*360.0, 0.0f, 0.0f, -1.0f); glTranslatef(150000000, 0.0f, 0.0f); glutSolidSphere(15945000, 20, 20); // 绘制黄色的“月亮” glColor3f(1.0f, 1.0f, 0.0f); glRotatef(day/30.0*360.0 - day/360.0*360.0, 0.0f, 0.0f, -1.0f); glTranslatef(38000000, 0.0f, 0.0f); glutSolidSphere(4345000, 20, 20); glFlush(); }
试修改day的值,看看画面有何变化。
小结:本课开始,我们正式进入了三维的OpenGL世界。
OpenGL通过矩阵变换来把三维物体转变为二维图象,进而在屏幕上显示出来。为了指定当前操作的是何种矩阵,我们使用了函数glMatrixMode。
我们可以移动、旋转观察点或者移动、旋转物体,使用的函数是glTranslate*和glRotate*。
我们可以缩放物体,使用的函数是glScale*。
我们可以定义可视空间,这个空间可以是“正投影”的(使用glOrtho或gluOrtho2D),也可以是“透视投影”的(使用glFrustum或gluPerspective)。
我们可以定义绘制到窗口的范围,使用的函数是glViewport。
矩阵有自己的“堆栈”,方便进行保存和恢复。这在绘制复杂图形时很有帮助。使用的函数是glPushMatrix和glPopMatrix。
好了,艰苦的一课终于完毕。我知道,本课的内容十分枯燥,就连最后的例子也是。但我也没有更好的办法了,希望大家能坚持过去。不必担心,熟悉本课内容后,以后的一段时间内,都会是比较轻松愉快的了。



