求极限的方法总结

求极限的方法总结

两个重要极限：

\(\Large \underset{x\rightarrow 0}{\lim}\frac{\sin x}{x} = 1\)

\(\Large \underset{x\rightarrow \infty}{\lim}(1+\frac{1}{x})^x=e\)

1. 直接代入

函数在某点连续，函数在该点的极限等于该点的函数值
一切初等函数在其定义区间内都是连续的，都可以用直接代入法

2. 夹逼准则

3. 等价替换

把某个表达式替换为和它等价的表达式

常用替换：

当x趋近于0时，有：

\(\sin x \sim x，\tan x \sim x，\arcsin x \sim x，\arctan x \sim x\)

\(1-\cos x \sim {\Large \frac{x^2}{2}} ， a^x-1 \sim xlna ，e^x-1 \sim x\)

\(ln(1+x) \sim x ，(1+x)^a-1 \sim ax\)

4. 洛必达法则

不是未定式 \(\frac{0}{0} 或 \frac{\infty}{\infty}\) 不能用洛必达法则

5. 单调有界定理

单调且有界的数列必有极限，对于函数也一样，单调且有界的趋近过程也必有极限。

6. 无穷小乘以有界量等于无穷小

定理1: 两个无穷小的和是无穷小。
  有限个无穷小之和也是无穷小

定理2: 有界函数与无穷小的乘积是无穷小.
  推论1: 常数与无穷小的乘积是无穷小.
  推论2: 有限个无穷小的乘积是无穷小.

例5：求极限 \(\underset{x\rightarrow \infty}{\lim}\frac{1}{x}\sin 3x\)

解析：当x趋近于无穷时，1/x为无穷小，sin3x为有界量（不大于1），因此该极限为0。

7. 大头法则

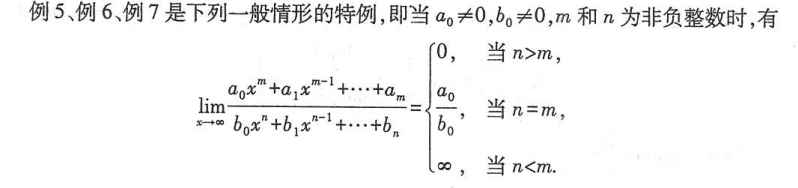
8. 取倒数

第四节：