Part 1:代码分析
- 前言
对于OO第一单元的学习,我个人深刻体会到了面向对象设计中,层次化设计的重要性。首先需要明白自己的代码将如何构成,将基本的框架搭建好,其次才是具体的实现。然而第一次作业时我对整体程序的架构思考并不够深入,为简化工作快速完成实验作业决定以预解析处理的方式读入数据。在之后遇到第二三次作业的同时又正好需要花费大量精力参与课外竞赛,没有额外重构代码的时间,导致不得不选择继续在第一次作业的基础上进行迭代开发,最终三次作业都以预处理的形式完成,痛失大量得分。
之后本文将着重于预解析处理模式下我个人的思考与解决方案,谈谈OO第一单元的学习后我所得到的收获。
- 思路
可以看出,预解析后的表达式实际上是一棵二叉表达式树,故我们可以将工作分为两部分:
第一部分是处理表达式树,在这个过程中去除可以删除的括号,将加减运算送往树的顶端,同时将乘和幂运算送向树的叶节点,经过若干次这样的操作,我们将得到一个在根节点附近以加法和负数运算为主、在叶节点附近以乘法、幂运算和三角函数为主的一棵表达式树。针对第三次作业,可以对三角函数中的内容构建一棵新树,使之结构与前面的描述一致,这样就能够递归下降,直到整棵表达式树及其子树都无法再拆解括号化简。
具体需要化简的计算:(假设该计算不位于叶节点)
1.对add计算,不进行处理;
2.对sub计算,修改为a +(- b);
3.对pos计算,直接用其子运算进行替代;
4.对neg计算,将其子运算取负数;
5.对mul计算,进行类似(a+b)*(c+d)= ac + ad + bc + bd 的化简运算;
6.对pow计算,修改为若干个子运算的乘积;
7.对sin、cos计算,以其子运算为根节点,调用以上过程的处理函数递归化简。
第二部分是输出表达式树,在这一步骤中主要是进行输出数据结构的构建与同类项的合并。对于输出的数据结构(称之为Polynomial)可以概括为多个不可加的unit的和,每个unit的构成如下:
axb∏sin i(ƒ(x))∏cos j(ƒ(x))
其中,f(x)、i、j 的内容为任意符合要求的式子与值
1.可以用系数 a、指数 b、三角函数集∏sin i(ƒ(x))∏cos j(ƒ(x)) 来描述一个unit(对于数字,可使得指数为0,函数集为空;对于x或-x,可使得系数为1或-1,指数为1,函数集为 空);
2.三角函数集中每个三角函数可以用用类型(sin值为1,cos值为2)、指数 i (j)、内容函数ƒ(x) 来描述,其内容函数又是若干个unit的和(即内容函数为Polynomial)。
运算时在二叉树的每一个节点访问其左右子节点,调用运算方法生成左右子节点各自的Polynomial,再对这两个Polynomial进行同类项的合并。合并时进入双循环,判断两个Unit之间是否具有可加性,如果两个unit指数相同、三角函数集内的函数两两相同则判断为可加,进行合并。对整个经过第一部分处理的二叉树遍历后,就能得到一个最简的unit集合(也就是Polynomial),将该集合输出即是最终符合要求的表达式。
- 代码量度
以第三次作业最终版本为例:
| Source File | Total Lines | Source Code Lines | Source Code Lines[%] | Comment Lines | Comment Lines[%] | Blank Lines | Blank Lines[%] |
| CalStep.java | 457 | 425 | 0.9299781181619255 | 10 | 0.02188183807439825 | 22 | 0.04814004376367615 |
| Expression.java | 119 | 100 | 0.8403361344537815 | 6 | 0.05042016806722689 | 13 | 0.1092436974789916 |
| Main.java | 35 | 24 | 0.6857142857142857 | 6 | 0.17142857142857143 | 5 | 0.14285714285714285 |
| Polynomials.java | 436 | 411 | 0.9426605504587156 | 5 | 0.011467889908256881 | 20 | 0.045871559633027525 |
| Processor.java | 65 | 61 | 0.9384615384615385 | 0 | 0.0 | 4 | 0.06153846153846154 |
| TriFunc.java | 58 | 52 | 0.896551724137931 | 0 | 0.0 | 6 | 0.10344827586206896 |
| Unit.java | 205 | 192 | 0.9365853658536586 | 0 | 0.0 | 13 | 0.06341463414634146 |
- UML图
以第三次作业最终版本为例:

类功能分析
1.Main:调用各个类以输出最终结果;
2.Expression:将输入的计算步骤以LinkedList形式存储。其中,重点方法包含处理表达式树的方法、向LinkedList中增加计算步骤的方法和判断处理是否完成的方法;
3.CalStep:存储每一个计算步骤,并对每一个计算步骤不同的计算操作作出相应的处理;
4.Processor:存储完成第一步去括号处理后的表达式树。包含合并同类项的方法,该方法输出一个符合要求的Polynomial;
5.Polynomials:存放若干个Unit,可以进行Polynomial间的合并同类项操作且可以输出Polynomial对应的字符串;
6.Unit:以思路中的形式存放每个项,可以进行Unit间的比较与合并操作,也能够输出Unit对应的字符串;
7.TriFunc:以思路中的形式存放单个三角函数。可以比较三角函数、合并三角函数,也能够输出三角函数对应的字符串。
优点
类图很好的反映了程序的架构。程序主要由两部分构成,其一:预处理解析式的二叉树分析(Expression);其二:二叉树合并并翻译为表达式字符串输出(Processor)。而为了完成前者的任务,引入类CalStep进行表达式二叉树的化简运算,为了完成后者任务,设计了一个数据结构Polynomials及其子结构Unit与TriFunc(可递归调用)来进行表达式的合并与存储,最后可以使用方法StringOut递归输出表达式字符串。可见类的数量相对较少,每一个类的职责明确,架构上从高到低层层递进,逻辑较为清晰。
缺点
可以看出,部分类的行数很长且内容冗杂,具体其实是类的方法设计上存在漏洞。首先,一些用于文法分析的方法被分散地装进了几个类中,而在需要夸类调用解析方法时就会较为繁琐,缺少逻辑性;其次,如CalStep类、Polynomials类、Unit类等都含有与运算相关的方法,这些运算具有一定的相似性,但还是被分装在了不同的类当中,导致观感上非常繁琐;最后,构建的表达式数据结构主要用以输出,而在原本的类关系中没有具体体现出输出的思想。
因此经过相应优化后,新的类图如下(接口部分的线条显示有误,使用的是Interface Realization):
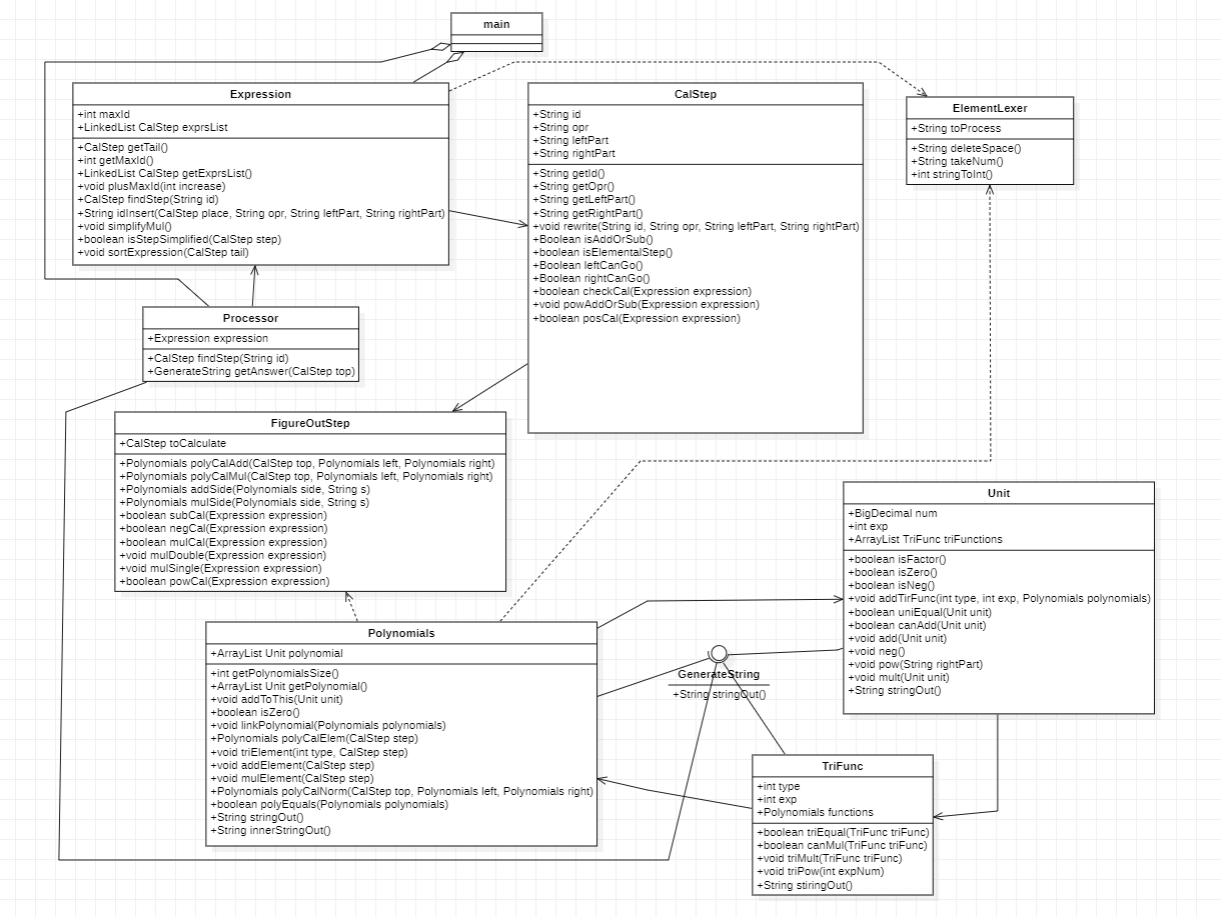
Part 2:Bug分析
- 自身bug分析
第一次作业:由于第一次作业未对复杂性进行控制,导致程序逻辑冗杂,在递归分析计算表达式二叉树时分支错误地走到了空指针上引发bug。具体错误位置在类CalStep的mulCal方法中,进行boolean运算的Calstep对象有可能指向空指针。修改方法为:给boolean表达式增加条件,如:CalStep对象!=null && 原表达式 即可解决该bug。
第二次作业:第二次作业输出错误,原因在于对sum运算(即连续的add)的处理上有逻辑漏洞,会跳过其中的某几步。具体错误位置在类 Polynomials的polyCalAdd方法中,多个Polynomials对象的相加时会跳过需要相加的部分。修改方法:由于bug较为复杂,因此新构造了一个方法simplifySum来先把sum的多个Polynomials合成单个polynomials,再进入方法中进行计算。
第三次作业:本次作业出现了两个bug,其一为字符串输出时会被错误的删除符号;其二为在进行较多mul运算时会出现死循环。前者位于Polynomials的stringOut方法,遇到负数时项前方的运算符号和项的负号会被额外删除;后者位于Expression的sortExpression方法,在sortExpression连续遇到mul时会进行错误的运算进入死循环。修改方法:对第一个错误进行了表达式输出逻辑的优化,不仅减短输出长度,而且使得负号输出正确;对第二个错误则在Expression中新增方法simplufyMul,先进行部分乘法运算的处理,以让sortExpression中的判断与运算逻辑能够正确运行。
经过比较,出现了bug的方法和未出现bug的方法间,出bug处的方法长度往往较长、判断语句相对复杂、计算处理相对冗杂。
- hack时策略
由于个人时间原因以及对于互测模式缺乏兴趣,在第一单元几次作业的互测中,我个人仅仅简单地参与了一下。对于互测时的策略,可以考虑测试边界条件、测试稍大的幂运算、测试连续的正负号等方法。需要根据作业的类型来具体确定。
Part 3:设计体验
第一单元的学习对我而言还是较为困难的,首先缺乏对java语言掌握和运用的熟练度,其次在面向对象设计的思想上也非常的生涩,再加上开学时需要集中处理课外活动与展示课程的竞赛,对于第一单元的学习我自认为是不够到位的。不过经过三次作业的练习,还是基本掌握了一单元着重强调的层次化设计的思想。层次化设计让复杂的内容得以分割成小块,再对每一个小块继续分割处理,经过多次的递归后我们所需要处理的内容仅剩最基本的单元。这种化繁为简、深入浅出的架构模式具有很大的优势,不仅遇到新需求时便于迭代,而且便于后来者阅读和理解,逻辑性十分强。
在今后的课程中,我也将尝试将这样的设计架构理念内化为个人所熟练掌握的基本方法,以应对未来的更多挑战。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号