浅谈压缩感知（十九）：MP、OMP与施密特正交化

关于MP、OMP的相关算法与收敛证明，可以参考：http://www.cnblogs.com/AndyJee/p/5047174.html，这里仅简单陈述算法流程及二者的不同之处。

主要内容：

MP的算法流程及其MATLAB实现
OMP的算法流程以及MATLAB实现
MP与OMP的区别
施密特正交化与OMP的关系

一、MP（匹配追踪）的算法流程：

二、MP的MATLAB实现：

% MP：匹配追踪算法
% dictionary: 超完备字典
% x: 待表示信号
% M = 4; N = 10;
% Phi = randn(M,N); % 字典
% for nn = 1:N
%     Phi(:,nn) = Phi(:,nn)/norm(Phi(:,nn));
% end
% b = randn(M,1); % 信号
function x = MP(dictionary,x,iter)
[M,N] = size(dictionary);
residual = zeros(M,iter); %残差矩阵，保存每次迭代后的残差
residual(:,1) = x; %初始化残差为x
L = size(residual,2); %得到残差矩阵的列
pos_num = zeros(1,L); %用来保存每次选择的列序号
resi_norm = zeros(1,L); %用来保存每次迭代后的残差的2范数
resi_norm(1) = norm(x); %因为前面已初始化残差为x
iter_out = 1e-3;
iter_count = 0;

for mm = 1:iter
    %迭代退出条件
    if resi_norm(mm) < iter_out
        break;
    end
    %求出dictionary每列与上次残差的内积
    scalarproducts = dictionary'*residual(:,mm);
     %找到内积中最大的列及其内积值
    [val,pos] = max(abs(scalarproducts));
    %更新残差
    residual(:,mm+1) = residual(:,mm) - scalarproducts(pos)*dictionary(:,pos);
    %计算残差的2范数（平方和再开根号）
    resi_norm(mm+1) = norm(residual(:,mm+1));
     %保存选择的列序号
    pos_num(mm) = pos;
    iter_count = iter_count + 1;
end
%绘出残差的2范数曲线
resi_norm = resi_norm(1:iter_count+1);
plot(resi_norm);grid;
%显示选择的字典原子
pos_num = pos_num(1:iter_count);
disp(pos_num);
%稀疏系数(稀疏表示)
dict = dictionary(:,pos_num);
y_vec = (dict'*dict)^(-1)*dict'*x;
disp(y_vec);
figure;plot(y_vec);

三、OMP（正交匹配追踪）的算法流程：

四、OMP的MATLAB实现：

% MP：匹配追踪算法
% dictionary: 超完备字典
% x: 待表示信号
% M = 4; N = 10;
% Phi = randn(M,N); % 字典
% for nn = 1:N
%     Phi(:,nn) = Phi(:,nn)/norm(Phi(:,nn));
% end
% b = randn(M,1); % 信号
function x = OMP(dictionary,x,iter)
[M,N] = size(dictionary);
residual = zeros(M,iter); %残差矩阵，保存每次迭代后的残差
residual(:,1) = x; %初始化残差为x
L = size(residual,2); %得到残差矩阵的列
pos_num = zeros(1,L); %用来保存每次选择的列序号
resi_norm = zeros(1,L); %用来保存每次迭代后的残差的2范数
resi_norm(1) = norm(x); %因为前面已初始化残差为x
iter_out = 1e-3;
iter_count = 0;
aug_mat = [];

for mm = 1:iter
    %迭代退出条件
    if resi_norm(mm) < iter_out
        break;
    end
    %求出dictionary每列与上次残差的内积
    scalarproducts = dictionary'*residual(:,mm);
    %找到内积中最大的列及其内积值
    [val,pos] = max(abs(scalarproducts));
    %最小二乘的增广矩阵
    aug_mat = [aug_mat dictionary(:,pos)];
    %最小二乘投影
    proj_y = aug_mat*(aug_mat'*aug_mat)^(-1)*aug_mat'*x;
    %更新残差
    residual(:,mm+1) = x - proj_y;
    %计算残差的2范数（平方和再开根号）
    resi_norm(mm+1) = norm(residual(:,mm+1));
     %保存选择的列序号
    pos_num(mm) = pos;
    iter_count = iter_count + 1;
end
%绘出残差的2范数曲线
resi_norm = resi_norm(1:iter_count+1);
plot(resi_norm);grid;
%显示选择的字典原子
pos_num = pos_num(1:iter_count);
disp(pos_num);
%稀疏系数
dict = dictionary(:,pos_num);
y_vec = (dict'*dict)^(-1)*dict'*x;
disp(y_vec);
figure;plot(y_vec);

五、MP与OMP的区别：

OMP与MP的不同根本在于残差更新过程：OMP减去的Pe_m是e_m在所有被选择过的原子组成的矩阵Φ_t所张成空间上的正交投影，而MP减去的Pe_m是e_m在本次被选择的原子φ_m所张成空间上的正交投影。基于此，OMP可以保证已经选择过的原子不会再被选择。

六、施密特（Schimidt）正交化与OMP

1、施密特(Schimidt)正交化的过程:

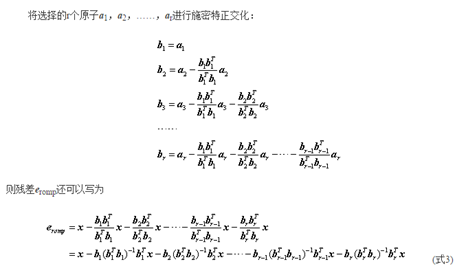
上面的的[x,y]表示向量内积，[x,y]=x^Ty=y^Tx=[x,y]。施密特正交化公式中的b_r实际上可写为：

分子之所以可以这么变化是由于[x,y]实际上为一个数，因此[x,y]x=x[x,y]= xx^Ty。

2、OMP与施密特(Schimidt)正交化的关系：

结论：OMP分解过程，实际上是将所选原子依次进行Schimidt正交化，然后将待分解信号减去在正交化后的原子上各自的分量即可得残差。其实(式3)求残差的过程也是在进行施密特正交化。

3、验证OMP残差求解过程与Schmidt正交化的关系

% 验证OMP残差求解过程与Schmidt正交化的关系
%
clc;clear;close all;
M = 4; N = 10;
Phi = randn(M,N); % 字典
for nn = 1:N
    Phi(:,nn) = Phi(:,nn)/norm(Phi(:,nn));
end
b = randn(M,1); % 信号
res0 = b; % 初始化残差为待稀疏信号b
% OMP
% 选择字典第一个原子
c1 = Phi'* res0; % 求矩阵Phi各列与b的内积
[val1,pos1] = max(abs(c1)); % 找到内积中最大的列及其内积值
phit = [Phi(:,pos1)]; % 由所有选出的列组合的矩阵
Pphi = phit*(phit'*phit)^(-1)*phit'; % 正交投影变换矩阵
omp_res1 = res0 - Pphi*res0; % OMP用上一次残差减去残差在phit列空间的正交投影
omp_resb = b - Pphi*b; % OMP用待稀疏信号b减去b在phit列空间的正交投影
% Schimidt
x = Phi(:,pos1); % Schimidt正交化第一个向量
Px = x*(x'*x)^(-1)*x';
smt_res1 = res0 - Px*b; % 实际上是b - Px*b
% test 
norm(omp_res1-omp_resb)
norm(omp_resb-smt_res1)

% OMP
% 选择字典第二列
c2 = Phi' * omp_res1;
[val2,pos2] = max(abs(c2));
phit = [Phi(:,pos1) Phi(:,pos2)]; 
Pphi = phit*(phit'*phit)^(-1)*phit';
omp_res2 = omp_res1 - Pphi*omp_res1;
omp_resb = b - Pphi*b;
% Schimidt
y = Phi(:,pos2) - Px*Phi(:,pos2); % Schimidt正交化第二个向量
Py = y*(y'*y)^(-1)*y';
smt_res2 = smt_res1 - Py*b; % 实际上是b - Px*b - Py*b，上一次残差减去b在第2列正交化所得z上的投影
% test
norm(omp_res2-omp_resb)
norm(omp_resb-smt_res2)

% OMP
% 选择字典第三列
c3 = Phi' * omp_res2;
[val3,pos3] = max(abs(c3));
phit = [Phi(:,pos1) Phi(:,pos2) Phi(:,pos3)];
Pphi = phit*(phit'*phit)^(-1)*phit';
omp_res3 = omp_res2 - Pphi*omp_res2; 
omp_resb = b - Pphi*b;
% Schimidt
z = Phi(:,pos3) - Px*Phi(:,pos3) - Py*Phi(:,pos3);  % Schimidt正交化第三个向量
Pz = z*(z'*z)^(-1)*z';
smt_res3 = smt_res2 - Pz*b; % 实际上是b - Px*b - Py*b - Pz*b，上一次残差减去b在第3列正交化所得z上的投影
% test
norm(omp_res3-omp_resb)
norm(omp_resb-smt_res3)