浅谈压缩感知(十五):感知矩阵之spark常数
在压缩感知中,有一些用来评价感知矩阵(非测量矩阵)的指标,如常见的RIP等,除了RIP之外,spark常数也能够用来衡量能否成为合适的感知矩阵。
0、相关概念与符号

1、零空间条件NULL Space Condition
在介绍spark之前,先考虑一下感知矩阵的零空间。
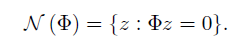
这里从矩阵的零空间来考虑测量矩阵需满足的条件:对于K稀疏的信号x,当且仅当测量矩阵的零空间与2K个基向量张成的线性空间没有交集,或者说零空间中的向量不在2K个基向量张成的线性空间中。
上述描述的性质似乎有点难懂,那么与之等价的表述就是spark常数。

2、spark常数定义
简单来说就是,矩阵列线性相关向量组的最小数目。(注意,这里的矩阵指的是感知矩阵,即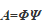 ,并非测量矩阵或稀疏基)
,并非测量矩阵或稀疏基)
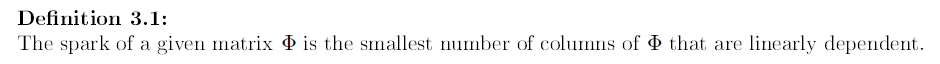
3、spark评价定理
当且仅当spark(Φ)>2k时,可以通过最小0范数优化问题得到k-稀疏信号x的精确近似。
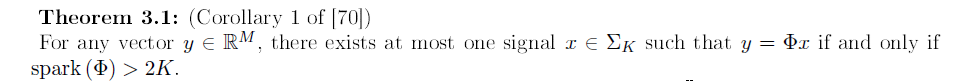
4、线性相关
定义:

定理:

性质:

5、定理证明
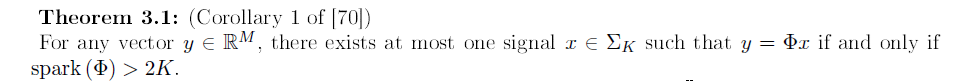
反证法。
第一步证明:对于任意的向量y,存在至多一个K稀疏的信号x,使得 ,则
,则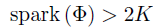 。
。
证明:假设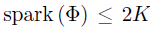 ,即根据定义感知矩阵的线性相关列小于或等于2K,从线性相关的定义出发,
,即根据定义感知矩阵的线性相关列小于或等于2K,从线性相关的定义出发,
存在某个向量 ,即
,即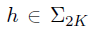 ,使得
,使得 且h不等于0。
且h不等于0。
由于 ,则h可以表示为:
,则h可以表示为: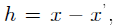
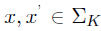 ,因此
,因此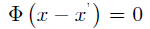
从而得到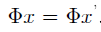 。
。
但是我们的条件中说明了至多只有一个K稀疏的信号x,因此与原条件矛盾,故假设不成立,原命题成立。
第二步证明:对于任意的向量y,满足 且
且 的K稀疏信号x至多有一个。
的K稀疏信号x至多有一个。
证明:假设K稀疏信号x至少有两个,设为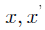 ,则
,则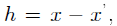
 。
。
因为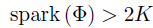 ,即根据定义感知矩阵的线性相关列大于2K,从线性相关的定义出发,
,即根据定义感知矩阵的线性相关列大于2K,从线性相关的定义出发,
存在某个向量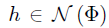 ,使得
,使得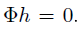 ,且h不等于0。而感知矩阵的零空间应该大于2K维,而假设中的h所在子空间小于或等于2K维,要满足
,且h不等于0。而感知矩阵的零空间应该大于2K维,而假设中的h所在子空间小于或等于2K维,要满足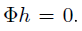 ,当且仅当h=0的时候,即
,当且仅当h=0的时候,即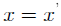 ,与原假设矛盾,因此假设不成立,原命题成立。
,与原假设矛盾,因此假设不成立,原命题成立。
6、spark常数与矩阵的秩
虽然spark与秩(rank)在某些方面很相似,但它们实际上是完全不同的,矩阵的秩是最大的线性无关的列数,而Spark是最小的线性相关的列数;有的时候矩阵满秩但spark=2。
还是通过例子理解吧:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号