浅谈压缩感知（十）：范数与稀疏性

问题：

压缩感知中算法会通过L0，L1范数建立的数学模型得到一个稀疏解，那么为什么L0，L1范数会导致一个稀疏解呢？

分析与解释：

1、范数

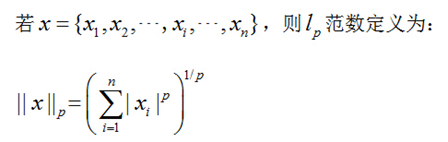
常见的有L0范数、L1范数、L2范数，经常要将L0范数等价为L1范数去求解，因为L1范数求解是一个凸优化问题，而L0范数求解是一个NP难问题。

（关于NP问题：参考阅读http://www.cnblogs.com/AndyJee/p/5048556.html）

L0范数指的是x中非零元素的个数，即x的稀疏度，如果x是K稀疏的，则L0范数等于K；

L1范数指的是x中所有元素模值的和；

L2范数指的是x中所有元素模值平方的和再开方，它代表着距离的概念；

还有无穷范数，指的是x中元素模的最大值。

2、稀疏性

在压缩感知里经常提到 "K稀疏" 的概念，这个是很容易理解的：也就是对于长度为N的向量（实际上是指一个N维离散离值信号）来说，它的N个元素值只有K个是非零的，其中K<<N，这时我们称这个向量是K稀疏的或者说是严格K稀疏的；实际中要做到严格K稀疏不容易，一般来说，只要除了这K个值其它的值很小很小，我们就认为向量是稀疏的，这时区别于严格K稀疏且就叫它K稀疏吧。

为什么要谈稀疏这个问题呢？因为如果信号是稀疏的，则它是可压缩的，也就是说里面那么多零，我只记录那些非零值及它的位置就好了。

当然，现实中的信号本身一般并不是稀疏的，但经过一个变换后，在一组基上面是稀疏的，这就是信号的稀疏表示。

稀疏性是压缩感知的前提。

3、范数与稀疏性

压缩感知的数学模型表示：

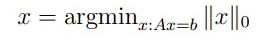
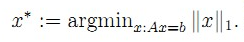
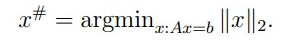
数学模型求解的几何表示：

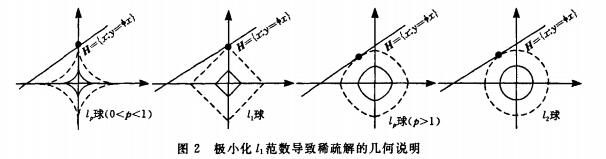
AX=b：表示空间中的一条直线；

||X||p：表示空间中的Lp球；

当0<p<1时，Lp球是内凸的，当球的半径逐渐增加时与直线的交点将位于坐标轴上，而坐标轴上的点是稀疏的（除了该所在坐标轴的坐标值不为0外，其他均为0）；

当p=1时，Lp球是菱状，在一定条件下会导致一个稀疏解，即相交于坐标轴上；（这也许是压缩感知中L0模型在一定条件下等价于L1模型的形象解释吧）

当p>1时，Lp球是外凸的，当逐渐膨胀时与直线的切点一定不位于坐标轴上，即此时的解是不稀疏的。如图中的L2球。