HAOI2010 软件安装

题目链接

Solution

如果 \(\mathrm{A}\) 的安装依赖于 \(\mathrm{B}\)，那么从 \(\mathrm{B}\) 到 \(\mathrm{A}\) 连一条有向边。

观察到题面中的一句话：一个软件最多依赖另外一个软件。也就是说，每个点的入度最多为 \(1\). 仔细思考可以发现，这些物品之间构成的图只存在树状结构和简单环。

为了处理掉这些环，我们可以缩点，把缩点后每个点的重量计为原物品的重量之和，价值计为原物品的价值之和。为防止图不连通，把 \(n+1\) 号点连向所有入度为 \(0\)的点，这样一来，这张图就彻彻底底的变成了一棵树。

剩下的部分跟 CTSC1997 选课 很像，就是一个树形 \(\mathrm{dp}\) 了。

可以简单的画一张图看一下：

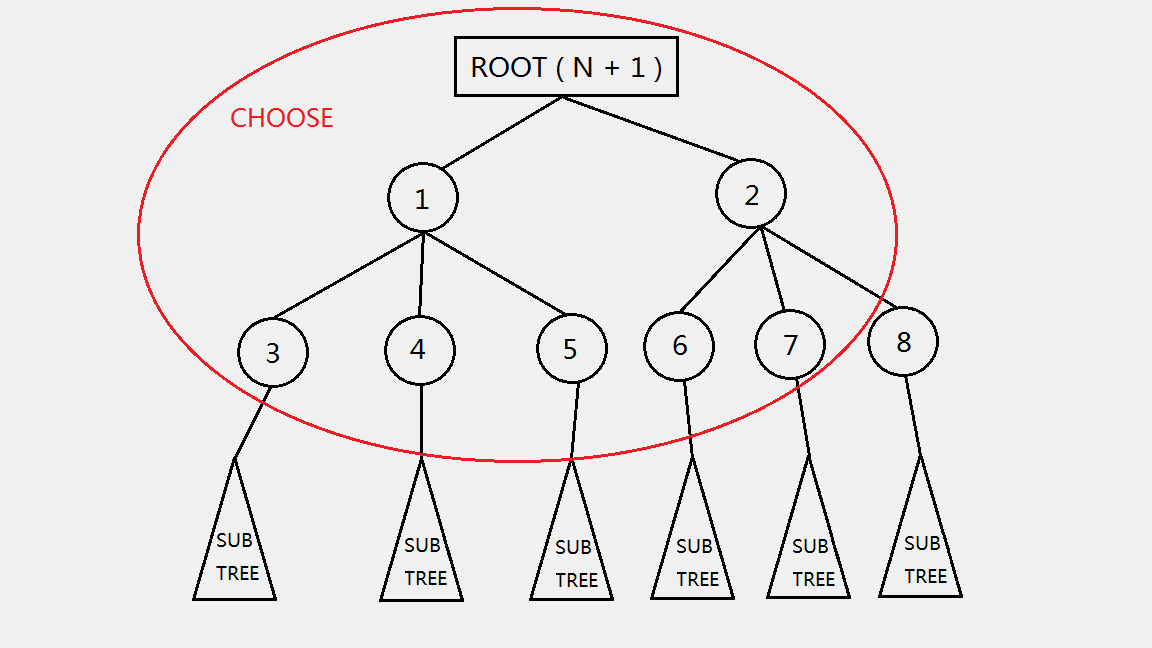
红圈圈出的点就是一个合法的选择方案（设 \(\mathrm{root}\) 节点的重量和体积都是 \(0\)，并强制选择该节点）

结合上文，发现选择每个点之前，其祖先节点也一定被选择。更形象地说，一个合法的选取方案是一个包括根在内的联通块。

这样我们就可以设出状态：\(f_{i,j}\) 表示以节点 \(i\) 为根的子树，选择了节点 \(i\)，占用体积为 \(j\) 的最大价值。对于 \(i\) 的每个子树，枚举其占据的体积 \(k \space (0 \leq k \leq j-wei_i)\)，进行 \(01\) 背包。转移方程式：

\[f_{i,j+wei_i}= \max \left\{ f_{v,k}+f_{x,j+wei_i-k} \}\right. \space (j \in [0,M-wei_i], \space k \in [0,j], \space v \in \left\{ son_i \}\right.) \]

缩点一定要注意各种细节，稍一不注意就可能会变成 \(\mathrm{40pts}\)、\(\mathrm{10pts}\) 甚至 \(0pts\).

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;

const int N = 2333;

//input---------------------
LL n, m;
LL wei[N], val[N], d[N], W[N], V[N], rd[N];

//edge----------------------
struct edge { LL nxt, to; } e[N];
LL cnt = 0, head[N];

//tarjan--------------------
LL id = 0, top = 0, color = 0;
LL dfn[N], vis[N], low[N], st[N], col[N];

//dp--------------------------
LL f[N][N], g[N][N];

void tarjan(LL x)
{
    st[++top] = x;
    vis[x] = 1;
    low[x] = dfn[x] = ++id;
    for(int i = head[x]; i; i = e[i].nxt)
    {
        LL v = e[i].to;
        if(!dfn[v]) tarjan(v), low[x] = min(low[x], low[v]);
        else if(vis[v]) low[x] = min(low[x], dfn[v]);
    }
    if(low[x] == dfn[x])
    {
        color++;
        st[top + 1] = -1;
        while(st[top + 1] != x)
        {
            col[st[top]] = color;
            vis[st[top--]] = 0;
        }
    }
}

void add(LL x, LL y)
{
    e[++cnt] = (edge) { head[x], y };
    head[x] = cnt;
}

void Clear()
{
    memset(f, 0, sizeof(f));
    memset(rd, 0, sizeof(rd));
    memset(wei, 0, sizeof(wei));
    memset(val, 0, sizeof(val));
    memset(col, 0, sizeof(col));
    memset(vis, 0, sizeof(vis));
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(head, 0, sizeof(head));
}

void dfs(LL x)
{
    for(int i = wei[x]; i <= m; i++) f[x][i] = val[x];
    for(int i = head[x]; i; i = e[i].nxt)
    {
        LL v = e[i].to;
        dfs(v);
        for(int j = m - wei[x]; j >= 0; j--)
            for(int k = 0; k <= j; k++)
                f[x][j + wei[x]] = max(f[x][j + wei[x]], f[v][k] + f[x][j + wei[x] - k]);
    }
}

int main()
{
    scanf("%lld%lld", &n, &m);
    Clear();
    W[n + 1] = V[n + 1] = 0;
    for(int i = 1; i <= n; i++) scanf("%lld", &W[i]);
    for(int i = 1; i <= n; i++) scanf("%lld", &V[i]);
    for(int i = 1; i <= n; i++)
    {
        scanf("%lld", &d[i]);
        if(d[i] == 0) { d[i] = n + 1; continue; }
        add(d[i], i);
    }
    col[n + 1] = n + 1;
    for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i);
    cnt = 0;
    memset(head, 0, sizeof(head));
    memset(e, 0, sizeof(e));
    for(int i = 1; i <= n; i++)
        if(col[i] != col[d[i]]) add(col[d[i]], col[i]), rd[col[i]]++;
    for(int i = 1; i <= n; i++)
        wei[col[i]] += W[i], val[col[i]] += V[i];
    for(int i = 1; i <= color; i++) if(rd[i] == 0) add(n + 1, i);
    dfs(n + 1);
    printf("%lld", max(0ll, f[n + 1][m]));
    return 0;
}