浅析决策树及其剪枝、集成方法
导读
决策树作为机器学习十大算法之一,具有易理解,可解释性强,使用场景多(包括特征重要性)等,利用提升(Boosting)方法可以构建较好的基准线(baseline),但优化决策树存在许多注意点,比如剪枝(pruning)方法的选择,集成(ensemble)方法的取舍等;本文借鉴了多篇(目前是12篇)博客,包括towarscience、博客园、知乎、简书、machinelearningmastery(强推)、高校ppt等资源,进行初步分析;
决策树实际落地还有许多注意点(选择、取舍等)、优化方法、数学原理等内容,本篇不做深入探讨,另找时间出一篇更深入的博客,希望大家多提意见,一起进步呀。
brief introduction
information
决策树(Decision Tree,以下简称DT),是简单树形结构(tree structure)的基于概率期望值(expected probability)的非线性分类器(nonlinear classifier)(分类超平面类似于折跃函数(folding function)\([1][2]\) );通过(在当前节点(node))不断寻找信息增益(information gain)最大的位置分割特征,生成并(使用分支(branch))连接子节点(leaf nodes)\([1]\) 。
其中需要学习三个数据值:树形状(structure learning)(深度和广度)、决策阈值(decision threshold)、叶节点对应值(classifier results)。(图来源\([1 ]\)
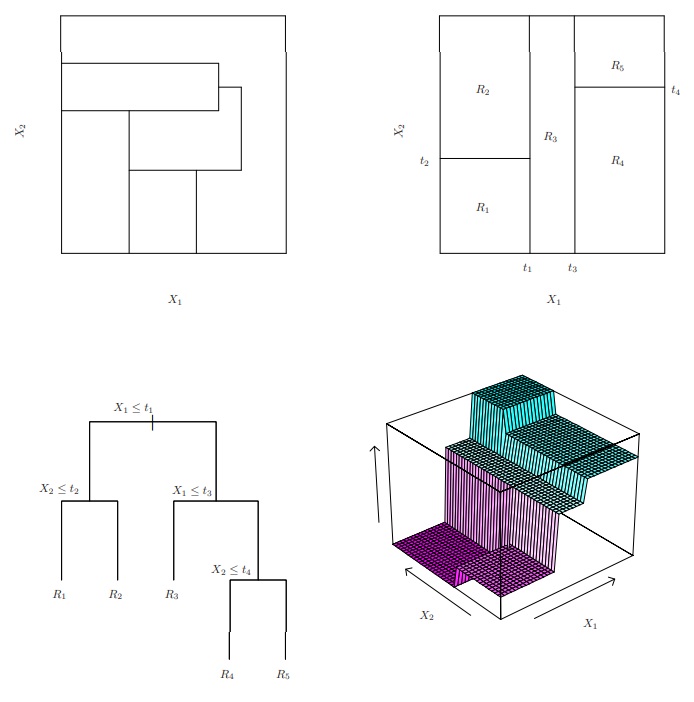
多变量决策树(Multivariate Decision Tree)\([3]\),即使用特征线性组合进行特征分割,以达到“斜划分”;。(图来源\([3]\) )
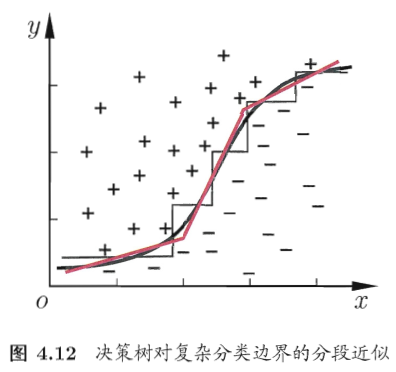
details
属性:简单但可解释性(Interpretability)强,监督学习(supervised learning),非线性分类器(nonlinear classifier),树结构(tree instructure),基于期望概率(expected probability)\([1]\),基于分类信息熵(information entropy)或回归均方误差(Mean Squares Error),不支持在线学习。
求解:分类树:因为要使分类结果的各个叶节点中样本尽可能属于同一类,所以采用信息混乱度衡量(即信息熵),(类似于贪心算法)每一次分割都使信息熵增加最多;回归树:切分连续数据,损失函数为均方误差,基于残差数据拟合多个子树,叠加得到回归决策树\([4]\)。
扩展:决策树极易受到异常数据干扰进而过拟合:
1.采用剪枝(pruning)方法,包括预剪枝(prepruning)和后剪枝(post-pruning)\([3]\) ,方法有设置参数阈值、错误率降低剪枝( Reduced-Error Pruning , REP) 、悲观错误剪枝( Pessimistic Error Pruning, PEP) 、代价复杂度剪枝( Cost-Complexity Pruning, CCP) \([4]\) ;
2.采用集成方法(ensemble methods),包括装袋(bagging)和提升(boosting),方法有随机森林(Random Forest)、梯度提升决策树( Gradient Boosting Decision Tree)等。
entropy
| algorithm | entropy | remarks |
|---|---|---|
| ID3 | information gain | 多叉树,离散特征,偏好类别较多特征 |
| C4.5 | gain-ratio | 多叉树,可连续特征,偏好类别较少特征 |
| CART | gini impurity | 二叉树,分类和回归 |
-
信息熵:集合总体不确定性程度\([6 ]\)
\[\begin{aligned} \H(X)=-\sum_{i=1}^nP_i\log_2{P_i} \end{aligned} \] -
条件熵:已知某个信息下,集合不确定性程度$[6 ] $
\[\begin{aligned} \H(X|Y) &=\sum_{v\in values(Y)}P_{Y=v}\H({X|Y=v})\\ &=\sum_{v\in values(Y)}P_{Y=v}[-\sum_{i=1}^nP_{X=i,Y=v}\log_2{P_{X=i,Y=v}}]\\ \end{aligned} \] -
延伸阅读:卡方自动交互检测(CHi-square Automatic Interaction Detection,CHAID),用于在分类树计算时,执行多级分割;多元自适应回归样条(Multivariate Adaptive Regression Splines,MARS)\([12]\) 。
information gain
-
信息增益:特征\(F\)对数据集\(D\)不确定性减少的程度(包括信息熵和条件熵)
\[\begin{aligned} {\cal{g}}(D,F)&= \H(D)-\H(D|F)\\ \end{aligned} \] -
特点:偏好类别取值数量较多的特征(即类别取值数量更多的特征对集合的信息增益更大)
- 原因:(类别多,可能分类后集合熵更低,此时信息增益更大,但可能出现分类过细而过拟合\([6 ]\)),可能出现的情况,难以通过公式推导证明;
- 解决办法:使用信息增益率;
-
迭代二分法三(The Iterative Dichotomiser 3,ID3)使用
- 优缺点:每次仅搜索空间一部分,速度快,测试数据少,形式简单(不分割特征值),深度小;但无法处理连续数值和缺失数据\([8]\) ;
information gain-ratio
-
信息增益率:特征\(F\)对数据集\(D\)的信息增益除以特征\(F\)的信息熵(即注重有效信息增益)
\[\begin{aligned} {\cal{g_r}}(D,F)&= \]\end{aligned}
\[ \]- 原因:(类别少,必然使分类后惩罚系数(即特征信息熵)更小,此时信息增益率更大,但可能出现分类粗糙而欠拟合\([6]\) )
- 解决办法:先选择信息增益高于平均的部分,从中,再选择信息增益率最高的\([6][9]\) ;
-
C4.5使用
- 优缺点:支持对连续数据进行离散化(下面详细讨论),可以对缺失数据进行填充(下面详细讨论),K次迭代交叉验证,可以使用剪枝方法;但速度较慢,计算复杂(多叉树、对数运算、排序)\([8]\) ;
gini impurity
-
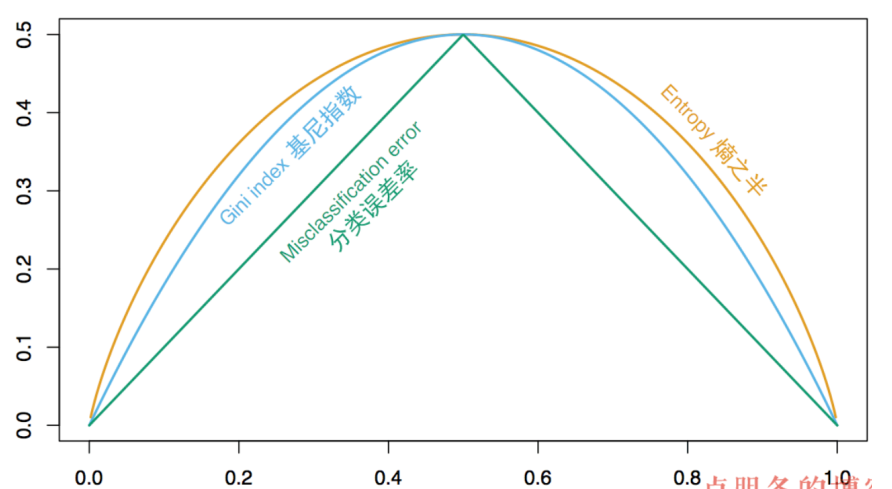
基尼不纯度:从数据集 D 中随机抽取一个样本,其类别被错分的概率 (数值等于随机抽取两个样本,类别不一致的概率)\([4][9]\) ;
\[\begin{aligned} {\cal{Gini}}(p) &=\sum_{k=1}^Kp_k(1-p_k)\\ &=1-\sum_{k=1}^Kp_k^2 \end{aligned} \] -
特点:物理含义接近C4.5,更便于计算\([4]\)
![]()
-
分类与回归树(Classification And Regression Tree)分类时使用:
- 优缺点:计算简单,几乎不需要预处理\([7]\);需要生成多个决策树(sequence of decision trees),使用代理特征分割(surrogate splits)时计算量爆表\([9]\)
MSE/LSD
-
均方误差(Mean Squares Error,MSE)\([4]\) : 计算每个序列间隔(序号:x.5,即两个连续数据点的中间)拆分的子序列之最优输出(均值),在计算最优输出与真实数据间的平方误差,迭代选择最小MSE;最后融合多个子树;
-
最小二乘偏差(Least Squares Diviation,LSD)\([7]\) :在均方误差首次计算后,迭代选择最小LSD,减少计算量;
-
分类与回归树(Classification And Regression Tree)回归时使用:
- 优缺点:回归中解释性强,能回归高度非线性;但因变量和自变量之间的关系无法很好逼近\([12]\) 。
pruning
机器学习笔记(6)——C4.5决策树中的剪枝处理和Python实现,决策树系列(二)——剪枝,决策树的剪枝问题,
pre-pruning
- 可以有效提高泛化能力才进行下一步分割,减少计算;但容易产生“视界局限”,即会忽略下下一步(已被舍弃)\([2]\) ,且需要准备测试集:
- 信息熵增最小阈值
- 广度/深度最大阈值
- 叶节点最少样本阈值
- 性能提高最小阈值(常用)
- 留出法:留出部分数据作为测试集,每一步分割,都比较测试集在分割前后的精度,有性能提升则进行分割(即性能提高最小阈值为0%)\([3]\) 。
post-pruning
-
使树充分生长,然后自底而上消除能提高泛化能力的子树,克服“视界局限”;计算量大不适用于大数据量\([2]\) ,可以不需要测试集:
- 错误率降低剪枝(REP)
- 悲观错误剪枝(PEP)
- 代价复杂度剪枝(CCP)
-
错误率降低剪枝(REP):留出测试集,自下而上比较测试集在叶节点上下精度,有必要即删除(类似于预剪枝-留出法的反向)(用于ID3)\([11]\)
-
悲观错误剪枝(PEP):自上而下比较在节点上(带惩罚项\(\epsilon\),也是“悲观”的原因)的错误率和标准误差,如果树错误率大于节点错误率-标准误差,执行剪枝(用于C4.5)\([11][13]\) ;充分使用数据准确率高,但容易剪枝过度(自上而上的“视界局限”)甚至剪枝失败。
\[\begin{aligned} &E(n^+)\geq E(n)-S{\large(}E(n^+){\large)} \\ define: &E(n^+)=\sum_{i=1}^m(e_i+\epsilon)\\ &E(n)=e+\epsilon\\ &S{\large(}E(n^+){\large)} =\sqrt{np(1-p)}\\ &\epsilon=0.5, p:E(n^+)/n\\ &m:叶节点数量, n:总样本数\\ &n^+:带节点n的树,n:节点n \\ \end{aligned} \] -
代价复杂度剪枝(CCP):计算全部节点的剪枝系数,循环查找最小剪枝系数,从而获得多个剪枝后的树(决策树序列\(T_k\)),交叉验证选择最优树(用于CART)\([13]\) ;避免剪枝过度,但计算量较大。
\[\begin{aligned} \alpha &=\frac{\R(t)-\R(T)}{m-1}\\ &=\frac{r_e(t)\cdot p_{all}(t)-\sum^m\R(T_i)}{m-1}\\ &=\frac{r_e(t)\cdot p_{all}(t)- \sum^mr_e(T_i)\cdot p_{all}(T_i)}{m-1}\\ define:\qquad &r_e(t):节点t错分样本在节点样本占比\\ &p_{all}(t): 节点t样本在全部样本占比\\ &m:叶节点数量\\ &T_i:节点t为根的树T的叶节点\\ \end{aligned} \]
value processing
continuous value\([4][9]\)
- 区间划分(bi-partition):特征\(F\in[a,d]\),(启发式方法)分割为多个空间\(F_1\in[a,b),F_2\in[b,c),F_3\in[c,d)\) (C4.5);
- 取值划分:特征\(F\),取值\([1,2,3,4,5]\),在取值间隙(如\([1,2,3]/[4,5]\))划分,且可连续划分(即视为类别较多的离散值)(CART);
missing value\([3][9]\)
-
缺失特征信息增益率:在非缺失值上进行分裂,计算信息增益率,然后根据非缺失值的占比在计算出来的信息增益率前加入比值系数\([9 ]\)
\[\begin{aligned} &g(D,F^+)=\frac{len(F^+)}{len(F)}g(D_F^+,F^+) \\ define:\qquad &F^+:特征中非缺失值\\ &D_F^+:集合中非缺失值集合\\ \end{aligned} \] -
最优特征缺失:使用样本权重将缺失值按照权重切分划分到不同的节点中 \([9]\)
ensemble model
集成方法是重要算法,与决策树同一地位,后续会另开一篇续写Bagging、Boosting(AdaBoost、XGBoost)等;
推荐阅读:深度随机森林(Deep Random Forest),作者周志华,3 Reasons to Use Random Forest Over a Neural Network–Comparing Machine Learning versus Deep Learning,DPP(determinant point process),Determinantal point processes for machine learning;
这些模型也是集成模型(想不到吧)
- dropout/dropconnect
- bayesian model
- denoising autoencoder
bagging
使用同一份样本,有放回随机采样(bootstrap aggregating),并行构建K个模型,最后投票决定\([4]\) ;(单个模型拟合过强,容易过拟合)
- 随机森林(Random Forest,RF):(通过提高子集多样性(diversity))有效减少方差(variance reduction)(\(\frac{\sigma^2}{K}\)),降低错误风险,有效处理高维数据,处理缺失数据并保持准确性;但(回归)取值无法精确;\([14]\)
![]()
boosting
使用均等分割的样本,基于概率近似正确(Probability Approximatly Correct),逐步训练K个模型,最终得到最终模型(\(f_K(x)=\sum_{m=1}^Kh_m(x)\))\([4]\) ;(单个模型拟合过弱,容易欠拟合)Decision Tree vs Random Forest vs Gradient Boosting Machines: Explained Simply,Boosting and AdaBoost for Machine Learning;
| 外循环 | 内循环 | 公式 |
|---|---|---|
| 初始化模型 | \(f_0(x)=0\) | |
| 迭代K次(生成K个弱模型) | for i in range(1,K) | |
| 初始损失 | \(l_i=L(y,f_{i-1}(x))\) | |
| 拟合损失, 生成当前学习器 |
\(h_i(x)=classifier_i(x,l_i)\) | |
| 本轮损失 | \(l_i=L(y,f_{i-1}(x)+h_i(x))\) | |
| 生成新模型 | \(f_i(x)=f_{i-1}+h_i(x)\) | |
| 得到提升树 | \(f_K(x)\) |
- 梯度提升决策树(Gradient Boosting Decision Tree,GBDT)(又叫Multiple Additive Regression Tree,MART):以梯度下降的最速下降近似方法,即以损失函数负梯度拟合决策树,此处是残差(\(y-f_{i-1}(x)\)) \([4]\) ;
| 外循环 | 内循环 | 公式 |
|---|---|---|
| 初始化模型 | \(f_0(x)=\arg\min_c\sum_{i=1}^NL(y_i,c_0),c_0=mean(labels)\) | |
| 迭代K次 | for i in range(1, K) | |
| 损失 | \(l_i=-[\frac{\partial L(y,f_{i-1}(x))}{\partial f_{i-1}x}]\) | |
| 拟合损失的学习器 | \(h_i(x)=classifier_i(x,l_i)\) | |
| 输出值 | \(c_i=\arg\min_c\sum_{x_i\in \R_i}L(y_i,f_{i-1}(\hat{x})+c_{i-1})\) | |
| 生成新模型 | \(f_i(x)=f_{i-1}+lr\cdot\sum_{j=1}^Jc_iI\) |
#reference links
[1].Stanford,课程:Data mining and analysis,Lecture 19: Decision trees;
[2].百度百科,决策树;
[3].机器学习(西瓜书),作者:周志华,第四章第五节;
[4].贪心科技,课程:自然语言训练营,回顾-决策树;
[5].towardscience,作者:Anuja Nagpal,Decision Tree Ensembles- Bagging and Boosting;
[6].博客园,作者:张小呱,决策树--信息增益,信息增益比,Geni指数的理解;
[7].towardscience,作者:Diego Lopez Yse,The Complete Guide to Decision Trees;
[8].新浪博客,作者:杨童,【周记2】C4.5算法来源;
[9].知乎,作者:马东什么,决策树 ID3 C4.5 cart 总结;
[10].towardscience,作者:Lorraine Li, Classification and Regression Analysis with Decision Trees;
[11].博客园,作者:学会分享~,决策树系列(二)——剪枝;
[12.].towardscience,作者:Nagesh Singh Chauhan:,Decision Tree Algorithm — Explained;
[13].博客园,作者:DreamFaquir,决策树-剪枝算法(二);
[14].towardscience,作者:Neil Liberman,Decision Trees and Random Forests;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号