整除分块总结
整除分块
一些引理
引理1
\(\large \forall \ a,b,c\in Z,\left \lfloor\dfrac{a}{bc}\right\rfloor=\lfloor\dfrac{\lfloor\dfrac{a}{b}\rfloor}{c}\rfloor\)
略证:
\(\large \dfrac{a}{b}=\lfloor\dfrac{a}{b}\rfloor+r\ \ (0\le r< 1)\)
\(\large \to \ \lfloor\dfrac{a}{bc}\rfloor=\lfloor\dfrac{a}{b}\cdot \dfrac{1}{c}\rfloor=\lfloor\dfrac{1}{c}(\lfloor\dfrac{a}{b}\rfloor+r)\rfloor=\lfloor\dfrac{\lfloor\dfrac{a}{b}\rfloor}{c}+\dfrac{r}{c}\rfloor=\lfloor\dfrac{\lfloor\dfrac{a}{b}\rfloor}{c}\rfloor\)
引理2
\(\large \forall \ n\in N^{+},|\{\lfloor\dfrac{n}{d}\rfloor|d\in N^{+},d\le n\}|\le \lfloor2\sqrt{n}\rfloor\)
- 人话:对于所有的正整数来说,其除 \(1,2,3,...n\) 下取整的元素最多 \(\lfloor2\sqrt{n}\rfloor\) 个。
略证:
对于 \(d\le \lfloor\sqrt{n}\rfloor,\lfloor\dfrac{n}{d}\rfloor\) 有 \(\lfloor\sqrt{n}\rfloor\) 种取值。
对于 \(d> \lfloor\sqrt{n}\rfloor,\) 有 \(\lfloor\dfrac{n}{d}\rfloor\le \lfloor\sqrt{n}\rfloor,\) 也有 \(\lfloor\sqrt{n}\rfloor\) 种取值。
相加即可。
时间复杂度证明
对于任意一个正整数 \(n\) ,\(\lfloor\dfrac nd \rfloor\) 的种类数为 \(O(\sqrt{V})\) ,因此整除分块的时间复杂度为 \(O(\sqrt{n})\) 。
按照 \(d\) 的大小来分类讨论:
当 \(d\le \sqrt{n}\) 时,因为 \(d\) 只有 \(\sqrt n\) 种取值,所以与之对应的函数 \(\lfloor\dfrac nd\rfloor\) 也最多只有 \(\sqrt n\) 种取值。
当 \(d>\sqrt n\) 时,\(\lfloor \dfrac nd\rfloor\le \sqrt n\) ,所以不同的 \(\lfloor \dfrac nd \rfloor\) 最多只有 \(\sqrt n\) 个。
综上,\(\lfloor\dfrac nd \rfloor\) 的种类数为 \(O(\sqrt{V})\)
常见应用
当出现求和式子包含 \(\large \lfloor\dfrac ni\rfloor\) 时,我们可以对于每一个 \(i\) 找到最大的 \(j\) 使得 \(\large \lfloor\dfrac ni\rfloor=\large \lfloor\dfrac nj\rfloor\)
整除分块后,所求的函数和可以使用前缀和进行优化
整除分块的端点
注意:计算出的块的 \(R\) 要判断是否超过上界。
向下取整
端点计算
如果我们按照 \(\lfloor \dfrac n d\rfloor\) 来分块。
那么就是寻找最大的 \(k\) 满足:\(\lfloor\dfrac nL\rfloor=\lfloor \dfrac n{L+k}\rfloor\)
设 \(\lfloor\dfrac nL\rfloor=\lfloor \dfrac n{L+k}\rfloor=x\)
根据带余除法的定义,我们可以设 \(n=xL+p=x(L+k)+q\)
因此 \(k=\lfloor\dfrac {p-q}x\rfloor\le \lfloor\dfrac px\rfloor=\left\lfloor\dfrac {n\%L}{\lfloor\dfrac nL\rfloor}\right\rfloor\)
所以当 \(q=0\) 时,有 \(q_{\max}=\left\lfloor\dfrac {n\%L}{\lfloor\dfrac nL\rfloor}\right\rfloor\)
此时 \(R=L+q_{max}=L+\left\lfloor \dfrac{n-\lfloor\dfrac nL\rfloor\cdot L}{\lfloor\dfrac nL\rfloor}\right\rfloor=\left\lfloor\dfrac n{\lfloor\dfrac nL\rfloor}\right\rfloor\)
代码
一般的整除分块的实现,通过 \(l,r\) 来实现分块。
这里是求 \(\large \sum\limits_{i=1}^m{\lfloor\dfrac ni\rfloor}\) 的整除分块代码实现。
for(int l=1,r;l<=m;l=r+1){//为了区分,这里m是上界
r=n/(n/l);//根据引理3得到r,按道理来说还得加上特判范围r<=m
ans+=(r-l+1)*(n/l);//r-l+1是这段区间的个数,(n/l)就是这段区间共同的值
}
多项式向下取整
按照 \(\lfloor \dfrac n{ad+b}\rfloor\) 来分块。
端点计算
如果按照 \(\lfloor \dfrac n{ad+b}\rfloor\) 来分块:
那么就是寻找最大的 \(k\) 满足 \(\lfloor \dfrac n{aL+b}\rfloor=\lfloor \dfrac n{aL+ak+b}\rfloor\)
设 \(\lfloor \dfrac n{aL+b}\rfloor=\lfloor \dfrac n{aL+ak+b}\rfloor=x\)
根据带余除法,可以设 \(n=x(aL+b)+p=x(aL+ak+b)+q\)
因此 \(q=p-xak\Rightarrow k=\lfloor \dfrac {p-q}{ax}\rfloor\le \lfloor \dfrac p{ax}\rfloor=\lfloor\dfrac{n\%(aL+b)}{a\lfloor\dfrac n{aL+b}\rfloor}\rfloor\)
所以当 \(q=0\) 时,有
\(R=L+q_{max}=L+\lfloor\dfrac{n-\lfloor\dfrac n{aL+b}\rfloor\cdot (aL+b)}{a\lfloor\dfrac{n}{aL+b}\rfloor}\rfloor=\lfloor\dfrac n{a\lfloor\dfrac n{aL+b}\rfloor}-\dfrac ba\rfloor\)
代码
这里是求 \(\large \sum\limits_{i=1}^m{\lfloor\dfrac n{ai+b}\rfloor}\) 的整除分块代码实现。
for(int l=1,r;l<=m;l=r+1){//为了区分,这里m是上界
r=(int)floor((1.0*n)/(1.0*a*floor((n)/(1.0*a*l+b)))-1.0*b/a);//根据推导的结果得到r,按道理来说还得加上特判范围r<=m
ans+=(r-l+1)*(int)floor(1.0*n/(a*l+b));//r-l+1是这段区间的个数,(int)floor(1.0*n/(a*l+b))就是这段区间共同的值
}
平方向下取整
按照 \(\lfloor \dfrac n{d^2}\rfloor\) 分块。
端点计算
如果按照 \(\lfloor \dfrac n{d^2}\rfloor\) 分块:
那么就是寻找最大的 \(k\) 满足 \(\lfloor \dfrac n{L^2}\rfloor=\lfloor \dfrac n{(L+k)^2}\rfloor\)
设 \(\lfloor \dfrac n{L^2}\rfloor=\lfloor \dfrac n{(L+k)^2}\rfloor=x\)
根据带余除法,可以设 \(n=xL^2+p=x(L+k)^2+q\)
因此 \(k=\left\lfloor \sqrt{L^2+\dfrac {p-1}x}\right\rfloor-L\le \left\lfloor \sqrt{L^2+\dfrac px}\right\rfloor-L=\left\lfloor \sqrt{L^2+\dfrac{n\%L^2}{\lfloor \dfrac n{L^2}\rfloor}}\right\rfloor-L\)
所以当 \(q=0\) 时,有:
\(R=L+q_{max}=L+\left\lfloor \sqrt{\dfrac{n}{\lfloor \dfrac n{L^2}\rfloor}}\right\rfloor-L=\left\lfloor \sqrt{\dfrac n{\lfloor \dfrac n{L^2}\rfloor}}\right\rfloor\)
代码
这里是求 \(\large \sum\limits_{i=1}^m{\lfloor\dfrac n{i^2}\rfloor}\) 的整除分块代码实现。
for(int l=1,r;l<=m;l=r+1){//为了区分,这里m是上界
r=(int)floor(sqrt(1.0*n/floor(1.0*n/(l*l))));//根据推导的结果得到r,按道理来说还得加上特判范围r<=m
ans+=(r-l+1)*(int)floor(1.0*n/(l*l));//r-l+1是这段区间的个数,(int)floor(1.0*n/(l*l))就是这段区间共同的值
}
向上取整
端点计算
按照 \(\lceil \dfrac nd\rceil\) 分块:
考虑转化为向下取整。
如果 \(d \nmid n\) ,那么 \(\lceil \dfrac nd\rceil=\lfloor \dfrac nd \rfloor +1=\lfloor \dfrac nd +1\rfloor =\lfloor \dfrac {n+d}d\rfloor=\lfloor \dfrac {n+d-1}d\rfloor\)
如果 \(d\mid n\) ,那么 \(\lceil \dfrac nd\rceil =\lfloor \dfrac nd\rfloor=\lfloor \dfrac{n+d-1}d\rfloor\)
因此对于任意 \(d\) ,有 \(\lceil \dfrac nd\rceil=\lceil \dfrac{n+d-1}d\rceil\)
即按照 \(\lfloor \dfrac{n+d-1}d\rfloor\) 分块
设当前左端点为 \(L\) ,寻找最大的 \(k\) 使得 \(\lfloor \dfrac{n+L-1}L\rfloor=\lfloor\dfrac{n+L+k-1}{L+k}\rfloor\)
那么设 \(\lfloor \dfrac{n-1}L\rfloor=\lfloor\dfrac{n-1}{L+k}\rfloor=x\)
根据带余除法,可以设 \(n-1=xL+p=x(L+k)+q\)
因此 \(q=p-xk\Rightarrow k=\lfloor\dfrac{p-1}{x}\rfloor\le \lfloor\dfrac px\rfloor=\lfloor\dfrac{(n-1)\%L}{\lfloor\dfrac{n-1}{L}\rfloor}\rfloor\)
当 \(q=0\) 时, \(R=L+q_{max}=L+\lfloor\dfrac{n-1-\lfloor\dfrac{n-1}{L}\rfloor\cdot L}{\lfloor\dfrac{n-1}{L}\rfloor}\rfloor=\lfloor\dfrac{n-1}{\lfloor\dfrac{n-1}{L}\rfloor}\rfloor\)
代码
暂无。
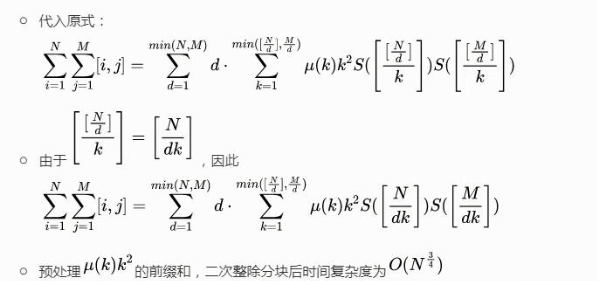
二次整除分块

时间复杂度


代码
暂无。
应用
求余数和

求gcd和

求lcm和