机器学习单词记录--07章logistic回归
###分类
Transaction 交易
Fraudulent 欺诈
0 is the negative class :0是负拷贝类
分类 0 、 1
通常用1表示我们需要找的,0表示没有
假设函数
Threshold 阈值
Horizontal 横轴
在分类上y是0或1 ,但在线性回归问题上y可能远大于1远小于0,所以logistic regression出来了,它就是叫做logistic回归(实际上就是一种分类算法)的算法。
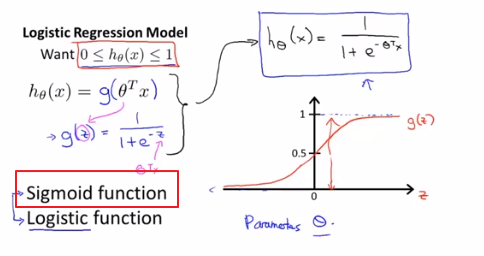
#####假设陈诉
Logistic函数(sigmoid function=logistics function 指代某个函数)
Given this hypothesis representation,what we need to do ,as before ,is fit the parameters theta to our data.
有了假设函数后,我们要做的和之前一样,就是用参数θ拟合我们的数据。
Hypothesis will then let us make predictions .
假设函数会帮我们作出预测
#####决策界限
Decision boundary 决策边界
G of z 代表的是g(z)
We will predict Y equals 1,whenever theta transpose axis greater than or equal to 0.And we will predict Y is equal to zero whenever theta transpose X is less than zero.
当θTX大于等于0时预测Y为1,当它小于0时就预测Y为0.

So long as we’ve given my parameter vector θ,that defines the decision boundary which is the circle.
只要给定了参数向量θ,圆形的决定边界就确定了。
But the training set is not what we use to define decision boundary .The training set may be used to fit the parameters θ.Once you have the parameters θ,that is what defines the decision boundary.
我们不是用训练集来定义的决策边界,我们训练集来你和参数θ。但是一旦你有了参数θ,它就确定了决策边界。

This line there is called the dicision boundary.
我们把这条线叫做决策边界
Actually,this line corresponds to this set of points.
这条决策边界实际上对应一系列的点(θTX)。
Visualization 可视化
This decision boundary and a region where we predict 1 equals versus Y equals 0.That’s a property of the hypothesis and of the parameters of the hypothesis,and not a property of the data set.
这条决策边界和我们预测y=1和y=0的区域。他们都是假设函数的属性,取决于其参数,他不是数据集的属性。

By adding these more complex polynomial terms to my features as well,I can get more complex decision boundaries that don’t just try to separate the positive and negative examples with a straight line.
通过在特征中增加这些复杂的多项式,我可以得到更复杂的决定边界,而不只是用直线分开正负样本。
###代价函数
How to fit the parameters theta
如何你和logistic回归
Squared error term 平方误差项
The cost function is 1/m times the sum over my training set of this cost term here.
代价函数是cost项在训练集范围的求和

If we could minimize this cost function that is plugged into J here,that will work okey.But if we use this particular cost function ,this would be a non-convex function of the parameters theta.
如果我们可以最小化函数J里面的这个代价函数,它也能工作。但是如果我们使用这个代价函数,他会变成参数θ的非凸函数。

For logistic regression ,this function H here has a non linearity.J of θ may have many local optima 。
对于logistic回归来说,H函数是非线性的(因为是θTX相关的函数)。J(θ)可能有许多的局部最优解----这就是一个非凸函数。
If you were to run gradient descent on this sort of function,it is not guaranteed to converge to the global mininum.
如果你把梯度下降法用在一个这样的函数(指的就是上面的非凸函数),不能保证它会收敛到全局最小值。
所以我们希望我们的代价函数J(θ)是一个凸函数,a single bow-shaped function一个单弓形函数,如果是一个纯纯的凸函数,使用梯度下降法就能保证会收敛到全局最小值。
让J(θ)代价函数变为非凸函数的原因是我们使用sigmod函数来定义H,里面有平方项。So what we would like to do
Is instead come up with a different function that is convex and so that we can apply a great algorithm like gradient descent and be guaranteed to find a global minimum.【所以我们要用别的凸函数,以便我们可以更好的使用像梯度下降的算法并且得到全局最小值】
penalty 惩罚
Blow up 激增
Infinite 无限
###简化代价函数和梯度下降函数
Compress ... into ... 压缩、合并
Derive 推导
Bring the minus sign outside 把负号放在外面
Maximum likelihood estimation 极大似然值
The way we’re going to minimize the cost function is using gradient descent.
最小化代价函数的方法是使用梯度下降法。
We repeatedly update each parameter by updating it as itself minus a learning rate alpha this derivative term.
我们要反复更新每个参数,就是用他自己减去学习率α乘以后面的导数项。
假设函数的定义发生了变化,所以和线性回归的梯度下降是完全不一样的。
Even though the update rule looks cosmetically identical,because the definition of the hypothesis changed,this is actually not the same thing as gradient descent for linear regression.
即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以梯度下降和logistic回归是不一样的算法。
Monitor 监视
Converge 收敛

Features scaling can help gradient descent converge faster for linear regression.
特征缩放可以提高梯度下降的收敛速度。
特征缩放统一适用于logistic回归。
###高级优化
Last 上一个、最后
Advanced optimization algorithms 高级优化算法
Gradient descent repeat perform the following update.
梯度下降算法做的就是反复执行这些,来更新θ参数。
梯度下降并不是唯一的minimize the cost function【最小化代价函数的】算法,还有别的advanced,sophisticated优化算法。
Advanced numerical computing 高等数值
Property 特性
Manually 手动

These algorithms is that given these the way to compute the derive and a cost function,we can think of these algorithms as a clever inner-loop called a kine search algorithm .
这些算法的一种思路是,给出计算导数项和代价函数的方法。想象这些算法有一个叫做线搜索算法的智能内循环,
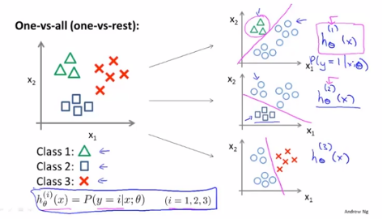
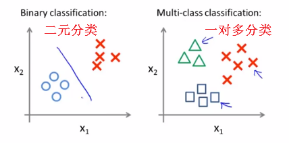
###多元分类:一对多
One-versus-all 一对多
Y can take on a small number of discrete values
Y可以取一些离散值
Positive ,negative