机器学习单词记录--05章多变量线性回归
Liner regression 线性回归
Multiple variables 多个变量
Original version 原始的版本
A single feature 一个特征向量
Our form of our hypothesis
Notation 符号、记法
Subscript下划线
Denote the number of example 代表样本的数量
Lowercase 小写的
Superscript 上标
M-dimensional features vector n维向量
x^2 代表第二个n维向量 x^2_3 代表第二个n维向量的第3个特征值
Form形式
Simple representation 简单的表达方式
A particular setting of our parameters 设置的参数
Example i 第i个样本
Inner products of vectors 向量内积
Transpose 转置
A row vector 行向量
Compact form 紧凑的方式
Multivariate linear regression 多元线性回归
The form of the hypothesis for linear regression with multiple features or with multiple variables :

How to fit the parameters of that hypothesis ?
Convention 惯例
N separate parameters n个独立参数
Sum of square of error term 误差项的平方和--cost function代价函数
Derivative 导数
Partial derivative 偏导数


Practical tricks 使用的技巧
Make gradient descent work well in practice
Feature scaling 特征缩放?
-- make gradient descent run much faster and converge in a lot fewer iterations让梯度下降得更快,让收敛所需的迭代次数也更少
No1--dividing by the maximum除以最大值 No2--Mean normalization 均值归一化 【但是不会对X0操作,因为它是1】
Different features take on similar ranges of values , Gradient descents can converge more quickly
特征值如果能在相似的范围内,梯度下降法能更快地收敛
Plot the contours of the cost function J(θ) 画出代价函数J的等值线
Skew 歪斜
Elliptical shape 椭圆形状
Tall and skinny ellipses 又瘦又高的椭圆形
Oscillate back and forth 来回波动
Global minimum 全局最小值
contour等值线
椭圆值越细高、梯度下降就会越久、越曲折、越缓慢才能找到全局最小值的路
By scale the features,they take on similar ranges of values 通过特征缩放,它们的值的范围变得相近
Trajectory 轨道
当我们执行特征缩放时,我们通常的目的是把特征的取值约束到-1到+1的范围内。但这个-1,+1的值也可以被你确定为0,+3都差不了多少,但是如果还有一个特征是在-100,+100 OR -0.00001,+0.0000001之间的,那么就不得不做些什么了,就是不要太大也不要太小的意思。
Take-home message 总的来说
Mean normalization 均值归一化


Learning rate 学习率
Update rule更新规则
Debugging 调试
Tips小技巧
梯度下降的作用是找到一个合适的θ,并且希望它能够最小化代价函数J(θ)
The J of theta decrease after every iteration 每一步迭代之后J(θ)都应该下降
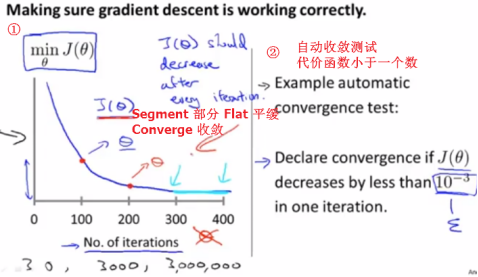
Judge whether or not gradient descent has converged 判断梯度下降算法是否已经收敛
It turns out to be very difficult to tel in advance how many iterations gradient descent needs to converge ,and is usually by plotting this sort of plot .Plotting the cost function as we increase the number of iterations.画出代价函数岁迭代部署增加的变化曲线来判断梯度下降算法是否已经收敛
Automatic convergence test 自动收敛测试
choose what this threshold is pretty difficult 选择一个合适的阈值很难
通常来说随着迭代次数的增加,代价函数是变小的,所以还能检测算法是否正常工作。
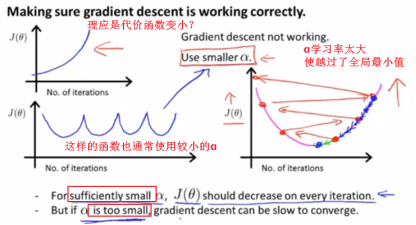
A figure like this ,usually means that you should be using a learning rate alpha .If J of theta is actually increasing ,the most common cause for that is if you’re trying to minimize the function that maybe looks like this.But if your learning rate is too big, then if you start off there ,gradient descent may overshoot the minimum.
这样的曲线,通常表示你应该使用一个更小的学习率α。如果J(θ)在上升,最常见的原因就是你在尝试最小化这样的函数,但是你从这里开始,梯度下降算法可能冲过了最小值,于是会得到越来越大的代价函数值。

If your learning rate alpha is small enough ,then j of theta should decrease on every single iteration ,但是如果学习率α太小收敛速度也会很慢
Polynomial regression 多项式回归
Use the machinery of linear regression to fit very complicated ,even very non-linear functions.
Sometimes a new feature means a better model 例如 房屋的宽和长OR房屋的面积
Quadratic function 二次函数
Cubic function 三次函数
Third-order term 三次的式子
The machinery of multivariant linear regression 多元线性回归的方法
Feature scaling 特征缩放-----因为特征值的范围太大
You have choice in what features to use,such as that instead of using to frontage and the depth of the house,maybe ,you can multiply them together to get a feature that captures the land area of a house
有许多特征,你可以决定使用什么特征
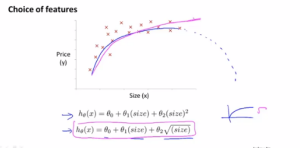
Algorithms for automatically choosing what features to used .自动选择要使用什么特征的算法
Normal equation正规方程
The optimal value of the parameters theta θ的最优解
我们一直在使用的线性回归的算法--梯度下降法,为了求的最优的代价函数J(θ)【就是使得代价函数J(θ)最小化的θ值】,我们不断的迭代。
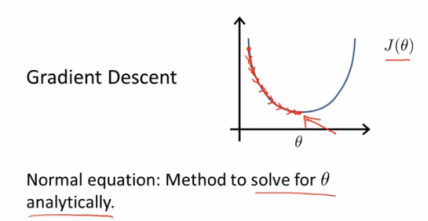
The normal equation would give us a method to solve for theta analytically ,so that rather than needing to run this iterative algorithm,we can instead just solve for the optimal value for theta all at one go.
正规方程给我们提供一种求θ的解析解法,所以我们不再需要运行迭代算法,只需要一次求解就能得到θ的最优解。
Calculus微积分
如果是一个θ参数,则求导将导函数置零,得到θ。
但通常是多个θ,则多次对θi求偏导,然后把它们全部置零,得到θi。
Take the partial derivative of J with respect to every parameter of θ_J in turn,and then ,to set all of these to 0.
逐个对参数θ_J求偏导,然后把它们全部置零

Involved 复杂
Implement this process 实现这个过程
Alertnatively 换个方式说
Equivalently 等价地
求解使得代价函数最小化的θ
Constuct a matirx called X 构建一个矩阵X------design matrix 设计矩阵
Constuct a vector called Y 构建一个向量y
X transpose X inverse times X transpose y 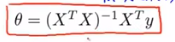

通用的表达式:

The formula gives you the optimal value of θ 这个式子给出最优的θ值
Command 命令
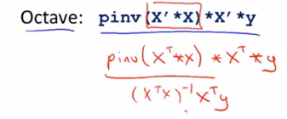
如果使用normal equation method正规方程法,那么就不需要对特征值进行特征缩放feature scaling了
但如果你使用gradient descent梯度下降法,那么特征缩放仍然很重要
Where should you use the gradient descent ,and when should you use the normal equation method?
你何时应该使用梯度下降法,而何时应该使用正规方程法

Gradient descent:~1学习率 α--- 需要尝试多次不同的α才能确定下来--extra work and extra hassle 额外的工作和麻烦 2 需要多次的迭代iterations ~即便有很多的特征值也能运行得很好
Normal equation:~1不需要选择α 2也不需要迭代----不需要画出J(θ)的曲线来检查收敛性 ~如果特征值太多,X矩阵的维度dimension会很大
所以如果是一万及以上的特征值数量,用梯度下降;反之用正规方程。
Sophisticated learning algorithm 复杂的学习算法
在一些复杂的学习算法中,正规方程法可能不适用,但是梯度下降还是能很好的处理的
Classification algorithm 分类算法 --like logistics regression algorithm 逻辑回归算法
Non-invertibility 不可逆性
Non-invertible matrices 不可逆矩阵
Optional material 选学材料
Singular 奇异
Degenerate matrices 退化矩阵
Pseudo-inverse 伪逆
Inverse 逆
Redundant features 多余的特征
Rounded to two decimals 四舍五入到两位小数
Regularization 正则化
Look at your features ,and see if you have redundant features .And if so,keep deleting the redundant features until they are no longer redundant.
看你的特征值里,看是否有一些多余的特征。如果有多余的就删掉直到没有多余的为止。

Submission system 提交系统
Desktop 桌面


