机器学习十讲——第七讲学习总结

机器学习的优化目标

最小化损失函数：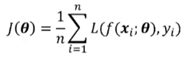

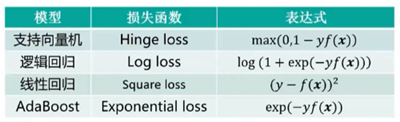
模型——损失函数——表达式：

 

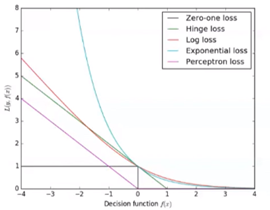
图示：

　　方法

梯度下降：

batch梯度下降：使用全部训练集样本，计算代价太高（n~10^6）

mini-batch梯度下降：随机采样一个子集（m~100或1000），随后使用如下公式：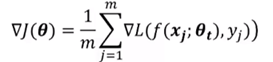

mini-batch是无偏估计。更大的批量会减小梯度计算的方差。

随机梯度下降SGD：

使用mini-batch计算出结果后再根据梯度下降法的公式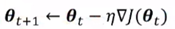：去更新参数，下一步再随机采样子集，重复该操作。此方法称为随机梯度下降（SGD）。

因此有说法：mini-batch是SGD的推广，通常所属SGD即是mini-batch。

因为是训练一次样本更新一次参数，所以梯度下降时通常呈振荡的形式，但大方向上还是下降趋势：

 

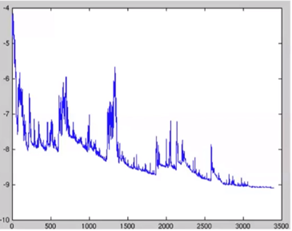
在SGD中学习率的设定是关键。

理论上保证SGD收敛的充分条件： 。因此需要随着迭代次数的增加降低学习率。

设定学习率的方法：

 

梯度下降在实际应用中的问题

病态条件：

右图：假设周边都是悬崖，那么在进行梯度下降算法时会出现垂直下降的情况。

局部最小与全局最小：

 

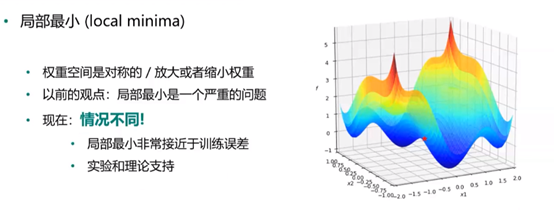
右图所示，直观可以看出最小值在第三个凹处，然而在实际算法中根据设定起点不同，得到的“最小值”可能不是全局最小。

鞍点：

梯度为0，Hessian矩阵同时存在正值和负值；Heissan矩阵的所有特征值为正值的概率很低；对于高维情况，鞍点和局部最小点的数量多。如图所示：

在使用二阶优化算法会有问题。