poj2018 Best Cow Fences[二分答案or凸包优化]
首先暴力很好搞,但是优化的话就不会了。放弃QWQ。
做法1:二分答案
然后发现平均值是$ave=\frac{sum}{len}$,这种形式似乎可以二分答案?把$len$移到左边。
于是二分$ave$,去找数列有没有区间和大于等于其$len$乘以$ave$的,然后卡住了。。
有一个很巧的转化,把每个数都减去一个$ave$,然后任意区间和就相当于把$ave$累加了$len$次。
于是乎只要看区间和$S-len*ave$是否大于等于0就可以了。
存在这样一个区间就说明$ave$可以更大,否则要小。查找存在性是一个简单的前缀和dp。
$O(nlogn)$。
poj精度死活卡不过去。
看来技巧还不够。
于是一气之下把所有double型全换成long long,也就是把小数点后五位通通看成整数,然后运算,最后除以100。
唉。
启示:关于平均数的题目很多时候都是用二分答案处理的。因为是分数形式。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define dbg(x) cerr << #x << " = " << x <<endl 7 using namespace std; 8 typedef long long ll; 9 typedef double db; 10 typedef pair<int,int> pii; 11 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 12 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 13 template<typename T>inline char MIN(T&A,T B){return A>B?(A=B,1):0;} 14 template<typename T>inline char MAX(T&A,T B){return A<B?(A=B,1):0;} 15 template<typename T>inline void _swap(T&A,T&B){A^=B^=A^=B;} 16 template<typename T>inline T read(T&x){ 17 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 18 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 19 } 20 const int N=1e5+7; 21 const db eps=1e-7; 22 ll A[N],s[N]; 23 ll L=1,R,mid; 24 int n,l; 25 inline bool check(ll ave){ 26 for(register int i=1;i<l;++i)s[i]=s[i-1]+A[i]-ave; 27 ll minx=1e16; 28 for(register int i=l;i<=n;++i){ 29 MIN(minx,s[i-l]);s[i]=s[i-1]+A[i]-ave; 30 if(s[i]-minx>=0)return 1; 31 } 32 return 0; 33 } 34 35 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout); 36 read(n),read(l); 37 for(register int i=1;i<=n;++i)A[i]=read(A[i])*100000,MAX(R,A[i]); 38 while(L<R){ 39 mid=L+R+1>>1; 40 if(check(mid))L=mid; 41 else R=mid-1; 42 } 43 printf("%lld",(L/100)); 44 return 0; 45 }
做法2:凸包优化
发现以每个点结尾的平均值$ave_i=\frac{S_i-S_j}{i-j}$ $0 \leq j \leq m$
于是想到斜率。问题变成:在前面的区间内找一点与$i$号点连线斜率最大。
然后发现上凸的3个点,中间那个没有用,所以维护一个下凸包。
查找的话是需要二分的,二分找下凸包里斜率$k_{i-1}<k_{i}>k_{i+1}$的这个点。
但是,基于这题并不是让求每个点结尾的最大平均数,而是全局的。
所以有这么一个神仙思路优化复杂度:
在查找时不要二分了,从队首开始比较,若$k_{l,i}<k_{l+1,i}$则弹出队首。
一直到找到这个最大斜率点,作为这个$i$的局部答案。
如果之后出现一个点,他和之前弹出过的点的斜率比目前没有弹出的点间的斜率都要大呢?
是有这种情况的。
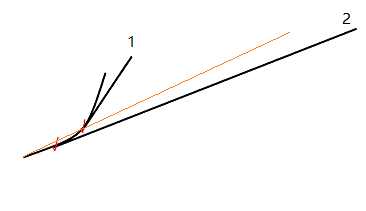
但是,他不会影响全局最优解的形成,即使对于以$i$结尾算错了也没关系。
为什么呢。观察上面这种情况,在1点把下凸包前面一堆全弹掉了。发生这种情况当且仅当这个1号点在橙色线上方。
而2号点那种斜率最大的出现在已经弹出了的点里,必须满足在橙色线下方。
一旦有弹出,那么1号点决策一定比2号点的优。所以2号点算错了也不影响全局最大值。
所以这样的做法是$O(n)$获取全局最优解的。
所以网上说的都是并不严谨的。
这个$O(n)$做法正确性的证明是由hkk神仙提出来的,感谢!大家觉得好可以多去膜他。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define dbg(x) cerr << #x << " = " << x <<endl 7 using namespace std; 8 typedef long long ll; 9 typedef double db; 10 typedef pair<int,int> pii; 11 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 12 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 13 template<typename T>inline char MIN(T&A,T B){return A>B?(A=B,1):0;} 14 template<typename T>inline char MAX(T&A,T B){return A<B?(A=B,1):0;} 15 template<typename T>inline void _swap(T&A,T&B){A^=B^=A^=B;} 16 template<typename T>inline T read(T&x){ 17 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 18 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 19 } 20 const int N=1e5+7; 21 db ans; 22 int n,m; 23 int S[N],q[N],l=1,r; 24 25 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout); 26 read(n),read(m); 27 for(register int i=1;i<=n;++i)S[i]=S[i-1]+read(S[i]); 28 for(register int i=m;i<=n;++i){ 29 while(l<r&&(S[i-m]-S[q[r]])*1ll*(q[r]-q[r-1])<=(S[q[r]]-S[q[r-1]])*1ll*(i-m-q[r]))--r; 30 q[++r]=i-m; 31 while(l<r&&(S[i]-S[q[l]])*1ll*(i-q[l+1])<=(S[i]-S[q[l+1]])*1ll*(i-q[l]))++l; 32 MAX(ans,(db)(S[i]-S[q[l]])/(db)(i-q[l])); 33 } 34 printf("%d\n",(int)(ans*1000)); 35 return 0; 36 }


