poj2750 Potted Flower[线段树]
求一个环待修改最大连续子段和且不能全部选上。
先断环,在$1 \sim n$的链上,考虑没有限制全选的最大连续子段和。显然最大解只有两种情况,一种是这个,一种是另一个。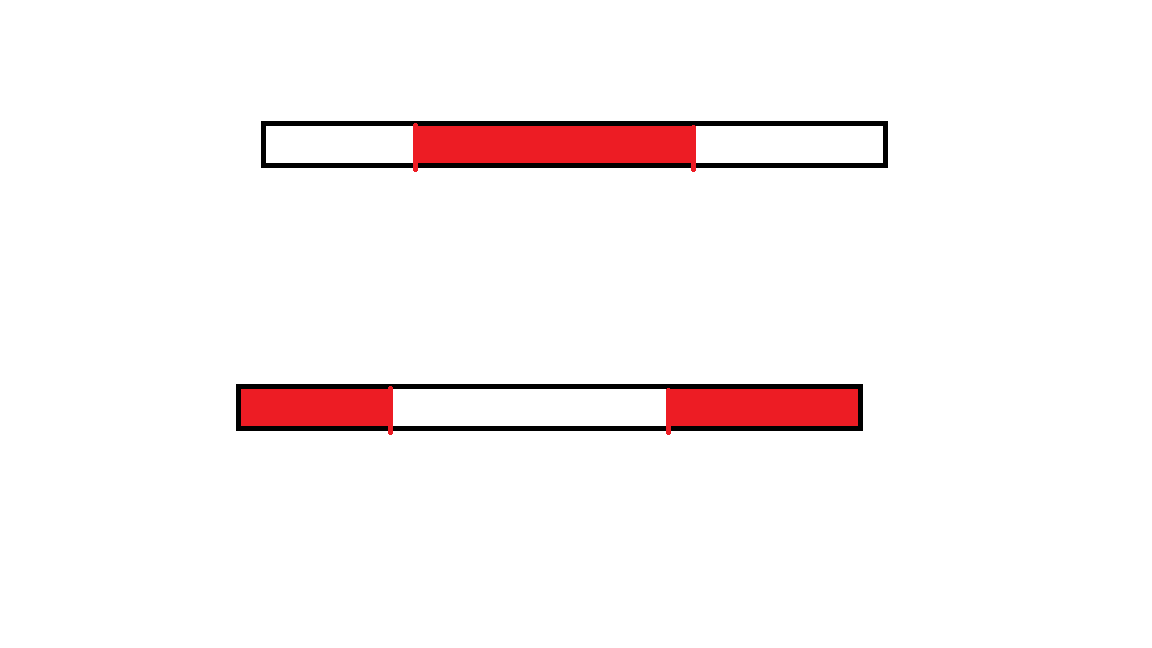
第一个可以直接套路维护,第二个无非就是整体的和减去最小连续子段和。两者取一个最大的就行了。
然后考虑到如果全选的情况。这种情况下只能被迫采取第二种选法。也就是特判若第一种选法等于当前区间和,则强制用第二种(可以证明肯定是对的,且这个其实有漏洞,但是答案不会错)。于是无脑码一波segment_tree即可。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #define dbg(x) cerr<<#x<<" = "<<x<<endl 7 using namespace std; 8 typedef pair<int,int> pii; 9 typedef long long ll; 10 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 11 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 12 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 13 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 14 template<typename T>inline T read(T&x){ 15 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 16 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 17 } 18 const int N=1e5+7; 19 int A[N]; 20 int n,q,x,val; 21 #define lc i<<1 22 #define rc i<<1|1 23 int maxl[N<<2],maxr[N<<2],maxv[N<<2],minl[N<<2],minr[N<<2],minv[N<<2],sumv[N<<2]; 24 inline void Pushup(int i){ 25 maxl[i]=_max(maxl[lc],sumv[lc]+maxl[rc]),maxr[i]=_max(maxr[rc],sumv[rc]+maxr[lc]); 26 minl[i]=_min(minl[lc],sumv[lc]+minl[rc]),minr[i]=_min(minr[rc],sumv[rc]+minr[lc]); 27 maxv[i]=_max(_max(maxv[lc],maxv[rc]),maxr[lc]+maxl[rc]); 28 minv[i]=_min(_min(minv[lc],minv[rc]),minr[lc]+minl[rc]); 29 sumv[i]=sumv[lc]+sumv[rc]; 30 } 31 void build(int i,int L,int R){ 32 if(L==R){maxl[i]=maxr[i]=maxv[i]=minl[i]=minr[i]=minv[i]=sumv[i]=A[L];return;} 33 int mid=L+R>>1;build(lc,L,mid),build(rc,mid+1,R),Pushup(i); 34 } 35 void Update(int i,int L,int R){ 36 if(L==R){maxl[i]=maxr[i]=maxv[i]=minl[i]=minr[i]=minv[i]=sumv[i]=A[L]=val;return;} 37 int mid=L+R>>1;x<=mid?Update(lc,L,mid):Update(rc,mid+1,R);Pushup(i); 38 } 39 40 int main(){//freopen("test.in","r",stdin);freopen("test.out","w",stdout); 41 read(n);for(register int i=1;i<=n;++i)read(A[i]); 42 build(1,1,n); 43 read(q);while(q--){ 44 read(x),read(val); 45 Update(1,1,n); 46 if(maxv[1]==sumv[1])printf("%d\n",sumv[1]-minv[1]); 47 else printf("%d\n",_max(maxv[1],sumv[1]-minv[1])); 48 } 49 return 0; 50 }

