poj1417 True Liars[并查集+背包]
有一点小转化的题,在设计dp状态时还是有点费脑筋的。
地址。
依题意,首先可以知道肯定要扩展域的并查集(明摆着的嘛)。一个"好人"域,一个"坏人"域,每句话分两种情况考虑连边。假设是yes,同域连边,否则异域连边(经典模型嘛)。然后就是要考虑如何验证是否有$x$个好人$y$个坏人的唯一解存在。这取决于联通块。
可以参考我瞎画的图,上面点1~N,下面点N+1~2N。
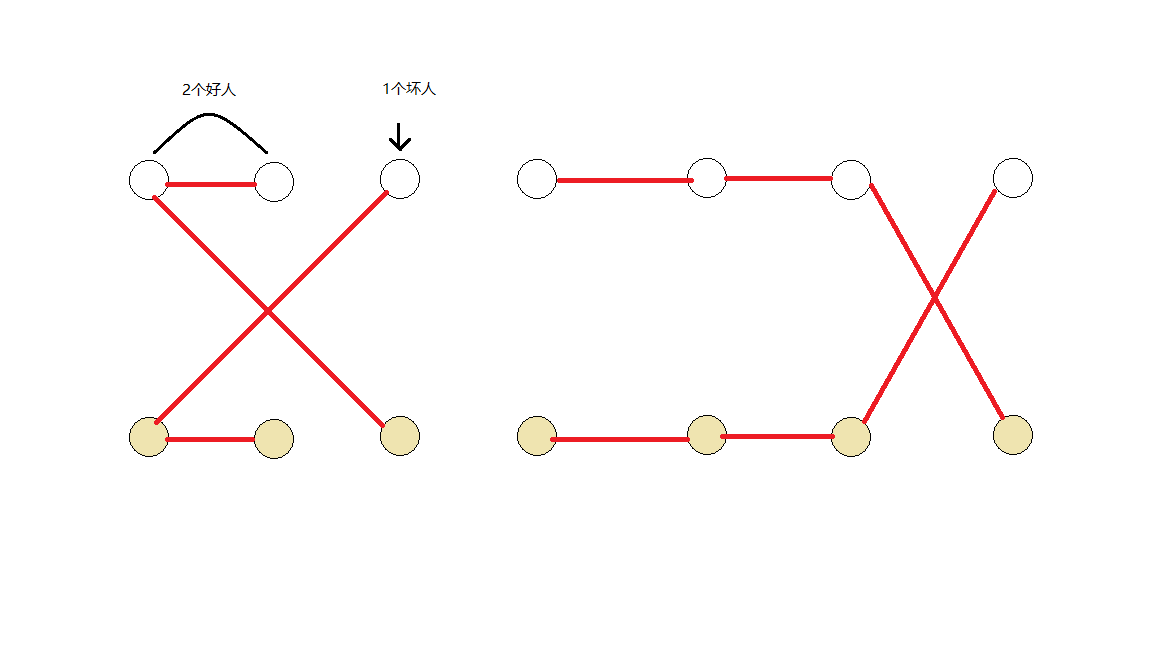
由于并查集合并时操作的对称性,可以发现一个联通块要么$x$个好人$y$个坏人要么$y$个好人$x$个坏人。那么对于所有联通块必须选其中一种方案,最后要凑齐。于是我就想到二维的背包。。但是复杂度太大了啊。。卡了好久,于是又手玩了样例。发现当我所有联通块恰好凑出x个好人时,剩下的不就全是坏人吗。所以只要去做一个好人的背包就行了。dp的时候由于没处理好关于多解的问题,又调了半小时。。一题做两个小时我也是醉了。。其实就是有前面一个状态转移,记一下$pre$。在记一下方案。最终好人的背包装满的状态方案不是1种就是无解,是一种就把所有好人找出来,这个我开了vector存了每个联通块。细节还看code,虽然可能写繁掉了qwq。。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 #include<vector> 8 #define dbg(x) cerr<<#x<<" = "<<x<<endl 9 #define ddbg(x,y) cerr<<#x<<" = "<<x<<" "<<#y<<" = "<<y<<endl 10 using namespace std; 11 typedef long long ll; 12 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 13 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 14 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 15 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 16 template<typename T>inline T read(T&x){ 17 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 18 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 19 } 20 const int N=600+7; 21 int fa[N<<1],f[N][N>>1],cnt[N][N>>1],pos[N],tot,tot2,ans[N]; 22 vector<int> a[N],b[N]; 23 int n,m,gd,bd,x,y; 24 inline int Get(int x){return fa[x]^x?fa[x]=Get(fa[x]):x;} 25 26 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout); 27 while(read(m),read(gd),read(bd),m||gd||bd){ 28 n=gd+bd;char s[5];tot=0,tot2=0;memset(pos,0,sizeof pos); 29 for(register int i=1;i<=n;++i)a[i].clear(),b[i].clear(); 30 for(register int i=1;i<=(n<<1);++i)fa[i]=i; 31 for(register int i=1;i<=m;++i){ 32 read(x),read(y),scanf("%s",s); 33 if(x==y)continue; 34 if(s[0]=='y')fa[Get(x)]=Get(y),fa[Get(x+n)]=Get(y+n); 35 else fa[Get(x)]=Get(y+n),fa[Get(x+n)]=Get(y); 36 } 37 for(register int i=1;i<=n;++i)if(Get(i)<=n)a[Get(i)].push_back(i); 38 for(register int i=n+1;i<=(n<<1);++i)if(Get(i)<=n)b[Get(i)].push_back(i-n); 39 for(register int i=1;i<=n;++i)if(!a[i].empty()||!b[i].empty())pos[++tot]=i;//联通块统计 40 memset(f,0,sizeof f);memset(cnt,0,sizeof cnt);cnt[0][0]=1; 41 for(register int i=1;i<=tot;++i){ 42 x=a[pos[i]].size(),y=b[pos[i]].size(); 43 for(register int j=0,lx=j-x,ly=j-y;j<=gd;++j,lx=j-x,ly=j-y){ 44 if(lx<0&&ly>=0)f[i][j]=ly,cnt[i][j]=cnt[i-1][ly]; 45 else if(lx>=0&&ly<0)f[i][j]=lx,cnt[i][j]=cnt[i-1][lx]; 46 else if(lx>=0&&ly>=0)f[i][j]=cnt[i-1][lx]?lx:ly,cnt[i][j]=cnt[i-1][lx]+cnt[i-1][ly]; 47 } 48 }//做dp 49 if(cnt[tot][gd]^1)printf("no\n"); 50 else{ 51 int j=gd; 52 while(tot){ 53 if(j-f[tot][j]==a[pos[tot]].size()){for(register int i=0;i<a[pos[tot]].size();++i)ans[++tot2]=a[pos[tot]][i];} 54 else for(register int i=0;i<b[pos[tot]].size();++i)ans[++tot2]=b[pos[tot]][i]; 55 j=f[tot--][j]; 56 }//推回去 57 sort(ans+1,ans+tot2+1); 58 for(register int i=1;i<=tot2;++i)printf("%d\n",ans[i]); 59 printf("end\n"); 60 } 61 } 62 return 0; 63 }

